RAC drawing

Last updated
RAC drawings of the complete graph K5 and the complete bipartite graph K3,4 RAC drawings.svg
RAC drawings of the complete graph K5 and the complete bipartite graph K3,4

In graph drawing, a RAC drawing of a graph is a drawing in which the vertices are represented as points, the edges are represented as straight line segments or polylines, at most two edges cross at any point, and when two edges cross they do so at right angles to each other. In the name of this drawing style, "RAC" stands for "right angle crossing".

Contents

The right-angle crossing style and the name "RAC drawing" for this style were both formulated by Didimo, Eades & Liotta (2009), [1] motivated by previous user studies showing that crossings with large angles are much less harmful to the readability of drawings than shallow crossings. [2] Even for planar graphs, allowing some right-angle crossings in a drawing of the graph can significantly improve measures of the drawing quality such as its area or angular resolution. [3]

Examples

The complete graph K5 has a RAC drawing with straight edges, but K6 does not. Every 6-vertex RAC drawing has at most 14 edges, but K6 has 15 edges, too many to have a RAC drawing. [1]

A complete bipartite graph Ka,b has a RAC drawing with straight edges if and only if either min(a,b) ≤ 2 or a + b ≤ 7. If min(a,b) ≤ 2, then the graph is a planar graph, and (by Fáry's theorem) every planar graph has a straight-line drawing with no crossings. Such a drawing is automatically a RAC drawing. The only two cases remaining are the graphs K3,3 and K3,4. A drawing of K3,4 is shown; K3,3 can be formed from it by deleting one vertex. Neither of the next two larger graphs, K4,4 and K3,5, has a RAC drawing. [4]

Edges and bends

If an n-vertex graph (n≥ 4) has a RAC drawing with straight edges, it can have at most 4n − 10 edges. This is tight: there exist RAC-drawable graphs with exactly 4n − 10 edges. [1] For drawings with polyline edges, the bound on the number of edges in the graph depends on the number of bends that are allowed per edge. The graphs that have RAC drawings with one or two bends per edge have O(n) edges; more specifically, with one bend there are at most 5.5n edges [5] and with two bends there are at most 74.2n edges. [6] Every graph has a RAC drawing with three bends per edge. [1]

Relation to 1-planarity

A graph is 1-planar if it has a drawing with at most one crossing per edge. Intuitively, this restriction makes it easier to cause this crossing to be at right angles, and the 4n − 10 bound on the number of edges of straight-line RAC drawings is close to the bounds of 4n − 8 on the number of edges in a 1-planar graph, and of 4n − 9 on the number of edges in a straight-line 1-planar graph. Every RAC drawing with 4n − 10 edges is 1-planar. [7] [8] Additionally, every outer-1-planar graph (that is, a graph drawn with one crossing per edge with all vertices on the outer face of the drawing) has a RAC drawing. [9] However, there exist 1-planar graphs with 4n − 10 edges that do not have RAC drawings. [7]

Computational complexity

It is NP-hard to determine whether a given graph has a RAC drawing with straight edges, [10] even if the input graph is 1-planar and the output RAC drawing must be 1-planar as well. [11] More specifically, RAC drawing is complete for the existential theory of the reals. [12] The RAC drawing problem remains NP-hard for upward drawing of directed acyclic graphs. [13] However, in the special case of outer-1-planar graphs, a RAC drawing can be constructed in linear time. [14]

Related Research Articles

<span class="mw-page-title-main">Graph drawing</span> Visualization of node-link graphs

Graph drawing is an area of mathematics and computer science combining methods from geometric graph theory and information visualization to derive two-dimensional depictions of graphs arising from applications such as social network analysis, cartography, linguistics, and bioinformatics.

<span class="mw-page-title-main">Book embedding</span> Graph layout on multiple half-planes

In graph theory, a book embedding is a generalization of planar embedding of a graph to embeddings in a book, a collection of half-planes all having the same line as their boundary. Usually, the vertices of the graph are required to lie on this boundary line, called the spine, and the edges are required to stay within a single half-plane. The book thickness of a graph is the smallest possible number of half-planes for any book embedding of the graph. Book thickness is also called pagenumber, stacknumber or fixed outerthickness. Book embeddings have also been used to define several other graph invariants including the pagewidth and book crossing number.

<span class="mw-page-title-main">Graph embedding</span> Embedding a graph in a topological space, often Euclidean

In topological graph theory, an embedding of a graph on a surface is a representation of on in which points of are associated with vertices and simple arcs are associated with edges in such a way that:

<span class="mw-page-title-main">Crossing number (graph theory)</span> Fewest edge crossings in drawing of a graph

In graph theory, the crossing numbercr(G) of a graph G is the lowest number of edge crossings of a plane drawing of the graph G. For instance, a graph is planar if and only if its crossing number is zero. Determining the crossing number continues to be of great importance in graph drawing, as user studies have shown that drawing graphs with few crossings makes it easier for people to understand the drawing.

<span class="mw-page-title-main">Layered graph drawing</span> Graph drawing with vertices in horizontal layers

Layered graph drawing or hierarchical graph drawing is a type of graph drawing in which the vertices of a directed graph are drawn in horizontal rows or layers with the edges generally directed downwards. It is also known as Sugiyama-style graph drawing after Kozo Sugiyama, who first developed this drawing style.

<span class="mw-page-title-main">Angular resolution (graph drawing)</span> Sharpest angle between edges at a vertex

In graph drawing, the angular resolution of a drawing of a graph is the sharpest angle formed by any two edges that meet at a common vertex of the drawing.

<span class="mw-page-title-main">Slope number</span> Number of edge slopes in graph drawing

In graph drawing and geometric graph theory, the slope number of a graph is the minimum possible number of distinct slopes of edges in a drawing of the graph in which vertices are represented as points in the Euclidean plane and edges are represented as line segments that do not pass through any non-incident vertex.

<span class="mw-page-title-main">1-planar graph</span>

In topological graph theory, a 1-planar graph is a graph that can be drawn in the Euclidean plane in such a way that each edge has at most one crossing point, where it crosses a single additional edge. If a 1-planar graph, one of the most natural generalizations of planar graphs, is drawn that way, the drawing is called a 1-plane graph or 1-planar embedding of the graph.

In graph drawing, a universal point set of order n is a set S of points in the Euclidean plane with the property that every n-vertex planar graph has a straight-line drawing in which the vertices are all placed at points of S.

<span class="mw-page-title-main">Circular layout</span> Graph drawing with vertices on a circle

In graph drawing, a circular layout is a style of drawing that places the vertices of a graph on a circle, often evenly spaced so that they form the vertices of a regular polygon.

<span class="mw-page-title-main">Arc diagram</span> Graph drawing with vertices on a line

An arc diagram is a style of graph drawing, in which the vertices of a graph are placed along a line in the Euclidean plane, with edges being drawn as semicircles in one or both of the two halfplanes bounded by the line, or as smooth curves formed by sequences of semicircles. In some cases, line segments of the line itself are also allowed as edges, as long as they connect only vertices that are consecutive along the line. Variations of this drawing style in which the semicircles are replaced by convex curves of some other type are also commonly called arc diagrams.

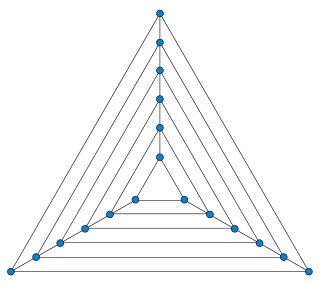
<span class="mw-page-title-main">Nested triangles graph</span> Planar graph used as counterexample

In graph theory, a nested triangles graph with n vertices is a planar graph formed from a sequence of n/3 triangles, by connecting pairs of corresponding vertices on consecutive triangles in the sequence. It can also be formed geometrically, by gluing together n/3 − 1 triangular prisms on their triangular faces. This graph, and graphs closely related to it, have been frequently used in graph drawing to prove lower bounds on the area requirements of various styles of drawings.

In distributed computing and geometric graph theory, greedy embedding is a process of assigning coordinates to the nodes of a telecommunications network in order to allow greedy geographic routing to be used to route messages within the network. Although greedy embedding has been proposed for use in wireless sensor networks, in which the nodes already have positions in physical space, these existing positions may differ from the positions given to them by greedy embedding, which may in some cases be points in a virtual space of a higher dimension, or in a non-Euclidean geometry. In this sense, greedy embedding may be viewed as a form of graph drawing, in which an abstract graph is embedded into a geometric space.

<span class="mw-page-title-main">Upward planar drawing</span> Graph with edges non-crossing and upward

In graph drawing, an upward planar drawing of a directed acyclic graph is an embedding of the graph into the Euclidean plane, in which the edges are represented as non-crossing monotonic upwards curves. That is, the curve representing each edge should have the property that every horizontal line intersects it in at most one point, and no two edges may intersect except at a shared endpoint. In this sense, it is the ideal case for layered graph drawing, a style of graph drawing in which edges are monotonic curves that may cross, but in which crossings are to be minimized.

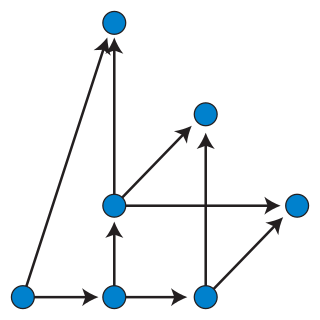
<span class="mw-page-title-main">Dominance drawing</span> Graph where coordinates show reachability

Dominance drawing is a style of graph drawing of directed acyclic graphs that makes the reachability relations between vertices visually apparent. In dominance drawing, vertices are placed at distinct points of the Euclidean plane and a vertex v is reachable from another vertex u if and only if both Cartesian coordinates of v are greater than or equal to the coordinates of u. The edges of a dominance drawing may be drawn either as straight line segments, or, in some cases, as polygonal chains.

In graph theory and graph drawing, a subhamiltonian graph is a subgraph of a planar Hamiltonian graph.

In graph drawing, the area used by a drawing is a commonly used way of measuring its quality.

In graph drawing styles that represent the edges of a graph by polylines, it is desirable to minimize the number of bends per edge or the total number of bends in a drawing. Bend minimization is the algorithmic problem of finding a drawing that minimizes these quantities.

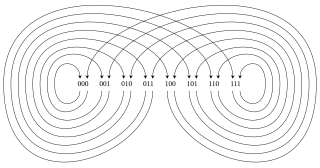
<span class="mw-page-title-main">Queue number</span> Invariant in graph theory

In the mathematical field of graph theory, the queue number of a graph is a graph invariant defined analogously to stack number using first-in first-out (queue) orderings in place of last-in first-out (stack) orderings.

Simultaneous embedding is a technique in graph drawing and information visualization for visualizing two or more different graphs on the same or overlapping sets of labeled vertices, while avoiding crossings within both graphs. Crossings between an edge of one graph and an edge of the other graph are allowed.

References

  1. 1 2 3 4 Didimo, Walter; Eades, Peter; Liotta, Giuseppe (2009), "Drawing graphs with right angle crossings", Algorithms and Data Structures: 11th International Symposium, WADS 2009, Banff, Canada, August 21–23, 2009. Proceedings, Lecture Notes in Computer Science, vol. 5664, pp. 206–217, doi:10.1007/978-3-642-03367-4_19, ISBN   978-3-642-03366-7 .
  2. ↑ Huang, Weidong; Hong, Seok-Hee; Eades, Peter (2008), "Effects of crossing angles", IEEE Pacific Visualization Symposium (PacificVIS '08), pp. 41–46, doi:10.1109/PACIFICVIS.2008.4475457, ISBN   978-1-4244-1966-1 .
  3. ↑ van Kreveld, Marc (2011), "The quality ratio of RAC drawings and planar drawings of planar graphs", Graph Drawing: 18th International Symposium, GD 2010, Konstanz, Germany, September 21–24, 2010, Revised Selected Papers, Lecture Notes in Computer Science, vol. 6502, pp. 371–376, doi: 10.1007/978-3-642-18469-7_34 , ISBN   978-3-642-18468-0 .
  4. ↑ Didimo, Walter; Eades, Peter; Liotta, Giuseppe (2010), "A characterization of complete bipartite RAC graphs", Information Processing Letters , 110 (16): 687–691, doi:10.1016/j.ipl.2010.05.023, MR   2676805 .
  5. ↑ Angelini, Patrizio; Bekos, Michael; Förster, Henry; Kaufmann, Michael (2018), On RAC Drawings of Graphs with one Bend per Edge, arXiv: 1808.10470
  6. ↑ Arikushi, Karin; Fulek, Radoslav; Keszegh, Balázs; Morić, Filip; Tóth, Csaba D. (2012), "Graphs that admit right angle crossing drawings", Computational Geometry Theory & Applications , 45 (4): 169–177, arXiv: 1001.3117 , doi: 10.1016/j.comgeo.2011.11.008 , MR   2876688 .
  7. 1 2 Eades, Peter; Liotta, Giuseppe (2013), "Right angle crossing graphs and 1-planarity", Discrete Applied Mathematics, 161 (7–8): 961–969, doi: 10.1016/j.dam.2012.11.019 , MR   3030582 .
  8. ↑ Ackerman, Eyal (2014), "A note on 1-planar graphs", Discrete Applied Mathematics, 175: 104–108, doi: 10.1016/j.dam.2014.05.025 , MR   3223912 .
  9. ↑ Dehkordi, Hooman Reisi; Eades, Peter (2012), "Every outer-1-plane graph has a right angle crossing drawing", International Journal of Computational Geometry & Applications, 22 (6): 543–557, doi:10.1142/S021819591250015X, MR   3042921 .
  10. ↑ Argyriou, Evmorfia N.; Bekos, Michael A.; Symvonis, Antonios (2011), "The straight-line RAC drawing problem is NP-hard", SOFSEM 2011: 37th Conference on Current Trends in Theory and Practice of Computer Science, Nový Smokovec, Slovakia, January 22-28, 2011, Proceedings, Lecture Notes in Computer Science, vol. 6543, pp. 74–85, arXiv: 1009.5227 , Bibcode:2011LNCS.6543...74A, doi:10.1007/978-3-642-18381-2_6, ISBN   978-3-642-18380-5
  11. ↑ Bekos, Michael A.; Didimo, Walter; Liotta, Giuseppe; Mehrabi, Saeed; Montecchiani, Fabrizio (2017), "On RAC drawings of 1-planar graphs", Theoretical Computer Science , 689: 48–57, arXiv: 1608.08418 , doi:10.1016/j.tcs.2017.05.039
  12. ↑ Schaefer, Marcus (2021), "RAC-drawability is -complete", Proceedings of the 29th International Symposium on Graph Drawing and Network Visualization (GD 2021), arXiv: 2107.11663
  13. ↑ Angelini, Patrizio; Cittadini, Luca; Di Battista, Giuseppe; Didimo, Walter; Frati, Fabrizio; Kaufmann, Michael; Symvonis, Antonios (2010), "On the perspectives opened by right angle crossing drawings", Graph Drawing: 17th International Symposium, GD 2009, Chicago, IL, USA, September 22–25, 2009, Revised Papers, Lecture Notes in Computer Science, vol. 5849, pp. 21–32, doi: 10.1007/978-3-642-11805-0_5 , ISBN   978-3-642-11804-3 .
  14. ↑ Auer, Christopher; Bachmaier, Christian; Brandenburg, Franz J.; Hanauer, Kathrin; Gleißner, Andreas; Neuwirth, Daniel; Reislhuber, Josef (2013), "Recognizing Outer 1-Planar Graphs in Linear Time", Graph Drawing LNCS, Lecture Notes in Computer Science, 8284: 107–118, doi:10.1007/978-3-319-03841-4, ISBN   978-3-319-03840-7
This page is based on this Wikipedia article
Text is available under the CC BY-SA 4.0 license; additional terms may apply.
Images, videos and audio are available under their respective licenses.