In graph drawing, the angular resolution of a drawing of a graph is the sharpest angle formed by any two edges that meet at a common vertex of the drawing.

In graph drawing, the angular resolution of a drawing of a graph is the sharpest angle formed by any two edges that meet at a common vertex of the drawing.
Formann et al. (1993) observed that every straight-line drawing of a graph with maximum degree d has angular resolution at most 2π/d: if v is a vertex of degree d, then the edges incident to v partition the space around v into d wedges with total angle 2π, and the smallest of these wedges must have an angle of at most 2π/d. More strongly, if a graph is d-regular, it must have angular resolution less than , because this is the best resolution that can be achieved for a vertex on the convex hull of the drawing.
As Formann et al. (1993) showed, the largest possible angular resolution of a graph G is closely related to the chromatic number of the square G2, the graph on the same vertex set in which pairs of vertices are connected by an edge whenever their distance in G is at most two. If G2 can be colored with χ colors, then G may be drawn with angular resolution π/χ − ε, for any ε > 0, by assigning distinct colors to the vertices of a regular χ-gon and placing each vertex of G close to the polygon vertex with the same color. Using this construction, they showed that every graph with maximum degree d has a drawing with angular resolution proportional to 1/d2. This bound is close to tight: they used the probabilistic method to prove the existence of graphs with maximum degree d whose drawings all have angular resolution .
Formann et al. (1993) provided an example showing that there exist graphs that do not have a drawing achieving the maximum possible angular resolution; instead, these graphs have a family of drawings whose angular resolutions tend towards some limiting value without reaching it. Specifically, they exhibited an 11-vertex graph that has drawings of angular resolution π/3 − ε for any ε > 0, but that does not have a drawing of angular resolution exactly π/3.
Every tree may be drawn in such a way that the edges are equally spaced around each vertex, a property known as perfect angular resolution. Moreover, if the edges may be freely permuted around each vertex, then such a drawing is possible, without crossings, with all edges unit length or higher, and with the entire drawing fitting within a bounding box of polynomial area. However, if the cyclic ordering of the edges around each vertex is already determined as part of the input to the problem, then achieving perfect angular resolution with no crossings may sometimes require exponential area. [1]
Perfect angular resolution is not always possible for outerplanar graphs, because vertices on the convex hull of the drawing with degree greater than one cannot have their incident edges equally spaced around them. Nonetheless, every outerplanar graph of maximum degree d has an outerplanar drawing with angular resolution proportional to 1/d. [2]
For planar graphs with maximum degree d, the square-coloring technique of Formann et al. (1993) provides a drawing with angular resolution proportional to 1/d, because the square of a planar graph must have chromatic number proportional to d. More precisely, Wegner conjectured in 1977 that the chromatic number of the square of a planar graph is at most , and it is known that the chromatic number is at most . [3] However, the drawings resulting from this technique are generally not planar.
For some planar graphs, the optimal angular resolution of a planar straight-line drawing is O(1/d3), where d is the degree of the graph. [4] Additionally, such a drawing may be forced to use very long edges, longer by an exponential factor than the shortest edges in the drawing. Malitz & Papakostas (1994) used the circle packing theorem and ring lemma to show that every planar graph with maximum degree d has a planar drawing whose angular resolution is at worst an exponential function of d, independent of the number of vertices in the graph.
It is NP-hard to determine whether a given graph of maximum degree d has a drawing with angular resolution 2π/d, even in the special case that d = 4. [5] However, for certain restricted classes of drawings, including drawings of trees in which extending the leaves to infinity produces a convex subdivision of the plane as well as drawings of planar graphs in which each bounded face is a centrally-symmetric polygon, a drawing of optimal angular resolution may be found in polynomial time. [6]
Angular resolution was first defined by Formann et al. (1993).
Although originally defined only for straight-line drawings of graphs, later authors have also investigated the angular resolution of drawings in which the edges are polygonal chains, [7] circular arcs, [8] or spline curves. [9]
The angular resolution of a graph is closely related to its crossing resolution, the angle formed by crossings in a drawing of the graph. In particular, RAC drawing seeks to ensure that these angles are all right angles, the largest crossing angle possible. [10]
In graph theory, a planar graph is a graph that can be embedded in the plane, i.e., it can be drawn on the plane in such a way that its edges intersect only at their endpoints. In other words, it can be drawn in such a way that no edges cross each other. Such a drawing is called a plane graph, or a planar embedding of the graph. A plane graph can be defined as a planar graph with a mapping from every node to a point on a plane, and from every edge to a plane curve on that plane, such that the extreme points of each curve are the points mapped from its end nodes, and all curves are disjoint except on their extreme points.

Graph drawing is an area of mathematics and computer science combining methods from geometric graph theory and information visualization to derive two-dimensional depictions of graphs arising from applications such as social network analysis, cartography, linguistics, and bioinformatics.

In order theory, a Hasse diagram is a type of mathematical diagram used to represent a finite partially ordered set, in the form of a drawing of its transitive reduction. Concretely, for a partially ordered set one represents each element of as a vertex in the plane and draws a line segment or curve that goes upward from one vertex to another vertex whenever covers . These curves may cross each other but must not touch any vertices other than their endpoints. Such a diagram, with labeled vertices, uniquely determines its partial order.

In graph theory, a book embedding is a generalization of planar embedding of a graph to embeddings in a book, a collection of half-planes all having the same line as their boundary. Usually, the vertices of the graph are required to lie on this boundary line, called the spine, and the edges are required to stay within a single half-plane. The book thickness of a graph is the smallest possible number of half-planes for any book embedding of the graph. Book thickness is also called pagenumber, stacknumber or fixed outerthickness. Book embeddings have also been used to define several other graph invariants including the pagewidth and book crossing number.
In graph theory, the planarity testing problem is the algorithmic problem of testing whether a given graph is a planar graph (that is, whether it can be drawn in the plane without edge intersections). This is a well-studied problem in computer science for which many practical algorithms have emerged, many taking advantage of novel data structures. Most of these methods operate in O(n) time (linear time), where n is the number of edges (or vertices) in the graph, which is asymptotically optimal. Rather than just being a single Boolean value, the output of a planarity testing algorithm may be a planar graph embedding, if the graph is planar, or an obstacle to planarity such as a Kuratowski subgraph if it is not.
In polyhedral combinatorics, a branch of mathematics, Steinitz's theorem is a characterization of the undirected graphs formed by the edges and vertices of three-dimensional convex polyhedra: they are exactly the 3-vertex-connected planar graphs. That is, every convex polyhedron forms a 3-connected planar graph, and every 3-connected planar graph can be represented as the graph of a convex polyhedron. For this reason, the 3-connected planar graphs are also known as polyhedral graphs.

In geometric graph theory, a branch of mathematics, a matchstick graph is a graph that can be drawn in the plane in such a way that its edges are line segments with length one that do not cross each other. That is, it is a graph that has an embedding which is simultaneously a unit distance graph and a plane graph. For this reason, matchstick graphs have also been called planar unit-distance graphs. Informally, matchstick graphs can be made by placing noncrossing matchsticks on a flat surface, hence the name.
In graph theory, a k-degenerate graph is an undirected graph in which every subgraph has at least one vertex of degree at most k: that is, some vertex in the subgraph touches k or fewer of the subgraph's edges. The degeneracy of a graph is the smallest value of k for which it is k-degenerate. The degeneracy of a graph is a measure of how sparse it is, and is within a constant factor of other sparsity measures such as the arboricity of a graph.
In theoretical computer science, Baker's technique is a method for designing polynomial-time approximation schemes (PTASs) for problems on planar graphs. It is named after Brenda Baker, who announced it in a 1983 conference and published it in the Journal of the ACM in 1994.

In graph drawing and geometric graph theory, the slope number of a graph is the minimum possible number of distinct slopes of edges in a drawing of the graph in which vertices are represented as points in the Euclidean plane and edges are represented as line segments that do not pass through any non-incident vertex.
In topological graph theory, a 1-planar graph is a graph that can be drawn in the Euclidean plane in such a way that each edge has at most one crossing point, where it crosses a single additional edge. If a 1-planar graph, one of the most natural generalizations of planar graphs, is drawn that way, the drawing is called a 1-plane graph or 1-planar embedding of the graph.
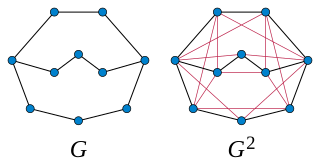
In graph theory, a branch of mathematics, the kth powerGk of an undirected graph G is another graph that has the same set of vertices, but in which two vertices are adjacent when their distance in G is at most k. Powers of graphs are referred to using terminology similar to that of exponentiation of numbers: G2 is called the square of G, G3 is called the cube of G, etc.

In graph drawing, a circular layout is a style of drawing that places the vertices of a graph on a circle, often evenly spaced so that they form the vertices of a regular polygon.

In graph drawing, an upward planar drawing of a directed acyclic graph is an embedding of the graph into the Euclidean plane, in which the edges are represented as non-crossing monotonic upwards curves. That is, the curve representing each edge should have the property that every horizontal line intersects it in at most one point, and no two edges may intersect except at a shared endpoint. In this sense, it is the ideal case for layered graph drawing, a style of graph drawing in which edges are monotonic curves that may cross, but in which crossings are to be minimized.
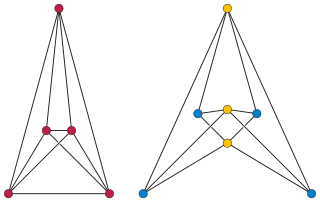
In graph drawing, a RAC drawing of a graph is a drawing in which the vertices are represented as points, the edges are represented as straight line segments or polylines, at most two edges cross at any point, and when two edges cross they do so at right angles to each other. In the name of this drawing style, "RAC" stands for "right angle crossing".
In the mathematical field of graph theory, planarization is a method of extending graph drawing methods from planar graphs to graphs that are not planar, by embedding the non-planar graphs within a larger planar graph.
In graph drawing, the area used by a drawing is a commonly used way of measuring its quality.
In graph drawing styles that represent the edges of a graph by polylines, it is desirable to minimize the number of bends per edge or the total number of bends in a drawing. Bend minimization is the algorithmic problem of finding a drawing that minimizes these quantities.
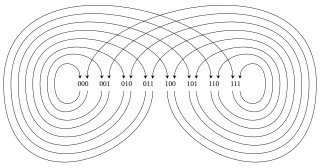
In the mathematical field of graph theory, the queue number of a graph is a graph invariant defined analogously to stack number using first-in first-out (queue) orderings in place of last-in first-out (stack) orderings.
Simultaneous embedding is a technique in graph drawing and information visualization for visualizing two or more different graphs on the same or overlapping sets of labeled vertices, while avoiding crossings within both graphs. Crossings between an edge of one graph and an edge of the other graph are allowed.