Related Research Articles

Molecular diffusion, often simply called diffusion, is the thermal motion of all particles at temperatures above absolute zero. The rate of this movement is a function of temperature, viscosity of the fluid and the size (mass) of the particles. Diffusion explains the net flux of molecules from a region of higher concentration to one of lower concentration. Once the concentrations are equal the molecules continue to move, but since there is no concentration gradient the process of molecular diffusion has ceased and is instead governed by the process of self-diffusion, originating from the random motion of the molecules. The result of diffusion is a gradual mixing of material such that the distribution of molecules is uniform. Since the molecules are still in motion, but an equilibrium has been established, the result of molecular diffusion is called a "dynamic equilibrium". In a phase with uniform temperature, absent external net forces acting on the particles, the diffusion process will eventually result in complete mixing.
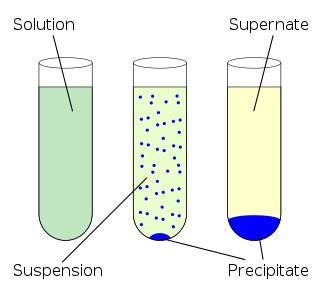
In chemistry, solubility is the ability of a substance, the solute, to form a solution with another substance, the solvent. Insolubility is the opposite property, the inability of the solute to form such a solution.

Molecular dynamics (MD) is a computer simulation method for analyzing the physical movements of atoms and molecules. The atoms and molecules are allowed to interact for a fixed period of time, giving a view of the dynamic "evolution" of the system. In the most common version, the trajectories of atoms and molecules are determined by numerically solving Newton's equations of motion for a system of interacting particles, where forces between the particles and their potential energies are often calculated using interatomic potentials or molecular mechanics force fields. The method is applied mostly in chemical physics, materials science, and biophysics.
In the physical sciences, a partition coefficient (P) or distribution coefficient (D) is the ratio of concentrations of a compound in a mixture of two immiscible solvents at equilibrium. This ratio is therefore a comparison of the solubilities of the solute in these two liquids. The partition coefficient generally refers to the concentration ratio of un-ionized species of compound, whereas the distribution coefficient refers to the concentration ratio of all species of the compound.
A chaotropic agent is a molecule in water solution that can disrupt the hydrogen bonding network between water molecules. This has an effect on the stability of the native state of other molecules in the solution, mainly macromolecules by weakening the hydrophobic effect. For example, a chaotropic agent reduces the amount of order in the structure of a protein formed by water molecules, both in the bulk and the hydration shells around hydrophobic amino acids, and may cause its denaturation.

Malate dehydrogenase (EC 1.1.1.37) (MDH) is an enzyme that reversibly catalyzes the oxidation of malate to oxaloacetate using the reduction of NAD+ to NADH. This reaction is part of many metabolic pathways, including the citric acid cycle. Other malate dehydrogenases, which have other EC numbers and catalyze other reactions oxidizing malate, have qualified names like malate dehydrogenase (NADP+).
Co-solvents are defined as kosmotropic (order-making) if they contribute to the stability and structure of water-water interactions. In contrast, chaotropic (disorder-making) agents have the opposite effect, disrupting water structure, increasing the solubility of nonpolar solvent particles, and destabilizing solute aggregates. Kosmotropes cause water molecules to favorably interact, which in effect stabilizes intramolecular interactions in macromolecules such as proteins.
John "Jack" Gamble Kirkwood was a noted chemist and physicist, holding faculty positions at Cornell University, the University of Chicago, California Institute of Technology, and Yale University.
Implicit solvation is a method to represent solvent as a continuous medium instead of individual “explicit” solvent molecules, most often used in molecular dynamics simulations and in other applications of molecular mechanics. The method is often applied to estimate free energy of solute-solvent interactions in structural and chemical processes, such as folding or conformational transitions of proteins, DNA, RNA, and polysaccharides, association of biological macromolecules with ligands, or transport of drugs across biological membranes.
The Debye–Hückel theory was proposed by Peter Debye and Erich Hückel as a theoretical explanation for departures from ideality in solutions of electrolytes and plasmas. It is a linearized Poisson–Boltzmann model, which assumes an extremely simplified model of electrolyte solution but nevertheless gave accurate predictions of mean activity coefficients for ions in dilute solution. The Debye–Hückel equation provides a starting point for modern treatments of non-ideality of electrolyte solutions.
In a polymer solution, a theta solvent is a solvent in which polymer coils act like ideal chains, assuming exactly their random walk coil dimensions. Therefore, the Mark–Houwink equation exponent is in a theta solvent. Thermodynamically, the excess chemical potential of mixing between a polymer and a theta solvent is zero.
A model lipid bilayer is any bilayer assembled in vitro, as opposed to the bilayer of natural cell membranes or covering various sub-cellular structures like the nucleus. They are used to study the fundamental properties of biological membranes in a simplified and well-controlled environment, and increasingly in bottom-up synthetic biology for the construction of artificial cells. A model bilayer can be made with either synthetic or natural lipids. The simplest model systems contain only a single pure synthetic lipid. More physiologically relevant model bilayers can be made with mixtures of several synthetic or natural lipids.
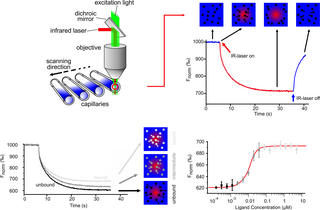
Microscale thermophoresis (MST) is a technology for the biophysical analysis of interactions between biomolecules. Microscale thermophoresis is based on the detection of a temperature-induced change in fluorescence of a target as a function of the concentration of a non-fluorescent ligand. The observed change in fluorescence is based on two distinct effects. On the one hand it is based on a temperature related intensity change (TRIC) of the fluorescent probe, which can be affected by binding events. On the other hand, it is based on thermophoresis, the directed movement of particles in a microscopic temperature gradient. Any change of the chemical microenvironment of the fluorescent probe, as well as changes in the hydration shell of biomolecules result in a relative change of the fluorescence detected when a temperature gradient is applied and can be used to determine binding affinities. MST allows measurement of interactions directly in solution without the need of immobilization to a surface.
Pitzer equations are important for the understanding of the behaviour of ions dissolved in natural waters such as rivers, lakes and sea-water. They were first described by physical chemist Kenneth Pitzer. The parameters of the Pitzer equations are linear combinations of parameters, of a virial expansion of the excess Gibbs free energy, which characterise interactions amongst ions and solvent. The derivation is thermodynamically rigorous at a given level of expansion. The parameters may be derived from various experimental data such as the osmotic coefficient, mixed ion activity coefficients, and salt solubility. They can be used to calculate mixed ion activity coefficients and water activities in solutions of high ionic strength for which the Debye–Hückel theory is no longer adequate. They are more rigorous than the equations of specific ion interaction theory, but Pitzer parameters are more difficult to determine experimentally than SIT parameters.
Binding selectivity is defined with respect to the binding of ligands to a substrate forming a complex. Binding selectivity describes how a ligand may bind more preferentially to one receptor than another. A selectivity coefficient is the equilibrium constant for the reaction of displacement by one ligand of another ligand in a complex with the substrate. Binding selectivity is of major importance in biochemistry and in chemical separation processes.
Salting in refers to the effect where increasing the ionic strength of a solution increases the solubility of a solute, such as a protein. This effect tends to be observed at lower ionic strengths. Protein solubility is a complex function of physicochemical nature of the protein, pH, temperature, and the concentration of the salt used. It also depends on whether the salt is kosmotropic, whereby the salt will stabilize water. The solubility of proteins usually increases slightly in the presence of salt, referred to as "salting in". However, at high concentrations of salt, the solubility of the proteins drop sharply and proteins can precipitate out, referred to as "salting out".
The Kirkwood–Buff (KB) solution theory, due to John G. Kirkwood and Frank P. Buff, links macroscopic (bulk) properties to microscopic (molecular) details. Using statistical mechanics, the KB theory derives thermodynamic quantities from pair correlation functions between all molecules in a multi-component solution. The KB theory proves to be a valuable tool for validation of molecular simulations, as well as for the molecular-resolution elucidation of the mechanisms underlying various physical processes. For example, it has numerous applications in biologically relevant systems.
Kinetic theory may refer to:
In chemistry, cosolvents are substances added to a primary solvent in small amounts to increase the solubility of a poorly-soluble compound. Their use is most prevalent in chemical and biological research relating to pharmaceuticals and food science, where alcohols are frequently used as cosolvents in water to dissolve hydrophobic molecules during extraction, screening, and formulation. Cosolvents find applications also in environmental chemistry and are known as effective countermeasures against pollutant non-aqueous phase liquids, as well as in the production of functional energy materials and synthesis of biodiesel.
Nico van der Vegt is a Dutch chemist and a professor for computational physical chemistry at Technische Universität Darmstadt
References
- ↑ Schurr JM, Rangel DP, Aragon SR. (2005) "A Contribution to the Theory of Preferential Interaction Coefficients." Archived October 11, 2007, at the Wayback Machine Biophysical Journal.89:2258-2276.
- ↑ Shulgin IL, Ruckenstein E (2006) "A Protein Molecule in a Mixed Solvent: The Preferential Binding Parameter via the Kirkwood-Buff theory." Biophysical Journal.90:704–707.
- ↑ Pierce V, Kang M, Weerasinghe S, Smith PE. (2008) "Recent Applications of Kirkwood-Buff Theory to Biological Systems." Cell Biochem Biophys.50(1):1-22.
- ↑ Thomas Record Jr. M, Anderson CF. (1995) "Interpretation of Preferential Interaction Coefficients of Nonelectrolytes and of Electrolyte Ions in Terms of a Two-Domain Model." Biophysical Journal.68:786-794.