Bjerknes force

Last updated December 14, 2023

Bjerknes forces are translational forces on bubbles in a sound wave. The phenomenon is a type of acoustic radiation force. Primary Bjerknes forces are caused by an external sound field; secondary Bjerknes forces are attractive or repulsive forces between pairs of bubbles in the same sound field caused by the pressure field generated by each bubble volume's oscillations. They were first described by Vilhelm Bjerknes in his 1906 Fields of Force.^[1]

Hydrodynamics – electromagnetism analogy

In Fields of Force Bjerknes lay out geometrical and dynamical analogies between the Maxwell's theory of electromagnetism and hydrodynamics. In the light of these analogies the Bjerknes forces are being predicted.

Principle of kinematic buoyancy

Bjerknes writes:

"Any body which participates in the translatory motion of a fluid mass is subject to a kinematic buoyancy equal to the product of the acceleration of the translatory motion multiplied by the mass of the water displaced by the body"^[1]

This principle is analogous to Archimedes' principle. Based on this principle the force acting on a particle of volume $V$ is $F={\mathbf {a}}\rho V={\frac {\partial {\mathbf {u}}}{\partial t}}\rho V$ .^[2] Where ${\mathbf {u}}$ is the fluid velocity and $\rho$ is the fluid density.

Using conservation of momentum for incompressible non-viscous fluid one can find that to first order: $\rho {\frac {\partial {\mathbf {u}}}{\partial t}}=-\nabla P$ ,^[2] Concluding that $F=-V\nabla P$ .

Charge and oscillating particles

Bjerknes realized that the velocity field generated by an expanding particle in an incompressible fluid has the same geometrical structure as the electric field generated by a positively charged particle, and that the same applies for contracting particle and a negatively charged particle.

In the case of an oscillating motion, Bjerknes argued that two particles that oscillate in phase generate a velocity field that is geometrically equivalent to the electric field generated by two particles with the same charge, whereas two particles that oscillate in an opposite phase will generate a velocity field that is geometrically equivalent to the electric field generated by particles with an opposite sign.

Bjerknes then writes:

"Between Bodies pulsating in the same phase there is an apparent attraction; between bodies pulsating in the opposite phase there is an apparent repulsion, the force being proportional to the product of the two intensities of pulsating, and proportional to the inverse square of the distance."^[1]

This result is counter to our intuition, as it demonstrates that bodies oscillating in phase exert an attractive force on each other, despite creating a field akin to that of identically charged particles. This result was described by Bjerknes as "Astonishing".^[1]

Primary Bjerknes force

The force on a small particle in a sound wave is given by:

F=-V\nabla P

where V is the volume of the particle, and $\nabla$ P is the acoustic pressure gradient on the bubble.

Assuming a sinusoidal standing wave,^[3] the time-averaged pressure gradient over a single acoustic cycle is zero, meaning a solid particle (with fixed volume) experiences no net force. However, because a bubble is compressible, the oscillating pressure field also causes its volume to change; for spherical bubbles this can be described by the Rayleigh–Plesset equation. This means the time-averaged product of the bubble volume and the pressure gradient can be non-zero over an acoustic cycle. Unlike acoustic radiation forces on incompressible particles, net forces can be generated in the absence of attenuation or reflection of the sound wave.

The sign of the force will depend on the relative phase between the pressure field $P(t)$ and the volume $V(t)$ oscillations.^[3] According to the theory of forced harmonic oscillator the relative phase will depend on the difference between the bubble resonant frequency and the acoustic driving frequency.

Bubble focusing

From Rayleigh–Plesset equation one can derive the bubble resonant frequency:^[4]

$\omega _{0}^{2}={\frac {1}{\rho R_{0}^{2}}}{\Bigl (}3\kappa {\bigl (}P_{0}-P_{V}{\bigr )}+2(3\kappa -1){\frac {\sigma }{R_{0}}}{\Bigr )}$

Where $\rho$ is the fluid density, $R_{0}$ is the rest radius of the bubble, $\kappa$ is the polytropic index, $P_{0}$ is the ambient pressure, $P_{V}$ is the vapor pressure and $\sigma$ is the surface tension constant.

Bubbles with resonance frequency above the acoustic driving frequency travel up the pressure gradient, while those with a lower resonance frequency travel down the pressure gradient.^[3]

The dependence of the resonant frequency ( $\omega _{0}$ ) on the rest radius of the bubble predicts that for standing waves, there is a critical radius $R_{c}$ that depends on the driving frequency. Small bubbles ( $R_{0}<R_{c}$ ) accumulate at pressure antinodes, whereas large bubbles ( $R_{0}>R_{c}$ ) accumulate at pressure nodes.^[3]

Related Research Articles

In physics, physical chemistry and engineering, fluid dynamics is a subdiscipline of fluid mechanics that describes the flow of fluids—liquids and gases. It has several subdisciplines, including aerodynamics and hydrodynamics. Fluid dynamics has a wide range of applications, including calculating forces and moments on aircraft, determining the mass flow rate of petroleum through pipelines, predicting weather patterns, understanding nebulae in interstellar space and modelling fission weapon detonation.

The vorticity equation of fluid dynamics describes the evolution of the vorticity $ω$ of a particle of a fluid as it moves with its flow; that is, the local rotation of the fluid. The governing equation is:

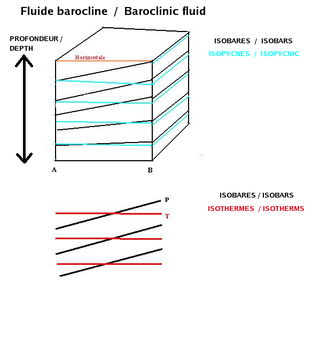
In fluid dynamics, the baroclinity of a stratified fluid is a measure of how misaligned the gradient of pressure is from the gradient of density in a fluid. In meteorology a baroclinic flow is one in which the density depends on both temperature and pressure. A simpler case, barotropic flow, allows for density dependence only on pressure, so that the curl of the pressure-gradient force vanishes.

In fluid dynamics, Stokes' law is an empirical law for the frictional force – also called drag force – exerted on spherical objects with very small Reynolds numbers in a viscous fluid. It was derived by George Gabriel Stokes in 1851 by solving the Stokes flow limit for small Reynolds numbers of the Navier–Stokes equations.

In fluid dynamics, the Euler equations are a set of quasilinear partial differential equations governing adiabatic and inviscid flow. They are named after Leonhard Euler. In particular, they correspond to the Navier–Stokes equations with zero viscosity and zero thermal conductivity.

In fluid mechanics, or more generally continuum mechanics, incompressible flow refers to a flow in which the material density is constant within a fluid parcel—an infinitesimal volume that moves with the flow velocity. An equivalent statement that implies incompressibility is that the divergence of the flow velocity is zero.

<span class="mw-page-title-main">Smoothed-particle hydrodynamics</span> Method of hydrodynamics simulation

Smoothed-particle hydrodynamics (SPH) is a computational method used for simulating the mechanics of continuum media, such as solid mechanics and fluid flows. It was developed by Gingold and Monaghan and Lucy in 1977, initially for astrophysical problems. It has been used in many fields of research, including astrophysics, ballistics, volcanology, and oceanography. It is a meshfree Lagrangian method, and the resolution of the method can easily be adjusted with respect to variables such as density.

Stokes flow, also named creeping flow or creeping motion, is a type of fluid flow where advective inertial forces are small compared with viscous forces. The Reynolds number is low, i.e. $. This is a typical situation in flows where the fluid velocities are very slow, the viscosities are very large, or the length-scales of the flow are very small. Creeping flow was first studied to understand lubrication. In nature, this type of flow occurs in the swimming of microorganisms and sperm. In technology, it occurs in paint, MEMS devices, and in the flow of viscous polymers generally.$

Aeroacoustics is a branch of acoustics that studies noise generation via either turbulent fluid motion or aerodynamic forces interacting with surfaces. Noise generation can also be associated with periodically varying flows. A notable example of this phenomenon is the Aeolian tones produced by wind blowing over fixed objects.

In physics, the acoustic wave equation is a second-order partial differential equation that governs the propagation of acoustic waves through a material medium resp. a standing wavefield. The equation describes the evolution of acoustic pressure $p$ or particle velocity $u$ as a function of position $x$ and time $t$ . A simplified (scalar) form of the equation describes acoustic waves in only one spatial dimension, while a more general form describes waves in three dimensions. Propagating waves in a pre-defined direction can also be calculated using first order one-way wave equation.

In physics, magnetic pressure is an energy density associated with a magnetic field. In SI units, the energy density $of a magnetic field with strength can be expressed as$

In fluid dynamics, dynamic pressure is the quantity defined by:

The intent of this article is to highlight the important points of the derivation of the Navier–Stokes equations as well as its application and formulation for different families of fluids.

Pressure-correction method is a class of methods used in computational fluid dynamics for numerically solving the Navier-Stokes equations normally for incompressible flows.

Volume viscosity is a material property relevant for characterizing fluid flow. Common symbols are $or . It has dimensions, and the corresponding SI unit is the pascal-second (Pa\cdots).$

The Cauchy momentum equation is a vector partial differential equation put forth by Cauchy that describes the non-relativistic momentum transport in any continuum.

In fluid dynamics, Airy wave theory gives a linearised description of the propagation of gravity waves on the surface of a homogeneous fluid layer. The theory assumes that the fluid layer has a uniform mean depth, and that the fluid flow is inviscid, incompressible and irrotational. This theory was first published, in correct form, by George Biddell Airy in the 19th century.

Acoustic radiation force (ARF) is a physical phenomenon resulting from the interaction of an acoustic wave with an obstacle placed along its path. Generally, the force exerted on the obstacle is evaluated by integrating the acoustic radiation pressure over its time-varying surface.

The multiphase particle-in-cell method (MP-PIC) is a numerical method for modeling particle-fluid and particle-particle interactions in a computational fluid dynamics (CFD) calculation. The MP-PIC method achieves greater stability than its particle-in-cell predecessor by simultaneously treating the solid particles as computational particles and as a continuum. In the MP-PIC approach, the particle properties are mapped from the Lagrangian coordinates to an Eulerian grid through the use of interpolation functions. After evaluation of the continuum derivative terms, the particle properties are mapped back to the individual particles. This method has proven to be stable in dense particle flows, computationally efficient, and physically accurate. This has allowed the MP-PIC method to be used as particle-flow solver for the simulation of industrial-scale chemical processes involving particle-fluid flows.

Acoustic tweezers are a set of tools that use sound waves to manipulate the position and movement of very small objects. Strictly speaking, only a single-beam based configuration can be called acoustical tweezers. However, the broad concept of acoustical tweezers involves two configurations of beams: single beam and standing waves. The technology works by controlling the position of acoustic pressure nodes that draw objects to specific locations of a standing acoustic field. The target object must be considerably smaller than the wavelength of sound used, and the technology is typically used to manipulate microscopic particles.

References

1 2 3 4 Bjerknes, V. (1906). Fields of force. General Books.
1 2 Crum, Lawrence A. (1975-06-01). "Bjerknes forces on bubbles in a stationary sound field". The Journal of the Acoustical Society of America. 57 (6): 1363–1370. doi:10.1121/1.380614. ISSN 0001-4966.
1 2 3 4 Leighton, T.G., Walton, A.J. and Pickworth, M.J.W., 1990. Primary bjerknes forces. European Journal of Physics, 11(1), p.47.
↑ Brennen, Christopher Earls (2013-10-14). Cavitation and Bubble Dynamics (1 ed.). Cambridge University Press. doi:10.1017/cbo9781107338760. ISBN 978-1-107-64476-2.

External links

Ball, Philip (2022-06-24). "Manipulating Objects Using Air Bubbles and Sound Waves". Physics. 15. doi: 10.1103/Physics.15.92 . S2CID 251084556.

This page is based on this Wikipedia article
Text is available under the CC BY-SA 4.0 license; additional terms may apply.
Images, videos and audio are available under their respective licenses.

[:0-1] 1 2 3 4 Bjerknes, V. (1906). Fields of force. General Books.

[:1-2] 1 2 Crum, Lawrence A. (1975-06-01). "Bjerknes forces on bubbles in a stationary sound field". The Journal of the Acoustical Society of America. 57 (6): 1363–1370. doi:10.1121/1.380614. ISSN 0001-4966.

[:2-3] 1 2 3 4 Leighton, T.G., Walton, A.J. and Pickworth, M.J.W., 1990. Primary bjerknes forces. European Journal of Physics, 11(1), p.47.

[4] Brennen, Christopher Earls (2013-10-14). Cavitation and Bubble Dynamics (1 ed.). Cambridge University Press. doi:10.1017/cbo9781107338760. ISBN 978-1-107-64476-2.

[1]

[2]

[3]

[4]