
Multiplication is one of the four elementary mathematical operations of arithmetic, with the other ones being addition, subtraction, and division. The result of a multiplication operation is called a product.

In radio communications, single-sideband modulation (SSB) or single-sideband suppressed-carrier modulation (SSB-SC) is a type of modulation used to transmit information, such as an audio signal, by radio waves. A refinement of amplitude modulation, it uses transmitter power and bandwidth more efficiently. Amplitude modulation produces an output signal the bandwidth of which is twice the maximum frequency of the original baseband signal. Single-sideband modulation avoids this bandwidth increase, and the power wasted on a carrier, at the cost of increased device complexity and more difficult tuning at the receiver.

In physics and mechanics, torque is the rotational equivalent of linear force. It is also referred to as the moment, moment of force, rotational force or turning effect, depending on the field of study. It represents the capability of a force to produce change in the rotational motion of the body. The concept originated with the studies by Archimedes of the usage of levers. Just as a linear force is a push or a pull, a torque can be thought of as a twist to an object around a specific axis. Torque is defined as the product of the magnitude of the force and the perpendicular distance of the line of action of a force from the axis of rotation. The symbol for torque is typically , the lowercase Greek letter tau. When being referred to as moment of force, it is commonly denoted by M.
The jansky is a non-SI unit of spectral flux density, or spectral irradiance, used especially in radio astronomy. It is equivalent to 10−26 watts per square metre per hertz.
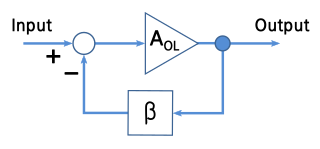
A Negative-feedback amplifier is an electronic amplifier that subtracts a fraction of its output from its input, so that negative feedback opposes the original signal. The applied negative feedback can improve its performance and reduces sensitivity to parameter variations due to manufacturing or environment. Because of these advantages, many amplifiers and control systems use negative feedback.
In fluid dynamics, the Darcy–Weisbach equation is an empirical equation that relates the head loss, or pressure loss, due to friction along a given length of pipe to the average velocity of the fluid flow for an incompressible fluid. The equation is named after Henry Darcy and Julius Weisbach. Currently, there is no formula more accurate or universally applicable than the Darcy-Weisbach supplemented by the Moody diagram or Colebrook equation.
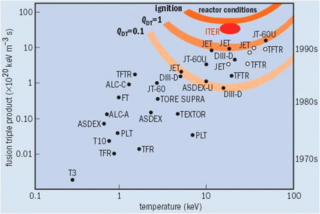
The Lawson criterion is a figure of merit used in nuclear fusion research. It compares the rate of energy being generated by fusion reactions within the fusion fuel to the rate of energy losses to the environment. When the rate of production is higher than the rate of loss, the system will produce net energy. If enough of that energy is captured by the fuel, the system will become self-sustaining and is said to be ignited.

In machine learning, backpropagation is a widely used algorithm for training feedforward neural networks. Generalizations of backpropagation exist for other artificial neural networks (ANNs), and for functions generally. These classes of algorithms are all referred to generically as "backpropagation". In fitting a neural network, backpropagation computes the gradient of the loss function with respect to the weights of the network for a single input–output example, and does so efficiently, unlike a naive direct computation of the gradient with respect to each weight individually. This efficiency makes it feasible to use gradient methods for training multilayer networks, updating weights to minimize loss; gradient descent, or variants such as stochastic gradient descent, are commonly used. The backpropagation algorithm works by computing the gradient of the loss function with respect to each weight by the chain rule, computing the gradient one layer at a time, iterating backward from the last layer to avoid redundant calculations of intermediate terms in the chain rule; this is an example of dynamic programming.
The heat transfer coefficient or film coefficient, or film effectiveness, in thermodynamics and in mechanics is the proportionality constant between the heat flux and the thermodynamic driving force for the flow of heat :
The urea reduction ratio (URR) is a dimensionless number used to quantify dialysis treatment adequacy.
In the insurance industry in the United States, an experience modifier or experience modification is an adjustment of an employer's premium for worker's compensation coverage based on the losses the insurer has experienced from that employer. An experience modifier of 1 would be applied for an employer that had demonstrated the actuarially expected performance. Poorer loss experience leads to a modifier greater than 1, and better experience to a modifier less than 1. The loss experience used in determining the modifier typically comprises three years but excluding the immediate past year. For instance, if a policy expired on January 1, 2018, the period reflected by the experience modifier would run from January 1, 2014 to January 1, 2017.
Loss reserving refers to the calculation of the required reserves for a tranche of general insurance business. It includes outstanding claims reserves.
In insurance, incurred but not reported (IBNR) claims is the amount owed by an insurer to all valid claimants who have had a covered loss but have not yet reported it. Since the insurer knows neither how many of these losses have occurred, nor the severity of each loss, IBNR is necessarily an estimate. The sum of IBNR losses plus reported losses yields an estimate of the total eventual liabilities the insurer will cover, known as ultimate losses.
In competition law, before deciding whether companies have significant market power which would justify government intervention, the test of small but significant and non-transitory increase in price (SSNIP) is used to define the relevant market in a consistent way. It is an alternative to ad hoc determination of the relevant market by arguments about product similarity.
In convective heat transfer, the Churchill–Bernstein equation is used to estimate the surface averaged Nusselt number for a cylinder in cross flow at various velocities. The need for the equation arises from the inability to solve the Navier–Stokes equations in the turbulent flow regime, even for a Newtonian fluid. When the concentration and temperature profiles are independent of one another, the mass-heat transfer analogy can be employed. In the mass-heat transfer analogy, heat transfer dimensionless quantities are replaced with analogous mass transfer dimensionless quantities.
Ranking of query is one of the fundamental problems in information retrieval (IR), the scientific/engineering discipline behind search engines. Given a query q and a collection D of documents that match the query, the problem is to rank, that is, sort, the documents in D according to some criterion so that the "best" results appear early in the result list displayed to the user. Ranking in terms of information retrieval is an important concept in computer science and is used in many different applications such as search engine queries and recommender systems. A majority of search engines use ranking algorithms to provide users with accurate and relevant results.
In statistics, L-moments are a sequence of statistics used to summarize the shape of a probability distribution. They are linear combinations of order statistics (L-statistics) analogous to conventional moments, and can be used to calculate quantities analogous to standard deviation, skewness and kurtosis, termed the L-scale, L-skewness and L-kurtosis respectively. Standardised L-moments are called L-moment ratios and are analogous to standardized moments. Just as for conventional moments, a theoretical distribution has a set of population L-moments. Sample L-moments can be defined for a sample from the population, and can be used as estimators of the population L-moments.
A logarithmic resistor ladder is an electronic circuit composed of a series of resistors and switches, designed to create an attenuation from an input to an output signal, where the logarithm of the attenuation ratio is proportional to a digital code word that represents the state of the switches.
The chain-ladder or development method is a prominent actuarial loss reserving technique. The chain-ladder method is used in both the property and casualty and health insurance fields. Its intent is to estimate incurred but not reported claims and project ultimate loss amounts. The primary underlying assumption of the chain-ladder method is that historical loss development patterns are indicative of future loss development patterns.
Loss development factors or LDFs are used in insurance pricing and reserving to adjust claims to their projected ultimate level. Insurance claims, especially in long-tailed lines such as liability insurance, are often not paid out immediately. Claims adjusters set initial case reserves for claims; however, it is often impossible to predict immediately what the final amount of an insurance claim will be, due to uncertainty around defense costs, settlement amounts, and trial outcomes. Loss development factors are used by actuaries, underwriters, and other insurance professionals to "develop" claim amounts to their estimated final value. Ultimate loss amounts are necessary for determining an insurance company's carried reserves. They are also useful for determining adequate insurance premiums, when loss experience is used as a rating factor







