Brian Alspach

Last updated

Brian Roger Alspach is a mathematician whose main research interest is in graph theory. Alspach has also studied the mathematics behind poker, and writes for Poker Digest and Canadian Poker Player magazines.

Contents

Biography

Brian Alspach was born on May 29, 1938, in North Dakota. He attended the University of Washington from 1957 to 1961, receiving his B.A. in 1961. He taught at a junior high school for one year before beginning his graduate studies. In 1964 he received his master's degree and in 1966 he obtained his Ph.D. from the University of California, Santa Barbara under the supervision of Paul Kelly. [1] He taught at Simon Fraser University for 33 years. He retired from there in 1998. He currently works as an adjunct professor at the University of Regina and has been there since 1999. He is responsible for creating an industrial mathematics degree at Simon Fraser University. [2]

Brian Alspach believes that the growth and future of mathematics will depend on the business people in the industrial businesses. [2] His interests are in graph theory and its applications. One of his theories of coverings and decomposition has been applied to scheduling issues that can arise in the business world. Alspach states that his biggest issue with this is trying to explain such complex math to people in the business world with only a basic understanding of math. He has mentored a total of 13 Ph.D. students. His wife is the former vice president of academics at the University of Regina where he was an adjunct professor. [3] Brian is currently employed as conjoint professor at the University of Newcastle. [4]

Research

One of his first publications was an article titled Cycles of each length in regular tournaments, which was published in the Canadian Mathematical Bulletin (November, 1967). [5]

Another influential piece of Brian Alspach is Point-symmetric graphs and digraphs of prime order and transitive permutation groups of prime degree, which was published in the Journal of Combinatorial Theory (August, 1973). [6]

In his article titled Isomorphism of circulant graphs and digraphs which was published in Discrete Mathematics (February, 1979). [7] He discusses the isomorphism problem for a special class of graphs.

Brian Alspach coauthored an article with T. D. Parsons titled A construction for vertex –transitive graph published in the Canadian Journal of Mathematics (April, 1982). [8]

Cycle double cover conjecture is one of the major open problems in graph theory. This conjecture was solved by Brian Alspach and Cun-Quan Zhang for the family of Petersen-minor free graph [9]

Alspach's conjecture, posed by Alspach in 1981, concerns the characterization of disjoint cycle covers of complete graphs with prescribed cycle lengths. With Heather Gavlas Jordon, in 2001, Alspach proved a special case, on the decomposition of complete graphs into cycles that all have the same length. This is possible if and only if the complete graph has an odd number of vertices (so its degree is even), the given cycle length is at most the number of vertices (so that cycles of that length exist), and the given length divides the number of edges of the graph. [10] A proof of the full conjecture was published in 2014. [11]

Related Research Articles

<span class="mw-page-title-main">Dragan Marušič</span> Slovenian mathematician

Dragan Marušič is a Slovene mathematician. Marušič obtained his BSc in technical mathematics from the University of Ljubljana in 1976, and his PhD from the University of Reading in 1981 under the supervision of Crispin Nash-Williams.

<span class="mw-page-title-main">Petersen graph</span> Cubic graph with 10 vertices and 15 edges

In the mathematical field of graph theory, the Petersen graph is an undirected graph with 10 vertices and 15 edges. It is a small graph that serves as a useful example and counterexample for many problems in graph theory. The Petersen graph is named after Julius Petersen, who in 1898 constructed it to be the smallest bridgeless cubic graph with no three-edge-coloring.

<span class="mw-page-title-main">Snark (graph theory)</span> 3-regular graph with no 3-edge-coloring

In the mathematical field of graph theory, a snark is an undirected graph with exactly three edges per vertex whose edges cannot be colored with only three colors. In order to avoid trivial cases, snarks are often restricted to have additional requirements on their connectivity and on the length of their cycles. Infinitely many snarks exist.

In graph theory, the strong perfect graph theorem is a forbidden graph characterization of the perfect graphs as being exactly the graphs that have neither odd holes nor odd antiholes. It was conjectured by Claude Berge in 1961. A proof by Maria Chudnovsky, Neil Robertson, Paul Seymour, and Robin Thomas was announced in 2002 and published by them in 2006.

<span class="mw-page-title-main">Paul Seymour (mathematician)</span> British mathematician

Paul D. Seymour is a British mathematician known for his work in discrete mathematics, especially graph theory. He was responsible for important progress on regular matroids and totally unimodular matrices, the four colour theorem, linkless embeddings, graph minors and structure, the perfect graph conjecture, the Hadwiger conjecture, claw-free graphs, χ-boundedness, and the Erdős–Hajnal conjecture. Many of his recent papers are available from his website.

<span class="mw-page-title-main">Circulant graph</span> Undirected graph acted on by a vertex-transitive cyclic group of symmetries

In graph theory, a circulant graph is an undirected graph acted on by a cyclic group of symmetries which takes any vertex to any other vertex. It is sometimes called a cyclic graph, but this term has other meanings.

In graph theory, the Lovász conjecture (1969) is a classical problem on Hamiltonian paths in graphs. It says:

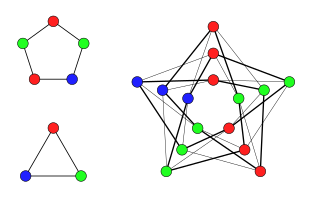
<span class="mw-page-title-main">Hedetniemi's conjecture</span> Conjecture in graph theory

In graph theory, Hedetniemi's conjecture, formulated by Stephen T. Hedetniemi in 1966, concerns the connection between graph coloring and the tensor product of graphs. This conjecture states that

<span class="mw-page-title-main">Hypohamiltonian graph</span> Type of graph in graph theory

In the mathematical field of graph theory, a graph G is said to be hypohamiltonian if G itself does not have a Hamiltonian cycle but every graph formed by removing a single vertex from G is Hamiltonian.

<span class="mw-page-title-main">Star (graph theory)</span> Tree graph with one central node and leaves of length 1

In graph theory, a starSk is the complete bipartite graph K1,k : a tree with one internal node and k leaves. Alternatively, some authors define Sk to be the tree of order k with maximum diameter 2; in which case a star of k > 2 has k − 1 leaves.

<span class="mw-page-title-main">Hamiltonian decomposition</span>

In graph theory, a branch of mathematics, a Hamiltonian decomposition of a given graph is a partition of the edges of the graph into Hamiltonian cycles. Hamiltonian decompositions have been studied both for undirected graphs and for directed graphs. In the undirected case a Hamiltonian decomposition can also be described as a 2-factorization of the graph such that each factor is connected.

In graph theory, a cycle decomposition is a decomposition into cycles. Every vertex in a graph that has a cycle decomposition must have even degree.

<span class="mw-page-title-main">Pancyclic graph</span>

In the mathematical study of graph theory, a pancyclic graph is a directed graph or undirected graph that contains cycles of all possible lengths from three up to the number of vertices in the graph. Pancyclic graphs are a generalization of Hamiltonian graphs, graphs which have a cycle of the maximum possible length.

Paul Allen Catlin was a mathematician, professor of mathematics who worked in graph theory and number theory. He wrote a significant paper on the series of chromatic numbers and Brooks' theorem, titled Hajós graph coloring conjecture: variations and counterexamples.

Haim Hanani was a Polish-born Israeli mathematician, known for his contributions to combinatorial design theory, in particular for the theory of pairwise balanced designs and for the proof of an existence theorem for Steiner quadruple systems. He is also known for the Hanani–Tutte theorem on odd crossings in non-planar graphs.

<span class="mw-page-title-main">Italo Jose Dejter</span>

Italo Jose Dejter is an Argentine-born American mathematician, a retired professor of mathematics and computer science from the University of Puerto Rico, and a researcher in algebraic topology, differential topology, graph theory, coding theory and combinatorial designs. He obtained a Licentiate degree in mathematics from University of Buenos Aires in 1967, arrived at Rutgers University in 1970 by means of a Guggenheim Fellowship and obtained a Ph.D. degree in mathematics in 1975 under the supervision of Professor Ted Petrie, with support of the National Science Foundation. He was a professor at the Federal University of Santa Catarina, Brazil, from 1977 to 1984, with grants from the National Council for Scientific and Technological Development, (CNPq).

Michael David Plummer is a retired mathematics professor from Vanderbilt University. His field of work is in graph theory in which he has produced over a hundred papers and publications. He has also spoken at over a hundred and fifty guest lectures around the world.

Alspach's conjecture is a mathematical theorem that characterizes the disjoint cycle covers of complete graphs with prescribed cycle lengths. It is named after Brian Alspach, who posed it as a research problem in 1981. A proof was published by Darryn Bryant, Daniel Horsley, and William Pettersson.

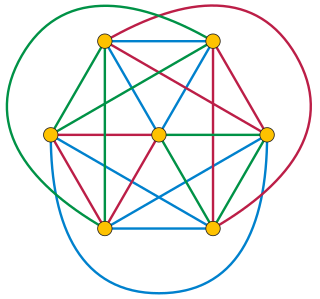
<span class="mw-page-title-main">Oberwolfach problem</span>

In mathematics, the Oberwolfach problem is an open problem that may be formulated either as a problem of scheduling seating assignments for diners, or more abstractly as a problem in graph theory, on the edge cycle covers of complete graphs. It is named after the Oberwolfach Research Institute for Mathematics, where the problem was posed in 1967 by Gerhard Ringel. It is known to be true for all sufficiently-large complete graphs.

In mathematics, a dicut is a partition of the vertices of a directed graph into two subsets, so that each edge that has an endpoint in both subsets is directed from the first subset to the second. Each strongly connected component of the graph must be entirely contained in one of the two subsets, so a strongly connected graph has no nontrivial dicuts.

References

  1. ↑ Brian Alspach at the Mathematics Genealogy Project
  2. 1 2 "Brian Alspach" (PDF). Mathematics with a Human Face: Mathematicians at Work. Math Central, University of Regina. Retrieved 2024-05-16.
  3. ↑ Morris, Joy; Šajna, Mateja (2005). "Brian Alspach and his work". Discrete Mathematics . 299 (1–3): 269–287. CiteSeerX   10.1.1.86.8422 . doi:10.1016/j.disc.2005.03.024.
  4. ↑ "Staff Profile". www.newcastle.edu.au. 2015-01-16. Retrieved 2019-09-12.
  5. ↑ Alspach, Brian (June 1967). "Cycles of Each Length in Regular Tournaments". Canadian Mathematical Bulletin . 10 (2): 283–286. doi: 10.4153/CMB-1967-028-6 .
  6. ↑ Alspach, Brian (1973). "Point-symmetric graphs and digraphs of prime order and transitive permutation groups of prime degree". Journal of Combinatorial Theory . Series B. 15 (1): 12–7. doi: 10.1016/0095-8956(73)90027-0 .
  7. ↑ Alspach, Brian; Parsons, T. D. (1979). "Isomorphism of circulant graphs and digraphs". Discrete Mathematics . 25 (2): 97–108. doi: 10.1016/0012-365X(79)90011-6 .
  8. ↑ Alspach, Brian; Parsons, T. D. (1982). "A construction for vertex–transitive graphs". Canadian Journal of Mathematics. 34 (2): 307–318. doi: 10.4153/cjm-1982-020-8 . S2CID   14128355.
  9. ↑ Alspach, B.; Zhang, Cun-Quan (1993), "Cycle covers of cubic multigraphs", Discrete Mathematics, 111 (1–3): 11–17, doi:10.1016/0012-365X(93)90135-G .
  10. ↑ Alspach, Brian; Gavlas, Heather (2001). "Cycle Decompositions of Kn and Kn−I". Journal of Combinatorial Theory . Series B. 81: 77–99. doi: 10.1006/jctb.2000.1996 .
  11. ↑ Bryant, Darryn; Horsley, Daniel; Pettersson, William (2014). "Cycle decompositions V: Complete graphs into cycles of arbitrary lengths". Proceedings of the London Mathematical Society. Third Series. 108 (5): 1153–1192. arXiv: 1204.3709 . doi:10.1112/plms/pdt051. MR   3214677. S2CID   40046099.
This page is based on this Wikipedia article
Text is available under the CC BY-SA 4.0 license; additional terms may apply.
Images, videos and audio are available under their respective licenses.