Formal definition
An irrational number is called a Brjuno number when the infinite sum
converges to a finite number.
Here:
- is the denominator of the nth convergent of the continued fraction expansion of .
- is a Brjuno function
In mathematics, a Brjuno number (sometimes spelled Bruno or Bryuno) is a special type of irrational number named for Russian mathematician Alexander Bruno, who introduced them in Brjuno (1971).
An irrational number is called a Brjuno number when the infinite sum
converges to a finite number.
Here:
Consider the golden ratio 𝜙:
Then the nth convergent can be found via the recurrence relation: [1]
It is easy to see that for , as a result
and since it can be proven that for any irrational number, 𝜙 is a Brjuno number. Moreover, a similar method can be used to prove that any irrational number whose continued fraction expansion ends with a string of 1's is a Brjuno number. [2]
By contrast, consider the constant with defined as
Then , so we have by the ratio test that diverges. is therefore not a Brjuno number. [3]
The Brjuno numbers are important in the one-dimensional analytic small divisors problems. Bruno improved the diophantine condition in Siegel's Theorem by showing that germs of holomorphic functions with linear part are linearizable if is a Brjuno number. Jean-ChristopheYoccoz ( 1995 ) showed in 1987 that Brjuno's condition is sharp; more precisely, he proved that for quadratic polynomials, this condition is not only sufficient but also necessary for linearizability.
Intuitively, these numbers do not have many large "jumps" in the sequence of convergents, in which the denominator of the (n + 1)th convergent is exponentially larger than that of the nth convergent. Thus, in contrast to the Liouville numbers, they do not have unusually accurate diophantine approximations by rational numbers.
The Brjuno sum or Brjuno function is
where:

The real Brjuno function is defined for irrational numbers [4]
and satisfies
for all irrational between 0 and 1.
Yoccoz's variant of the Brjuno sum defined as follows: [5]
where:
This sum converges if and only if the Brjuno sum does, and in fact their difference is bounded by a universal constant.

An algebraic number is a number that is a root of a non-zero polynomial in one variable with integer coefficients. For example, the golden ratio, , is an algebraic number, because it is a root of the polynomial x2 − x − 1. That is, it is a value for x for which the polynomial evaluates to zero. As another example, the complex number is algebraic because it is a root of x4 + 4.

The natural logarithm of a number is its logarithm to the base of the mathematical constant e, which is an irrational and transcendental number approximately equal to 2.718281828459. The natural logarithm of x is generally written as ln x, logex, or sometimes, if the base e is implicit, simply log x. Parentheses are sometimes added for clarity, giving ln(x), loge(x), or log(x). This is done particularly when the argument to the logarithm is not a single symbol, so as to prevent ambiguity.
A simple or regular continued fraction is a continued fraction with numerators all equal one, and denominators built from a sequence of integer numbers. The sequence can be finite or infinite, resulting in a finite continued fraction like
In number theory, a Liouville number is a real number with the property that, for every positive integer , there exists a pair of integers with such that
In mathematics, a power series is an infinite series of the form where an represents the coefficient of the nth term and c is a constant called the center of the series. Power series are useful in mathematical analysis, where they arise as Taylor series of infinitely differentiable functions. In fact, Borel's theorem implies that every power series is the Taylor series of some smooth function.

Euler's constant is a mathematical constant, usually denoted by the lowercase Greek letter gamma, defined as the limiting difference between the harmonic series and the natural logarithm, denoted here by log:

In mathematics, the n-th harmonic number is the sum of the reciprocals of the first n natural numbers:

The sum of the reciprocals of all prime numbers diverges; that is:
In mathematics, smooth functions and analytic functions are two very important types of functions. One can easily prove that any analytic function of a real argument is smooth. The converse is not true, as demonstrated with the counterexample below.
A continued fraction is a mathematical expression that can be written as a fraction with a denominator that is a sum that contains another simple or continued fraction. Depending on whether this iteration terminates with a simple fraction or not, the continued fraction is finite or infinite.

In mathematics, a Lambert series, named for Johann Heinrich Lambert, is a series taking the form
The Engel expansion of a positive real number x is the unique non-decreasing sequence of positive integers such that

Thomae's function is a real-valued function of a real variable that can be defined as:
In mathematics, convergence tests are methods of testing for the convergence, conditional convergence, absolute convergence, interval of convergence or divergence of an infinite series .
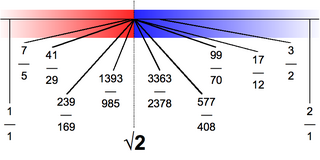
In mathematics, an irrationality measure of a real number is a measure of how "closely" it can be approximated by rationals.
In the mathematical theory of special functions, the Pochhammer k-symbol and the k-gamma function, introduced by Rafael Díaz and Eddy Pariguan are generalizations of the Pochhammer symbol and gamma function. They differ from the Pochhammer symbol and gamma function in that they can be related to a general arithmetic progression in the same manner as those are related to the sequence of consecutive integers.
The square root of 5 is the positive real number that, when multiplied by itself, gives the prime number 5. It is more precisely called the principal square root of 5, to distinguish it from the negative number with the same property. This number appears in the fractional expression for the golden ratio. It can be denoted in surd form as .
The Bailey–Borwein–Plouffe formula is a formula for π. It was discovered in 1995 by Simon Plouffe and is named after the authors of the article in which it was published, David H. Bailey, Peter Borwein, and Plouffe. Before that, it had been published by Plouffe on his own site. The formula is:
In number theory, specifically in Diophantine approximation theory, the Markov constant of an irrational number is the factor for which Dirichlet's approximation theorem can be improved for .