Related Research Articles

In geometry, a subset of a Euclidean space, or more generally an affine space over the reals, is convex if, given any two points in the subset, the subset contains the whole line segment that joins them. Equivalently, a convex set or a convex region is a subset that intersects every line into a single line segment . For example, a solid cube is a convex set, but anything that is hollow or has an indent, for example, a crescent shape, is not convex.

In geometry, the convex hull or convex envelope or convex closure of a shape is the smallest convex set that contains it. The convex hull may be defined either as the intersection of all convex sets containing a given subset of a Euclidean space, or equivalently as the set of all convex combinations of points in the subset. For a bounded subset of the plane, the convex hull may be visualized as the shape enclosed by a rubber band stretched around the subset.

Geometry of numbers is the part of number theory which uses geometry for the study of algebraic numbers. Typically, a ring of algebraic integers is viewed as a lattice in and the study of these lattices provides fundamental information on algebraic numbers. The geometry of numbers was initiated by Hermann Minkowski (1910).
In mathematics, the isoperimetric inequality is a geometric inequality involving the perimeter of a set and its volume. In -dimensional space the inequality lower bounds the surface area or perimeter of a set by its volume ,

In geometry, the Minkowski sum of two sets of position vectors A and B in Euclidean space is formed by adding each vector in A to each vector in B, i.e., the set
In mathematics, Hilbert's fourth problem in the 1900 Hilbert problems is a foundational question in geometry. In one statement derived from the original, it was to find — up to an isomorphism — all geometries that have an axiomatic system of the classical geometry, with those axioms of congruence that involve the concept of the angle dropped, and `triangle inequality', regarded as an axiom, added.
In mathematics, convex geometry is the branch of geometry studying convex sets, mainly in Euclidean space. Convex sets occur naturally in many areas: computational geometry, convex analysis, discrete geometry, functional analysis, geometry of numbers, integral geometry, linear programming, probability theory, game theory, etc.
In mathematics, the Brunn–Minkowski theorem is an inequality relating the volumes of compact subsets of Euclidean space. The original version of the Brunn–Minkowski theorem applied to convex sets; the generalization to compact nonconvex sets stated here is due to Lazar Lyusternik (1935).
In mathematics, a convex body in -dimensional Euclidean space is a compact convex set with non-empty interior.
In mathematics, a Borel measure μ on n-dimensional Euclidean space is called logarithmically concave if, for any compact subsets A and B of and 0 < λ < 1, one has
In mathematics, Anderson's theorem is a result in real analysis and geometry which says that the integral of an integrable, symmetric, unimodal, non-negative function f over an n-dimensional convex body K does not decrease if K is translated inwards towards the origin. This is a natural statement, since the graph of f can be thought of as a hill with a single peak over the origin; however, for n ≥ 2, the proof is not entirely obvious, as there may be points x of the body K where the value f(x) is larger than at the corresponding translate of x.
In mathematics, Shephard's problem, is the following geometrical question asked by Geoffrey Colin Shephard (1964): if K and L are centrally symmetric convex bodies in n-dimensional Euclidean space such that whenever K and L are projected onto a hyperplane, the volume of the projection of K is smaller than the volume of the projection of L, then does it follow that the volume of K is smaller than that of L?
In mathematics, Minkowski's first inequality for convex bodies is a geometrical result due to the German mathematician Hermann Minkowski. The inequality is closely related to the Brunn–Minkowski inequality and the isoperimetric inequality.
In mathematics, Vitale's random Brunn–Minkowski inequality is a theorem due to Richard Vitale that generalizes the classical Brunn–Minkowski inequality for compact subsets of n-dimensional Euclidean space Rn to random compact sets.
In mathematics, particularly, in asymptotic convex geometry, Milman's reverse Brunn–Minkowski inequality is a result due to Vitali Milman that provides a reverse inequality to the famous Brunn–Minkowski inequality for convex bodies in n-dimensional Euclidean space Rn. Namely, it bounds the volume of the Minkowski sum of two bodies from above in terms of the volumes of the bodies.
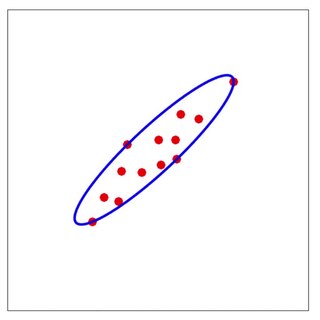
In mathematics, the John ellipsoid or Löwner-John ellipsoidE(K) associated to a convex body K in n-dimensional Euclidean space Rn can refer to the n-dimensional ellipsoid of maximal volume contained within K or the ellipsoid of minimal volume that contains K.
In mathematics, geometric measure theory (GMT) is the study of geometric properties of sets through measure theory. It allows mathematicians to extend tools from differential geometry to a much larger class of surfaces that are not necessarily smooth.
In differential geometry, the Minkowski problem, named after Hermann Minkowski, asks for the construction of a strictly convex compact surface S whose Gaussian curvature is specified. More precisely, the input to the problem is a strictly positive real function ƒ defined on a sphere, and the surface that is to be constructed should have Gaussian curvature ƒ(n ) at the point x, where n(x) denotes the normal to S at x. Eugenio Calabi stated: "From the geometric view point it [the Minkowski problem] is the Rosetta Stone, from which several related problems can be solved."
In convex geometry and the geometry of convex polytopes, the Blaschke sum of two polytopes is a polytope that has a facet parallel to each facet of the two given polytopes, with the same measure. When both polytopes have parallel facets, the measure of the corresponding facet in the Blaschke sum is the sum of the measures from the two given polytopes.
References
- Busemann, Herbert (1949). "A theorem on convex bodies of the Brunn-Minkowski type". Proc. Natl. Acad. Sci. U.S.A. 35 (1): 27–31. doi: 10.1073/pnas.35.1.27 . PMC 1062952 . PMID 16588849.
- Gardner, Richard J. (2002). "The Brunn-Minkowski inequality". Bull. Amer. Math. Soc. (N.S.). 39 (3): 355–405 (electronic). CiteSeerX 10.1.1.106.7344 . doi:10.1090/S0273-0979-02-00941-2.