
In geometry, a subset of a Euclidean space, or more generally an affine space over the reals, is convex if, given any two points in the subset, the subset contains the whole line segment that joins them. Equivalently, a convex set or a convex region is a subset that intersects every line into a single line segment . For example, a solid cube is a convex set, but anything that is hollow or has an indent, for example, a crescent shape, is not convex.

In mathematics and computational geometry, a Delaunay triangulation for a given set P of discrete points in a general position is a triangulation DT(P) such that no point in P is inside the circumcircle of any triangle in DT(P). Delaunay triangulations maximize the minimum of all the angles of the triangles in the triangulation; they tend to avoid sliver triangles. The triangulation is named after Boris Delaunay for his work on this topic from 1934.
In geometry, a polygon is a plane figure made up of line segments connected to form a closed polygonal chain.

In geometry a quadrilateral is a four-sided polygon, having four edges (sides) and four corners (vertices). The word is derived from the Latin words quadri, a variant of four, and latus, meaning "side". It is also called a tetragon, derived from greek "tetra" meaning "four" and "gon" meaning "corner" or "angle", in analogy to other polygons. Since "gon" means "angle", it is analogously called a quadrangle, or 4-angle. A quadrilateral with vertices , , and is sometimes denoted as .

In geometry, the convex hull or convex envelope or convex closure of a shape is the smallest convex set that contains it. The convex hull may be defined either as the intersection of all convex sets containing a given subset of a Euclidean space, or equivalently as the set of all convex combinations of points in the subset. For a bounded subset of the plane, the convex hull may be visualized as the shape enclosed by a rubber band stretched around the subset.
In mathematics, a subset of a given set is closed under an operation of the larger set if performing that operation on members of the subset always produces a member of that subset. For example, the natural numbers are closed under addition, but not under subtraction: 1 − 2 is not a natural number, although both 1 and 2 are.

Discrete geometry and combinatorial geometry are branches of geometry that study combinatorial properties and constructive methods of discrete geometric objects. Most questions in discrete geometry involve finite or discrete sets of basic geometric objects, such as points, lines, planes, circles, spheres, polygons, and so forth. The subject focuses on the combinatorial properties of these objects, such as how they intersect one another, or how they may be arranged to cover a larger object.
In finite geometry, the Fano plane is a finite projective plane with the smallest possible number of points and lines: 7 points and 7 lines, with 3 points on every line and 3 lines through every point. These points and lines cannot exist with this pattern of incidences in Euclidean geometry, but they can be given coordinates using the finite field with two elements. The standard notation for this plane, as a member of a family of projective spaces, is PG(2, 2). Here PG stands for "projective geometry", the first parameter is the geometric dimension and the second parameter is the order.

Graham's scan is a method of finding the convex hull of a finite set of points in the plane with time complexity O(n log n). It is named after Ronald Graham, who published the original algorithm in 1972. The algorithm finds all vertices of the convex hull ordered along its boundary. It uses a stack to detect and remove concavities in the boundary efficiently.

In mathematics, a cyclic order is a way to arrange a set of objects in a circle. Unlike most structures in order theory, a cyclic order is not modeled as a binary relation, such as "a < b". One does not say that east is "more clockwise" than west. Instead, a cyclic order is defined as a ternary relation [a, b, c], meaning "after a, one reaches b before c". For example, [June, October, February], but not [June, February, October], cf. picture. A ternary relation is called a cyclic order if it is cyclic, asymmetric, transitive, and connected. Dropping the "connected" requirement results in a partial cyclic order.

In mathematics, an extreme point of a convex set in a real or complex vector space is a point in which does not lie in any open line segment joining two points of In linear programming problems, an extreme point is also called vertex or corner point of

In geometry and combinatorics, an arrangement of hyperplanes is an arrangement of a finite set A of hyperplanes in a linear, affine, or projective space S. Questions about a hyperplane arrangement A generally concern geometrical, topological, or other properties of the complement, M(A), which is the set that remains when the hyperplanes are removed from the whole space. One may ask how these properties are related to the arrangement and its intersection semilattice. The intersection semilattice of A, written L(A), is the set of all subspaces that are obtained by intersecting some of the hyperplanes; among these subspaces are S itself, all the individual hyperplanes, all intersections of pairs of hyperplanes, etc. (excluding, in the affine case, the empty set). These intersection subspaces of A are also called the flats ofA. The intersection semilattice L(A) is partially ordered by reverse inclusion.
In mathematics, a norm is a function from a real or complex vector space to the non-negative real numbers that behaves in certain ways like the distance from the origin: it commutes with scaling, obeys a form of the triangle inequality, and is zero only at the origin. In particular, the Euclidean distance in a Euclidean space is defined by a norm on the associated Euclidean vector space, called the Euclidean norm, the 2-norm, or, sometimes, the magnitude of the vector. This norm can be defined as the square root of the inner product of a vector with itself.

In mathematics, the real coordinate space of dimension n, denoted Rn or , is the set of the n-tuples of real numbers, that is the set of all sequences of n real numbers. Special cases are called the real lineR1 and the real coordinate planeR2. With component-wise addition and scalar multiplication, it is a real vector space, and its elements are called coordinate vectors.
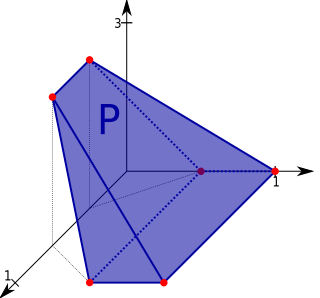
A convex polytope is a special case of a polytope, having the additional property that it is also a convex set contained in the -dimensional Euclidean space . Most texts use the term "polytope" for a bounded convex polytope, and the word "polyhedron" for the more general, possibly unbounded object. Others allow polytopes to be unbounded. The terms "bounded/unbounded convex polytope" will be used below whenever the boundedness is critical to the discussed issue. Yet other texts identify a convex polytope with its boundary.
In mathematics, a triangle group is a group that can be realized geometrically by sequences of reflections across the sides of a triangle. The triangle can be an ordinary Euclidean triangle, a triangle on the sphere, or a hyperbolic triangle. Each triangle group is the symmetry group of a tiling of the Euclidean plane, the sphere, or the hyperbolic plane by congruent triangles called Möbius triangles, each one a fundamental domain for the action.
In geometry, collinearity of a set of points is the property of their lying on a single line. A set of points with this property is said to be collinear. In greater generality, the term has been used for aligned objects, that is, things being "in a line" or "in a row".
In linear algebra and matroid theory, Rota's basis conjecture is an unproven conjecture concerning rearrangements of bases, named after Gian-Carlo Rota. It states that, if X is either a vector space of dimension n or more generally a matroid of rank n, with n disjoint bases Bi, then it is possible to arrange the elements of these bases into an n × n matrix in such a way that the rows of the matrix are exactly the given bases and the columns of the matrix are also bases. That is, it should be possible to find a second set of n disjoint bases Ci, each of which consists of one element from each of the bases Bi.
In mathematics, symmetric cones, sometimes called domains of positivity, are open convex self-dual cones in Euclidean space which have a transitive group of symmetries, i.e. invertible operators that take the cone onto itself. By the Koecher–Vinberg theorem these correspond to the cone of squares in finite-dimensional real Euclidean Jordan algebras, originally studied and classified by Jordan, von Neumann & Wigner (1934). The tube domain associated with a symmetric cone is a noncompact Hermitian symmetric space of tube type. All the algebraic and geometric structures associated with the symmetric space can be expressed naturally in terms of the Jordan algebra. The other irreducible Hermitian symmetric spaces of noncompact type correspond to Siegel domains of the second kind. These can be described in terms of more complicated structures called Jordan triple systems, which generalize Jordan algebras without identity.
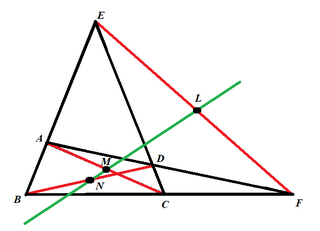
In geometry, the Newton–Gauss line is the line joining the midpoints of the three diagonals of a complete quadrilateral.














