Convex hull algorithms

Algorithms that construct convex hulls of various objects have a broad range of applications in mathematics and computer science.

In computational geometry, numerous algorithms are proposed for computing the convex hull of a finite set of points, with various computational complexities.

Computing the convex hull means that a non-ambiguous and efficient representation of the required convex shape is constructed. The complexity of the corresponding algorithms is usually estimated in terms of n, the number of input points, and sometimes also in terms of h, the number of points on the convex hull.

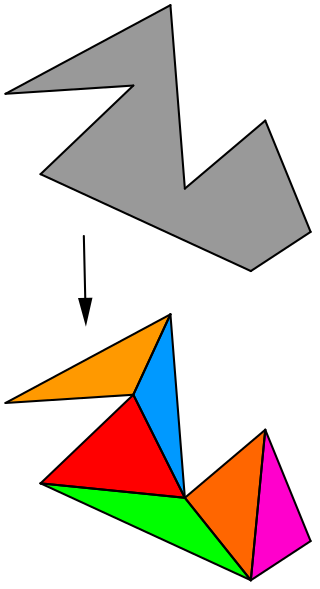
Planar case

Consider the general case when the input to the algorithm is a finite unordered set of points on a Cartesian plane. An important special case, in which the points are given in the order of traversal of a simple polygon's boundary, is described later in a separate subsection.

If not all points are on the same line, then their convex hull is a convex polygon whose vertices are some of the points in the input set. Its most common representation is the list of its vertices ordered along its boundary clockwise or counterclockwise. In some applications it is convenient to represent a convex polygon as an intersection of a set of half-planes.

Lower bound on computational complexity

For a finite set of points in the plane, the lower bound on the computational complexity of finding the convex hull represented as a convex polygon is easily shown to be the same as for sorting using the following reduction. For the set ${\displaystyle x_{1},\dots ,x_{n}}$ numbers to sort consider the set ${\displaystyle (x_{1},x_{1}^{2}),\dots ,(x_{n},x_{n}^{2})}$ of points in the plane. Since they lie on a parabola, which is a convex curve, it is easy to see that the vertices of the convex hull, when traversed along the boundary, produce the sorted order of the numbers ${\displaystyle x_{1},\dots ,x_{n}}$. Clearly, linear time is required for the described transformation of numbers into points and then extracting their sorted order. Therefore, in the general case the convex hull of n points cannot be computed more quickly than sorting.

The standard Ω(n log n) lower bound for sorting is proven in the decision tree model of computing, in which only numerical comparisons but not arithmetic operations can be performed; however, in this model, convex hulls cannot be computed at all. Sorting also requires Ω(n log n) time in the algebraic decision tree model of computation, a model that is more suitable for convex hulls, and in this model convex hulls also require Ω(n log n) time. ^[1] However, in models of computer arithmetic that allow numbers to be sorted more quickly than O(n log n) time, for instance by using integer sorting algorithms, planar convex hulls can also be computed more quickly: the Graham scan algorithm for convex hulls consists of a single sorting step followed by a linear amount of additional work.

Optimal output-sensitive algorithms

As stated above, the complexity of finding a convex hull as a function of the input size n is lower bounded by Ω(n log n). However, the complexity of some convex hull algorithms can be characterized in terms of both input size n and the output size h (the number of points in the hull). Such algorithms are called output-sensitive algorithms. They may be asymptotically more efficient than Θ(n log n) algorithms in cases when h = o(n).

The lower bound on worst-case running time of output-sensitive convex hull algorithms was established to be Ω(n log h) in the planar case. ^[1] There are several algorithms which attain this optimal time complexity. The earliest one was introduced by Kirkpatrick and Seidel in 1986 (who called it "the ultimate convex hull algorithm"). A much simpler algorithm was developed by Chan in 1996, and is called Chan's algorithm.

Algorithms

Known convex hull algorithms are listed below, ordered by the date of first publication. Time complexity of each algorithm is stated in terms of the number of inputs points n and the number of points on the hull h. Note that in the worst case h may be as large as n.

• Gift wrapping , a.k.a. Jarvis march — O(nh)
  One of the simplest (although not the most time efficient in the worst case) planar algorithms. Created independently by Chand & Kapur in 1970 and R. A. Jarvis in 1973. It has O(nh) time complexity, where n is the number of points in the set, and h is the number of points in the hull. In the worst case the complexity is O(n²).
• Graham scan — O(n log n)
  A slightly more sophisticated, but much more efficient algorithm, published by Ronald Graham in 1972. If the points are already sorted by one of the coordinates or by the angle to a fixed vector, then the algorithm takes O(n) time.
• Quickhull
  Created independently in 1977 by W. Eddy and in 1978 by A. Bykat. Just like the quicksort algorithm, it has the expected time complexity of O(n log n), but may degenerate to O(n²) in the worst case.
• Divide and conquer — O(n log n)
  Another O(n log n) algorithm, published in 1977 by Preparata and Hong. This algorithm is also applicable to the three dimensional case.
• Monotone chain , a.k.a. Andrew's algorithm— O(n log n)
  Published in 1979 by A. M. Andrew. The algorithm can be seen as a variant of Graham scan which sorts the points lexicographically by their coordinates. When the input is already sorted, the algorithm takes O(n) time.
• Incremental convex hull algorithm — O(n log n)
  Published in 1984 by Michael Kallay.
• Kirkpatrick–Seidel algorithm — O(n log h)
  The first optimal output-sensitive algorithm. It modifies the divide and conquer algorithm by using the technique of marriage-before-conquest and low-dimensional linear programming. Published by Kirkpatrick and Seidel in 1986.
• Chan's algorithm — O(n log h)
  A simpler optimal output-sensitive algorithm created by Chan in 1996. It combines gift wrapping with the execution of an O(n log n) algorithm (such as Graham scan) on small subsets of the input.

Akl–Toussaint heuristic

The following simple heuristic is often used as the first step in implementations of convex hull algorithms to improve their performance. It is based on the efficient convex hull algorithm by Selim Akl and G. T. Toussaint, 1978. The idea is to quickly exclude many points that would not be part of the convex hull anyway. This method is based on the following idea. Find the two points with the lowest and highest x-coordinates, and the two points with the lowest and highest y-coordinates. (Each of these operations takes O(n).) These four points form a convex quadrilateral, and all points that lie in this quadrilateral (except for the four initially chosen vertices) are not part of the convex hull. Finding all of these points that lie in this quadrilateral is also O(n), and thus, the entire operation is O(n). Optionally, the points with smallest and largest sums of x- and y-coordinates as well as those with smallest and largest differences of x- and y-coordinates can also be added to the quadrilateral, thus forming an irregular convex octagon, whose insides can be safely discarded. If the points are random variables, then for a narrow but commonly encountered class of probability density functions, this throw-away pre-processing step will make a convex hull algorithm run in linear expected time, even if the worst-case complexity of the convex hull algorithm is quadratic in n. ^[2]

On-line and dynamic convex hull problems

The discussion above considers the case when all input points are known in advance. One may consider two other settings. ^[1]

• Online convex hull problem: Input points are obtained sequentially one by one. After each point arrives on input, the convex hull for the pointset obtained so far must be efficiently computed.
• Dynamic convex hull maintenance: The input points may be sequentially inserted or deleted, and the convex hull must be updated after each insert/delete operation.

Insertion of a point may increase the number of vertices of a convex hull at most by 1, while deletion may convert an n-vertex convex hull into an n-1-vertex one.

The online version may be handled with O(log n) per point, which is asymptotically optimal. The dynamic version may be handled with O(log²n) per operation. ^[1]

Simple polygon

Main article: Convex hull of a simple polygon

The convex hull of a simple polygon is divided by the polygon into pieces, one of which is the polygon itself and the rest are pockets bounded by a piece of the polygon boundary and a single hull edge. Although many algorithms have been published for the problem of constructing the convex hull of a simple polygon, nearly half of them are incorrect. ^[3] McCallum and Avis provided the first correct algorithm. ^[4] A later simplification by Graham & Yao (1983) and Lee (1983) uses only a single stack data structure. Their algorithm traverses the polygon clockwise, starting from its leftmost vertex. As it does, it stores a convex sequence of vertices on the stack, the ones that have not yet been identified as being within pockets. At each step, the algorithm follows a path along the polygon from the stack top to the next vertex that is not in one of the two pockets adjacent to the stack top. Then, while the top two vertices on the stack together with this new vertex are not in convex position, it pops the stack, before finally pushing the new vertex onto the stack. When the clockwise traversal reaches the starting point, the algorithm returns the sequence of stack vertices as the hull. ^{[5] [6]}

Higher dimensions

A number of algorithms are known for the three-dimensional case, as well as for arbitrary dimensions. ^[7] Chan's algorithm is used for dimensions 2 and 3, and Quickhull is used for computation of the convex hull in higher dimensions. ^[8]

For a finite set of points, the convex hull is a convex polyhedron in three dimensions, or in general a convex polytope for any number of dimensions, whose vertices are some of the points in the input set. Its representation is not so simple as in the planar case, however. In higher dimensions, even if the vertices of a convex polytope are known, construction of its faces is a non-trivial task, as is the dual problem of constructing the vertices given the faces. The size of the output face information may be exponentially larger than the size of the input vertices, and even in cases where the input and output are both of comparable size the known algorithms for high-dimensional convex hulls are not output-sensitive due both to issues with degenerate inputs and with intermediate results of high complexity. ^[9]

See also

• Orthogonal convex hull

References

1. Preparata, Shamos, Computational Geometry, Chapter "Convex Hulls: Basic Algorithms"
2. Luc Devroye and Godfried Toussaint, "A note on linear expected time algorithms for finding convex hulls," Computing, Vol. 26, 1981, pp. 361-366.
3. Aloupis, Greg. "A History of Linear-time Convex Hull Algorithms for Simple Polygons" . Retrieved October 11, 2020.
4. McCallum, Duncan; Avis, David (1979), "A linear algorithm for finding the convex hull of a simple polygon", Information Processing Letters , 9 (5): 201–206, doi:10.1016/0020-0190(79)90069-3, MR   0552534
5. Graham, Ronald L.; Yao, F. Frances (1983), "Finding the convex hull of a simple polygon", Journal of Algorithms , 4 (4): 324–331, doi:10.1016/0196-6774(83)90013-5, MR   0729228
6. Lee, D. T. (1983), "On finding the convex hull of a simple polygon", International Journal of Computer and Information Sciences, 12 (2): 87–98, doi:10.1007/BF00993195, MR   0724699, S2CID   28600832
7. See David Mount's Lecture Notes, including Lecture 4 for recent developments, including Chan's algorithm.
8. Barber, C. Bradford; Dobkin, David P.; Huhdanpaa, Hannu (1 December 1996). "The quickhull algorithm for convex hulls" (PDF). ACM Transactions on Mathematical Software. 22 (4): 469–483. doi: 10.1145/235815.235821 .
9. Avis, David; Bremner, David; Seidel, Raimund (1997), "How good are convex hull algorithms?", Computational Geometry: Theory and Applications , 7 (5–6): 265–301, doi: 10.1016/S0925-7721(96)00023-5 .

Further reading

• Thomas H. Cormen, Charles E. Leiserson, Ronald L. Rivest, and Clifford Stein. Introduction to Algorithms , Second Edition. MIT Press and McGraw-Hill, 2001. ISBN   0-262-03293-7. Section 33.3: Finding the convex hull, pp. 947–957.
• Franco P. Preparata, S.J. Hong. Convex Hulls of Finite Sets of Points in Two and Three Dimensions, Commun. ACM, vol. 20, no. 2, pp. 87–93, 1977.
• Mark de Berg; Marc van Kreveld; Mark Overmars & Otfried Schwarzkopf (2000). Computational Geometry (2nd revised ed.). Springer-Verlag. ISBN   978-3-540-65620-3. Section 1.1: An Example: Convex Hulls (describes classical algorithms for 2-dimensional convex hulls). Chapter 11: Convex Hulls: pp. 235–250 (describes a randomized algorithm for 3-dimensional convex hulls due to Clarkson and Shor).

External links

• Weisstein, Eric W. "Convex Hull". MathWorld .
• 2D, 3D, and dD Convex Hull in CGAL, the Computational Geometry Algorithms Library
• Qhull code for Convex Hull, Delaunay Triangulation, Voronoi Diagram, and Halfspace Intersection
• Demo as Flash swf, Jarvis, Graham, Quick (divide and conquer) and Chan algorithms
• Gift wrapping algorithm in C#