An ideal gas is a theoretical gas composed of many randomly moving point particles that are not subject to interparticle interactions. The ideal gas concept is useful because it obeys the ideal gas law, a simplified equation of state, and is amenable to analysis under statistical mechanics. The requirement of zero interaction can often be relaxed if, for example, the interaction is perfectly elastic or regarded as point-like collisions.

Surface tension is the tendency of liquid surfaces at rest to shrink into the minimum surface area possible. Surface tension is what allows objects with a higher density than water such as razor blades and insects to float on a water surface without becoming even partly submerged.

Foams are materials formed by trapping pockets of gas in a liquid or solid.

In surface science, surface energy quantifies the disruption of intermolecular bonds that occurs when a surface is created. In solid-state physics, surfaces must be intrinsically less energetically favorable than the bulk of the material, otherwise there would be a driving force for surfaces to be created, removing the bulk of the material by sublimation. The surface energy may therefore be defined as the excess energy at the surface of a material compared to the bulk, or it is the work required to build an area of a particular surface. Another way to view the surface energy is to relate it to the work required to cut a bulk sample, creating two surfaces. There is "excess energy" as a result of the now-incomplete, unrealized bonding between the two created surfaces.
In mathematics, the discrete Laplace operator is an analog of the continuous Laplace operator, defined so that it has meaning on a graph or a discrete grid. For the case of a finite-dimensional graph, the discrete Laplace operator is more commonly called the Laplacian matrix.

Wetting is the ability of a liquid to displace gas to maintain contact with a solid surface, resulting from intermolecular interactions when the two are brought together. This happens in presence of a gaseous phase or another liquid phase not miscible with the first one. The degree of wetting (wettability) is determined by a force balance between adhesive and cohesive forces. There are two types of wetting: non-reactive wetting and reactive wetting.
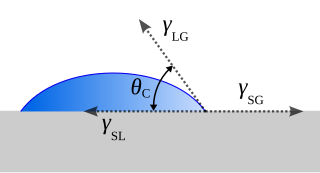
The contact angle is the angle between a liquid surface and a solid surface where they meet. More specifically, it is the angle between the surface tangent on the liquid–vapor interface and the tangent on the solid–liquid interface at their intersection. It quantifies the wettability of a solid surface by a liquid via the Young equation.

A dendrite in metallurgy is a characteristic tree-like structure of crystals growing as molten metal solidifies, the shape produced by faster growth along energetically favourable crystallographic directions. This dendritic growth has large consequences in regard to material properties.
In fluid statics, capillary pressure is the pressure between two immiscible fluids in a thin tube, resulting from the interactions of forces between the fluids and solid walls of the tube. Capillary pressure can serve as both an opposing or driving force for fluid transport and is a significant property for research and industrial purposes. It is also observed in natural phenomena.
In fluid dynamics the Eötvös number (Eo), also called the Bond number (Bo), is a dimensionless number measuring the importance of gravitational forces compared to surface tension forces for the movement of liquid front. Alongside the Capillary number, commonly denoted , which represents the contribution of viscous drag, is useful for studying the movement of fluid in porous or granular media, such as soil. The Bond number is also used to characterize the shape of bubbles or drops moving in a surrounding fluid. The two names used for this dimensionless term commemorate the Hungarian physicist Loránd Eötvös (1848–1919) and the English physicist Wilfrid Noel Bond (1897–1937), respectively. The term Eötvös number is more frequently used in Europe, while Bond number is commonly used in other parts of the world.
The Kelvin equation describes the change in vapour pressure due to a curved liquid–vapor interface, such as the surface of a droplet. The vapor pressure at a convex curved surface is higher than that at a flat surface. The Kelvin equation is dependent upon thermodynamic principles and does not allude to special properties of materials. It is also used for determination of pore size distribution of a porous medium using adsorption porosimetry. The equation is named in honor of William Thomson, also known as Lord Kelvin.
In physics, the Green's function for the Laplacian in three variables is used to describe the response of a particular type of physical system to a point source. In particular, this Green's function arises in systems that can be described by Poisson's equation, a partial differential equation (PDE) of the form where is the Laplace operator in , is the source term of the system, and is the solution to the equation. Because is a linear differential operator, the solution to a general system of this type can be written as an integral over a distribution of source given by : where the Green's function for Laplacian in three variables describes the response of the system at the point to a point source located at : and the point source is given by , the Dirac delta function.
In physics, the Young–Laplace equation is an algebraic equation that describes the capillary pressure difference sustained across the interface between two static fluids, such as water and air, due to the phenomenon of surface tension or wall tension, although use of the latter is only applicable if assuming that the wall is very thin. The Young–Laplace equation relates the pressure difference to the shape of the surface or wall and it is fundamentally important in the study of static capillary surfaces. It is a statement of normal stress balance for static fluids meeting at an interface, where the interface is treated as a surface : where is the Laplace pressure, the pressure difference across the fluid interface, is the surface tension, is the unit normal pointing out of the surface, is the mean curvature, and and are the principal radii of curvature. Note that only normal stress is considered, because a static interface is possible only in the absence of tangential stress.

The capillary length or capillary constant is a length scaling factor that relates gravity and surface tension. It is a fundamental physical property that governs the behavior of menisci, and is found when body forces (gravity) and surface forces are in equilibrium.
In fluid mechanics and mathematics, a capillary surface is a surface that represents the interface between two different fluids. As a consequence of being a surface, a capillary surface has no thickness in slight contrast with most real fluid interfaces.

In materials science and biology, capillary condensation is the "process by which multilayer adsorption from the vapor [phase] into a porous medium proceeds to the point at which pore spaces become filled with condensed liquid from the vapor [phase]." The unique aspect of capillary condensation is that vapor condensation occurs below the saturation vapor pressure, Psat, of the pure liquid. This result is due to an increased number of van der Waals interactions between vapor phase molecules inside the confined space of a capillary. Once condensation has occurred, a meniscus immediately forms at the liquid-vapor interface which allows for equilibrium below the saturation vapor pressure. Meniscus formation is dependent on the surface tension of the liquid and the shape of the capillary, as shown by the Young-Laplace equation. As with any liquid-vapor interface involving a meniscus, the Kelvin equation provides a relation for the difference between the equilibrium vapor pressure and the saturation vapor pressure. A capillary does not necessarily have to be a tubular, closed shape, but can be any confined space with respect to its surroundings.
The spinning drop method or rotating drop method is one of the methods used to measure interfacial tension. Measurements are carried out in a rotating horizontal tube which contains a dense fluid. A drop of a less dense liquid or a gas bubble is placed inside the fluid. Since the rotation of the horizontal tube creates a centrifugal force towards the tube walls, the liquid drop will start to deform into an elongated shape; this elongation stops when the interfacial tension and centrifugal forces are balanced. The surface tension between the two liquids can then be derived from the shape of the drop at this equilibrium point. A device used for such measurements is called a “spinning drop tensiometer”.
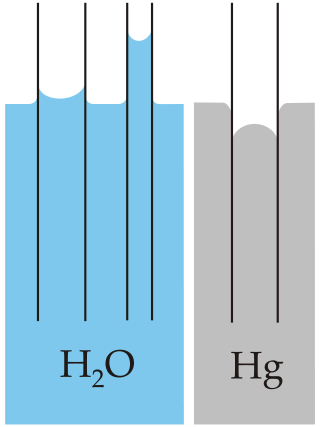
Jurin's law, or capillary rise, is the simplest analysis of capillary action—the induced motion of liquids in small channels—and states that the maximum height of a liquid in a capillary tube is inversely proportional to the tube's diameter. Capillary action is one of the most common fluid mechanical effects explored in the field of microfluidics. Jurin's law is named after James Jurin, who discovered it between 1718 and 1719. His quantitative law suggests that the maximum height of liquid in a capillary tube is inversely proportional to the tube's diameter. The difference in height between the surroundings of the tube and the inside, as well as the shape of the meniscus, are caused by capillary action. The mathematical expression of this law can be derived directly from hydrostatic principles and the Young–Laplace equation. Jurin's law allows the measurement of the surface tension of a liquid and can be used to derive the capillary length.
The Gibbs–Thomson effect, in common physics usage, refers to variations in vapor pressure or chemical potential across a curved surface or interface. The existence of a positive interfacial energy will increase the energy required to form small particles with high curvature, and these particles will exhibit an increased vapor pressure. See Ostwald–Freundlich equation. More specifically, the Gibbs–Thomson effect refers to the observation that small crystals are in equilibrium with their liquid melt at a lower temperature than large crystals. In cases of confined geometry, such as liquids contained within porous media, this leads to a depression in the freezing point / melting point that is inversely proportional to the pore size, as given by the Gibbs–Thomson equation.
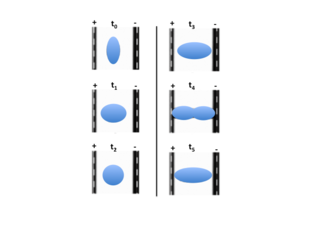
Electrohydrodynamic droplet deformation is a phenomenon that occurs when liquid droplets suspended in a second immiscible liquid are exposed to an oscillating electric field. Under these conditions, the droplet will periodically deform between prolate and oblate ellipsoidal shapes. The characteristic frequency and magnitude of the deformation is determined by a balance of electrodynamic, hydrodynamic, and capillary stresses acting on the droplet interface. This phenomenon has been studied extensively both mathematically and experimentally because of the complex fluid dynamics that occur. Characterization and modulation of electrodynamic droplet deformation is of particular interest for engineering applications because of the growing need to improve the performance of complex industrial processes(e.g. two-phase cooling, crude oil demulsification). The primary advantage of using oscillatory droplet deformation to improve these engineering processes is that the phenomenon does not require sophisticated machinery or the introduction of heat sources. This effectively means that improving performance via oscillatory droplet deformation is simple and in no way diminishes the effectiveness of the existing engineering system.