In integral calculus, an elliptic integral is one of a number of related functions defined as the value of certain integrals. Originally, they arose in connection with the problem of finding the arc length of an ellipse and were first studied by Giulio Fagnano and Leonhard Euler. Modern mathematics defines an "elliptic integral" as any function f which can be expressed in the form

A sphere is a geometrical object in three-dimensional space that is the surface of a ball.
In electrodynamics, elliptical polarization is the polarization of electromagnetic radiation such that the tip of the electric field vector describes an ellipse in any fixed plane intersecting, and normal to, the direction of propagation. An elliptically polarized wave may be resolved into two linearly polarized waves in phase quadrature, with their polarization planes at right angles to each other. Since the electric field can rotate clockwise or counterclockwise as it propagates, elliptically polarized waves exhibit chirality.

In mathematics, curvature is any of several strongly related concepts in geometry. Intuitively, the curvature is the amount by which a curve deviates from being a straight line, or a surface deviates from being a plane.
In the mathematical field of complex analysis elliptic functions are a special kind of meromorphic functions, that satisfy two periodicity conditions. They are named elliptic functions because they come from elliptic integrals. Originally those integrals occurred at the calculation of the arc length of an ellipse.
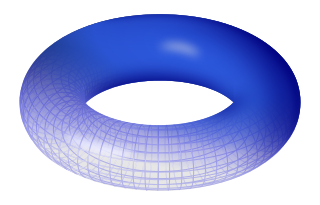
In geometry, a torus is a surface of revolution generated by revolving a circle in three-dimensional space about an axis that is coplanar with the circle.

An ellipsoid is a surface that may be obtained from a sphere by deforming it by means of directional scalings, or more generally, of an affine transformation.

In geometry, a paraboloid is a quadric surface that has exactly one axis of symmetry and no center of symmetry. The term "paraboloid" is derived from parabola, which refers to a conic section that has a similar property of symmetry.
In differential geometry, the Ricci curvature tensor, named after Gregorio Ricci-Curbastro, is a geometric object which is determined by a choice of Riemannian or pseudo-Riemannian metric on a manifold. It can be considered, broadly, as a measure of the degree to which the geometry of a given metric tensor differs locally from that of ordinary Euclidean space or pseudo-Euclidean space.

In differential geometry, the Gaussian curvature or Gauss curvatureΚ of a surface at a point is the product of the principal curvatures, κ1 and κ2, at the given point:
In mathematics, the Jacobi elliptic functions are a set of basic elliptic functions, and auxiliary theta functions, that are of historical importance. They are found in the description of the motion of a pendulum, as well as in the design of electronic elliptic filters. While trigonometric functions are defined with reference to a circle, the Jacobi elliptic functions are a generalization which refer to other conic sections, the ellipse in particular. The relation to trigonometric functions is contained in the notation, for example, by the matching notation sn for sin. The Jacobi elliptic functions are used more often in practical problems than the Weierstrass elliptic functions as they do not require notions of complex analysis to be defined and/or understood. They were introduced by Carl Gustav Jakob Jacobi (1829).
In mathematics, the mean curvature of a surface is an extrinsic measure of curvature that comes from differential geometry and that locally describes the curvature of an embedded surface in some ambient space such as Euclidean space.
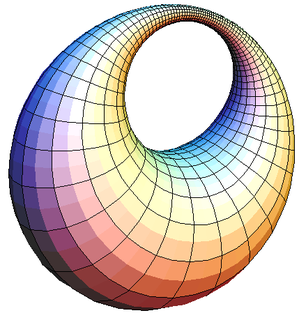
In mathematics, a Dupin cyclide or cyclide of Dupin is any geometric inversion of a standard torus, cylinder or double cone. In particular, these latter are themselves examples of Dupin cyclides. They were discovered by Charles Dupin in his 1803 dissertation under Gaspard Monge. The key property of a Dupin cyclide is that it is a channel surface in two different ways. This property means that Dupin cyclides are natural objects in Lie sphere geometry.
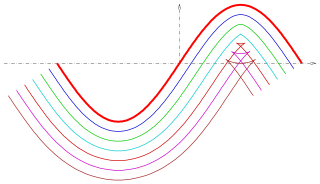
A parallel of a curve is the
A parametric surface is a surface in the Euclidean space which is defined by a parametric equation with two parameters :\mathbb {R} ^{2}\to \mathbb {R} ^{3}} . Parametric representation is a very general way to specify a surface, as well as implicit representation. Surfaces that occur in two of the main theorems of vector calculus, Stokes' theorem and the divergence theorem, are frequently given in a parametric form. The curvature and arc length of curves on the surface, surface area, differential geometric invariants such as the first and second fundamental forms, Gaussian, mean, and principal curvatures can all be computed from a given parametrization.
In Riemannian geometry and pseudo-Riemannian geometry, the Gauss–Codazzi equations are fundamental formulas which link together the induced metric and second fundamental form of a submanifold of a Riemannian or pseudo-Riemannian manifold.

In mathematics, the differential geometry of surfaces deals with the differential geometry of smooth surfaces with various additional structures, most often, a Riemannian metric. Surfaces have been extensively studied from various perspectives: extrinsically, relating to their embedding in Euclidean space and intrinsically, reflecting their properties determined solely by the distance within the surface as measured along curves on the surface. One of the fundamental concepts investigated is the Gaussian curvature, first studied in depth by Carl Friedrich Gauss, who showed that curvature was an intrinsic property of a surface, independent of its isometric embedding in Euclidean space.
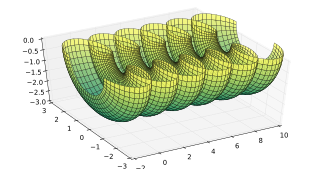
In differential geometry, constant-mean-curvature (CMC) surfaces are surfaces with constant mean curvature. This includes minimal surfaces as a subset, but typically they are treated as special case.

In physics and geometry, the nodary is the curve that is traced by the focus of a hyperbola as it rolls without slipping along the axis, a roulette curve.

In geometry, two conic sections are called confocal, if they have the same foci. Because ellipses and hyperbolas possess two foci, there are confocal ellipses, confocal hyperbolas and confocal mixtures of ellipses and hyperbolas. In the mixture of confocal ellipses and hyperbolas, any ellipse intersects any hyperbola orthogonally. Parabolas possess only one focus, so, by convention, confocal parabolas have the same focus and the same axis of symmetry. Consequently, any point not on the axis of symmetry lies on two confocal parabolas which intersect orthogonally.



















