| Part of a series on | |||||||
| Arithmetic logic circuits | |||||||
|---|---|---|---|---|---|---|---|
| Quick navigation | |||||||
Components
| |||||||
See also | |||||||
 | This article needs additional citations for verification .(December 2009) |
In electronics, a carry-select adder is a particular way to implement an adder, which is a logic element that computes the -bit sum of two -bit numbers. The carry-select adder is simple but rather fast, having a gate level depth of .
The carry-select adder generally consists of ripple-carry adders and a multiplexer. Adding two n-bit numbers with a carry-select adder is done with two adders (therefore two ripple-carry adders), in order to perform the calculation twice, one time with the assumption of the carry-in being zero and the other assuming it will be one. After the two results are calculated, the correct sum, as well as the correct carry-out, is then selected with the multiplexer once the correct carry-in is known.
The number of bits in each carry select block can be uniform, or variable. The optimal delay occurs when variable size of the blocks is applied [1] . When variable, the block size should have a delay, from addition inputs A and B to the carry out, equal to that of the multiplexer chain leading into it, so that the carry out is calculated just in time. The delay is derived from uniform sizing, where the ideal number of full-adder elements per block is equal to the square root of the number of bits being added, since that will yield an equal number of MUX delays.
Above is the basic building block of a carry-select adder, where the block size is 4. Two 4-bit ripple-carry adders are multiplexed together, where the resulting carry and sum bits are selected by the carry-in. Since one ripple-carry adder assumes a carry-in of 0, and the other assumes a carry-in of 1, selecting which adder had the correct assumption via the actual carry-in yields the desired result.
A 16-bit carry-select adder with a uniform block size of 4 can be created with three of these blocks and a 4-bit ripple-carry adder. Since carry-in is known at the beginning of computation, a carry select block is not needed for the first four bits. The delay of this adder will be four full adder delays, plus three MUX delays.
A 16-bit carry-select adder with variable size can be similarly created. Here we show an adder with block sizes of 2-2-3-4-5, this is the special type of Variable-sized carry select adder, called as square root carry select adder [2] . This break-up is ideal when the full-adder delay is equal to the MUX delay, which is unlikely. The total delay is two full adder delays, and four mux delays. We try to make the delay through the two carry chains and the delay of the previous stage carry equal.
A conditional sum adder [3] is a recursive structure based on the carry-select adder. In the conditional sum adder, the MUX level chooses between two n/2-bit inputs that are themselves built as conditional-sum adder. The bottom level of the tree consists of pairs of 2-bit adders (1 half adder and 3 full adders) plus 2 single-bit multiplexers.
The conditional sum adder suffers from a very large fan-out of the intermediate carry outputs. The fan out can be as high as n/2 on the last level, where drives all multiplexers from to .
The carry-select adder design can be complemented with a carry-lookahead adder structure to generate the MUX inputs, thus gaining even greater performance as a parallel prefix adder while potentially reducing area.
An example is shown in the Kogge–Stone adder article.
In computer science and information theory, a Huffman code is a particular type of optimal prefix code that is commonly used for lossless data compression. The process of finding or using such a code is Huffman coding, an algorithm developed by David A. Huffman while he was a Sc.D. student at MIT, and published in the 1952 paper "A Method for the Construction of Minimum-Redundancy Codes".
In statistics, the standard deviation is a measure of the amount of variation of the values of a variable about its mean. A low standard deviation indicates that the values tend to be close to the mean of the set, while a high standard deviation indicates that the values are spread out over a wider range. The standard deviation is commonly used in the determination of what constitutes an outlier and what does not.
In electronics, a multiplexer, also known as a data selector, is a device that selects between several analog or digital input signals and forwards the selected input to a single output line. The selection is directed by a separate set of digital inputs known as select lines. A multiplexer of inputs has select lines, which are used to select which input line to send to the output.
Two's complement is the most common method of representing signed integers on computers, and more generally, fixed point binary values. Two's complement uses the binary digit with the greatest value as the sign to indicate whether the binary number is positive or negative; when the most significant bit is 1 the number is signed as negative and when the most significant bit is 0 the number is signed as positive. As a result, non-negative numbers are represented as themselves: 6 is 0110, zero is 0000, and -6 is 1010. Note that while the number of binary bits is fixed throughout a computation it is otherwise arbitrary.
A barrel shifter is a digital circuit that can shift a data word by a specified number of bits without the use of any sequential logic, only pure combinational logic, i.e. it inherently provides a binary operation. It can however in theory also be used to implement unary operations, such as logical shift left, in cases where limited by a fixed amount. One way to implement a barrel shifter is as a sequence of multiplexers where the output of one multiplexer is connected to the input of the next multiplexer in a way that depends on the shift distance. A barrel shifter is often used to shift and rotate n-bits in modern microprocessors, typically within a single clock cycle.
In numerical analysis, the Kahan summation algorithm, also known as compensated summation, significantly reduces the numerical error in the total obtained by adding a sequence of finite-precision floating-point numbers, compared to the obvious approach. This is done by keeping a separate running compensation, in effect extending the precision of the sum by the precision of the compensation variable.
In CPU design, the use of a sum-addressed decoder (SAD) or sum-addressed memory (SAM) decoder is a method of reducing the latency of the CPU cache access and address calculation. This is achieved by fusing the address generation sum operation with the decode operation in the cache SRAM.
In the history of computer hardware, some early reduced instruction set computer central processing units used a very similar architectural solution, now called a classic RISC pipeline. Those CPUs were: MIPS, SPARC, Motorola 88000, and later the notional CPU DLX invented for education.
An adder, or summer, is a digital circuit that performs addition of numbers. In many computers and other kinds of processors, adders are used in the arithmetic logic units (ALUs). They are also used in other parts of the processor, where they are used to calculate addresses, table indices, increment and decrement operators and similar operations.
In Boolean algebra, any Boolean function can be expressed in the canonical disjunctive normal form (CDNF), minterm canonical form, or Sum of Products as a disjunction (OR) of minterms. The De Morgan dual is the canonical conjunctive normal form (CCNF), maxterm canonical form, or Product of Sums which is a conjunction (AND) of maxterms. These forms can be useful for the simplification of Boolean functions, which is of great importance in the optimization of Boolean formulas in general and digital circuits in particular.
A carry-lookahead adder (CLA) or fast adder is a type of electronics adder used in digital logic. A carry-lookahead adder improves speed by reducing the amount of time required to determine carry bits. It can be contrasted with the simpler, but usually slower, ripple-carry adder (RCA), for which the carry bit is calculated alongside the sum bit, and each stage must wait until the previous carry bit has been calculated to begin calculating its own sum bit and carry bit. The carry-lookahead adder calculates one or more carry bits before the sum, which reduces the wait time to calculate the result of the larger-value bits of the adder.
A carry-skip adder is an adder implementation that improves on the delay of a ripple-carry adder with little effort compared to other adders. The improvement of the worst-case delay is achieved by using several carry-skip adders to form a block-carry-skip adder.
Early completion is a property of some classes of asynchronous circuit. It means that the output of a circuit may be available as soon as sufficient inputs have arrived to allow it to be determined. For example, if all of the inputs to a mux have arrived, and all are the same, but the select line has not yet arrived, the circuit can still produce an output. Since all the inputs are identical, the select line is irrelevant.
XOR gate is a digital logic gate that gives a true output when the number of true inputs is odd. An XOR gate implements an exclusive or from mathematical logic; that is, a true output results if one, and only one, of the inputs to the gate is true. If both inputs are false (0/LOW) or both are true, a false output results. XOR represents the inequality function, i.e., the output is true if the inputs are not alike otherwise the output is false. A way to remember XOR is "must have one or the other but not both".
A Wallace multiplier is a hardware implementation of a binary multiplier, a digital circuit that multiplies two integers. It uses a selection of full and half adders to sum partial products in stages until two numbers are left. Wallace multipliers reduce as much as possible on each layer, whereas Dadda multipliers try to minimize the required number of gates by postponing the reduction to the upper layers.
The Dadda multiplier is a hardware binary multiplier design invented by computer scientist Luigi Dadda in 1965. It uses a selection of full and half adders to sum the partial products in stages until two numbers are left. The design is similar to the Wallace multiplier, but the different reduction tree reduces the required number of gates and makes it slightly faster.
A carry-save adder is a type of digital adder, used to efficiently compute the sum of three or more binary numbers. It differs from other digital adders in that it outputs two numbers, and the answer of the original summation can be achieved by adding these outputs together. A carry save adder is typically used in a binary multiplier, since a binary multiplier involves addition of more than two binary numbers after multiplication. A big adder implemented using this technique will usually be much faster than conventional addition of those numbers.
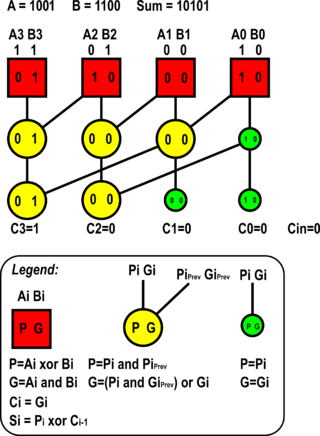
In computing, the Kogge–Stone adder is a parallel prefix form of carry-lookahead adder. Other parallel prefix adders (PPA) include the Sklansky adder (SA), Brent–Kung adder (BKA), the Han–Carlson adder (HCA), the fastest known variation, the Lynch–Swartzlander spanning tree adder (STA), Knowles adder (KNA) and Beaumont-Smith adder (BSA).
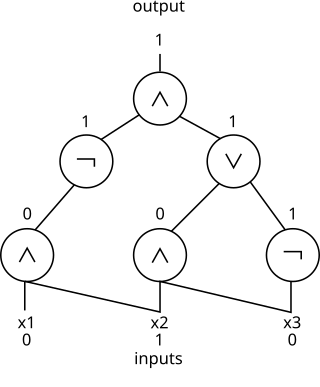
In computational complexity theory and circuit complexity, a Boolean circuit is a mathematical model for combinational digital logic circuits. A formal language can be decided by a family of Boolean circuits, one circuit for each possible input length.
A truth table is a mathematical table used in logic—specifically in connection with Boolean algebra, Boolean functions, and propositional calculus—which sets out the functional values of logical expressions on each of their functional arguments, that is, for each combination of values taken by their logical variables. In particular, truth tables can be used to show whether a propositional expression is true for all legitimate input values, that is, logically valid.
