
In physics, spacetime, also called the space-time continuum, is a mathematical model that fuses the three dimensions of space and the one dimension of time into a single four-dimensional continuum. Spacetime diagrams are useful in visualizing and understanding relativistic effects, such as how different observers perceive where and when events occur.
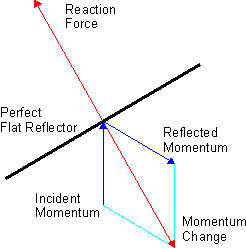
Radiation pressure is mechanical pressure exerted upon a surface due to the exchange of momentum between the object and the electromagnetic field. This includes the momentum of light or electromagnetic radiation of any wavelength that is absorbed, reflected, or otherwise emitted by matter on any scale. The associated force is called the radiation pressure force, or sometimes just the force of light.
Causality is the relationship between causes and effects. While causality is also a topic studied from the perspectives of philosophy and physics, it is operationalized so that causes of an event must be in the past light cone of the event and ultimately reducible to fundamental interactions. Similarly, a cause cannot have an effect outside its future light cone.
The world line of an object is the path that an object traces in 4-dimensional spacetime. It is an important concept of modern physics, and particularly theoretical physics.

The observable universe is a spherical region of the universe consisting of all matter that can be observed from Earth or its space-based telescopes and exploratory probes at the present time; the electromagnetic radiation from these objects has had time to reach the Solar System and Earth since the beginning of the cosmological expansion. Assuming the universe is isotropic, the distance to the edge of the observable universe is roughly the same in every direction. That is, the observable universe is a spherical region centered on the observer. Every location in the universe has its own observable universe, which may or may not overlap with the one centered on Earth.
In mathematical physics, a closed timelike curve (CTC) is a world line in a Lorentzian manifold, of a material particle in spacetime, that is "closed", returning to its starting point. This possibility was first discovered by Willem Jacob van Stockum in 1937 and later confirmed by Kurt Gödel in 1949, who discovered a solution to the equations of general relativity (GR) allowing CTCs known as the Gödel metric; and since then other GR solutions containing CTCs have been found, such as the Tipler cylinder and traversable wormholes. If CTCs exist, their existence would seem to imply at least the theoretical possibility of time travel backwards in time, raising the spectre of the grandfather paradox, although the Novikov self-consistency principle seems to show that such paradoxes could be avoided. Some physicists speculate that the CTCs which appear in certain GR solutions might be ruled out by a future theory of quantum gravity which would replace GR, an idea which Stephen Hawking labeled the chronology protection conjecture. Others note that if every closed timelike curve in a given spacetime passes through an event horizon, a property which can be called chronological censorship, then that spacetime with event horizons excised would still be causally well behaved and an observer might not be able to detect the causal violation.
The Penrose–Hawking singularity theorems are a set of results in general relativity that attempt to answer the question of when gravitation produces singularities. The Penrose singularity theorem is a theorem in semi-Riemannian geometry and its general relativistic interpretation predicts a gravitational singularity in black hole formation. The Hawking singularity theorem is based on the Penrose theorem and it is interpreted as a gravitational singularity in the Big Bang situation. Penrose was awarded the Nobel Prize in Physics in 2020 "for the discovery that black hole formation is a robust prediction of the general theory of relativity", which he shared with Reinhard Genzel and Andrea Ghez.

In special and general relativity, a light cone is the path that a flash of light, emanating from a single event and traveling in all directions, would take through spacetime.
In physics, the principle of locality states that an object is influenced directly only by its immediate surroundings. A theory that includes the principle of locality is said to be a "local theory". This is an alternative to the concept of instantaneous, or "non-local" action at a distance. Locality evolved out of the field theories of classical physics. The idea is that for a cause at one point to have an effect at another point, something in the space between those points must mediate the action. To exert an influence, something, such as a wave or particle, must travel through the space between the two points, carrying the influence.

In theoretical physics, a Penrose diagram is a two-dimensional diagram capturing the causal relations between different points in spacetime through a conformal treatment of infinity. It is an extension of the Minkowski diagram of special relativity where the vertical dimension represents time, and the horizontal dimension represents a space dimension. Using this design, all light rays take a 45° path . Locally, the metric on a Penrose diagram is conformally equivalent to the metric of the spacetime depicted. The conformal factor is chosen such that the entire infinite spacetime is transformed into a Penrose diagram of finite size, with infinity on the boundary of the diagram. For spherically symmetric spacetimes, every point in the Penrose diagram corresponds to a 2-dimensional sphere .
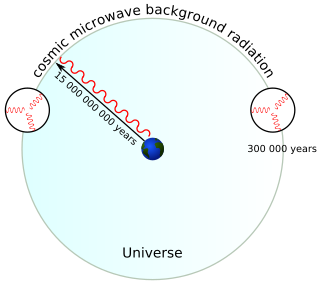
The horizon problem is a cosmological fine-tuning problem within the Big Bang model of the universe. It arises due to the difficulty in explaining the observed homogeneity of causally disconnected regions of space in the absence of a mechanism that sets the same initial conditions everywhere. It was first pointed out by Wolfgang Rindler in 1956.
The Gödel metric, also known as the Gödel solution or Gödel universe, is an exact solution, found in 1949 by Kurt Gödel, of the Einstein field equations in which the stress–energy tensor contains two terms: the first representing the matter density of a homogeneous distribution of swirling dust particles, and the second associated with a negative cosmological constant.
A cosmological horizon is a measure of the distance from which one could possibly retrieve information. This observable constraint is due to various properties of general relativity, the expanding universe, and the physics of Big Bang cosmology. Cosmological horizons set the size and scale of the observable universe. This article explains a number of these horizons.

The expansion of the universe is the increase in distance between gravitationally unbound parts of the observable universe with time. It is an intrinsic expansion, so it does not mean that the universe expands "into" anything or that space exists "outside" it. To any observer in the universe, it appears that all but the nearest galaxies recede at speeds that are proportional to their distance from the observer, on average. While objects cannot move faster than light, this limitation applies only with respect to local reference frames and does not limit the recession rates of cosmologically distant objects.
In general relativity, an absolute horizon is a boundary in spacetime, defined with respect to the external universe, inside which events cannot affect an external observer. Light emitted inside the horizon can never reach the observer, and anything that passes through the horizon from the observer's side is never seen again by the observer. An absolute horizon is thought of as the boundary of a black hole.

A spacetime diagram is a graphical illustration of locations in space at various times, especially in the special theory of relativity. Spacetime diagrams can show the geometry underlying phenomena like time dilation and length contraction without mathematical equations.
In mathematical physics, the causal structure of a Lorentzian manifold describes the causal relationships between points in the manifold.

In relativity, an event is anything that happens that has a specific time and place in spacetime. For example, a glass breaking on the floor is an event; it occurs at a unique place and a unique time. Strictly speaking, the notion of an event is an idealization, in the sense that it specifies a definite time and place, whereas any actual event is bound to have a finite extent, both in time and in space.
In astrophysics, an event horizon is a boundary beyond which events cannot affect an observer. Wolfgang Rindler coined the term in the 1950s.
The measure problem in cosmology concerns how to compute the ratios of universes of different types within a multiverse. It typically arises in the context of eternal inflation. The problem arises because different approaches to calculating these ratios yield different results, and it is not clear which approach is correct.












