In differential geometry, Cayley's ruled cubic surface is the ruled cubic surface
In projective coordinates it is .
It contains a (double) line of self-intersection and two pinch points. [1]
In differential geometry, Cayley's ruled cubic surface is the ruled cubic surface
In projective coordinates it is .
It contains a (double) line of self-intersection and two pinch points. [1]
In mathematics, the discriminant of a polynomial is a quantity that depends on the coefficients and allows deducing some properties of the roots without computing them. More precisely, it is a polynomial function of the coefficients of the original polynomial. The discriminant is widely used in polynomial factoring, number theory, and algebraic geometry.

In mathematics, the graph of a function is the set of ordered pairs , where In the common case where and are real numbers, these pairs are Cartesian coordinates of points in a plane and often form a curve. The graphical representation of the graph of a function is also known as a plot.

In geometry, a hyperboloid of revolution, sometimes called a circular hyperboloid, is the surface generated by rotating a hyperbola around one of its principal axes. A hyperboloid is the surface obtained from a hyperboloid of revolution by deforming it by means of directional scalings, or more generally, of an affine transformation.

In geometry, a normal is an object that is perpendicular to a given object. For example, the normal line to a plane curve at a given point is the line perpendicular to the tangent line to the curve at the point.
In mathematics, the Cayley–Dickson construction, sometimes also known as the Cayley–Dickson process or the Cayley–Dickson procedure produces a sequence of algebras over the field of real numbers, each with twice the dimension of the previous one. It is named after Arthur Cayley and Leonard Eugene Dickson. The algebras produced by this process are known as Cayley–Dickson algebras, for example complex numbers, quaternions, and octonions. These examples are useful composition algebras frequently applied in mathematical physics.

In mathematics, F4 is a Lie group and also its Lie algebra f4. It is one of the five exceptional simple Lie groups. F4 has rank 4 and dimension 52. The compact form is simply connected and its outer automorphism group is the trivial group. Its fundamental representation is 26-dimensional.

In mathematics, a Cayley graph, also known as a Cayley color graph, Cayley diagram, group diagram, or color group, is a graph that encodes the abstract structure of a group. Its definition is suggested by Cayley's theorem, and uses a specified set of generators for the group. It is a central tool in combinatorial and geometric group theory. The structure and symmetry of Cayley graphs makes them particularly good candidates for constructing expander graphs.

In mathematics, a cubic surface is a surface in 3-dimensional space defined by one polynomial equation of degree 3. Cubic surfaces are fundamental examples in algebraic geometry. The theory is simplified by working in projective space rather than affine space, and so cubic surfaces are generally considered in projective 3-space . The theory also becomes more uniform by focusing on surfaces over the complex numbers rather than the real numbers; note that a complex surface has real dimension 4. A simple example is the Fermat cubic surface

In mathematics, a cubic plane curve is a plane algebraic curve C defined by a cubic equation

A cone is a three-dimensional geometric shape that tapers smoothly from a flat base to a point called the apex or vertex that is not contained in the base.
In mathematics, the Cayley transform, named after Arthur Cayley, is any of a cluster of related things. As originally described by Cayley (1846), the Cayley transform is a mapping between skew-symmetric matrices and special orthogonal matrices. The transform is a homography used in real analysis, complex analysis, and quaternionic analysis. In the theory of Hilbert spaces, the Cayley transform is a mapping between linear operators.
In abstract algebra, the split-quaternions or coquaternions form an algebraic structure introduced by James Cockle in 1849 under the latter name. They form an associative algebra of dimension four over the real numbers.

In geometry, the Whitney umbrella or Whitney's umbrella, named after American mathematician Hassler Whitney, and sometimes called a Cayley umbrella, is a specific self-intersecting ruled surface placed in three dimensions. It is the union of all straight lines that pass through points of a fixed parabola and are perpendicular to a fixed straight line which is parallel to the axis of the parabola and lies on its perpendicular bisecting plane.
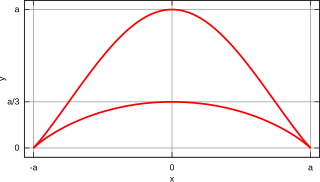
In geometry, the bicorn, also known as a cocked hat curve due to its resemblance to a bicorne, is a rational quartic curve defined by the equation It has two cusps and is symmetric about the y-axis.

In group theory, more precisely in geometric group theory, a hyperbolic group, also known as a word hyperbolic group or Gromov hyperbolic group, is a finitely generated group equipped with a word metric satisfying certain properties abstracted from classical hyperbolic geometry. The notion of a hyperbolic group was introduced and developed by Mikhail Gromov. The inspiration came from various existing mathematical theories: hyperbolic geometry but also low-dimensional topology, and combinatorial group theory. In a very influential chapter from 1987, Gromov proposed a wide-ranging research program. Ideas and foundational material in the theory of hyperbolic groups also stem from the work of George Mostow, William Thurston, James W. Cannon, Eliyahu Rips, and many others.

In algebraic geometry, the Cayley surface, named after Arthur Cayley, is a cubic nodal surface in 3-dimensional projective space with four conical points. It can be given by the equation
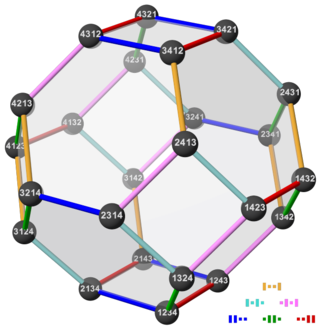
In mathematics, the permutohedron (also spelled permutahedron) of order n is an (n − 1)-dimensional polytope embedded in an n-dimensional space. Its vertex coordinates (labels) are the permutations of the first n natural numbers. The edges identify the shortest possible paths (sets of transpositions) that connect two vertices (permutations). Two permutations connected by an edge differ in only two places (one transposition), and the numbers on these places are neighbors (differ in value by 1).

In mathematics, a Cayley–Klein metric is a metric on the complement of a fixed quadric in a projective space which is defined using a cross-ratio. The construction originated with Arthur Cayley's essay "On the theory of distance" where he calls the quadric the absolute. The construction was developed in further detail by Felix Klein in papers in 1871 and 1873, and subsequent books and papers. The Cayley–Klein metrics are a unifying idea in geometry since the method is used to provide metrics in hyperbolic geometry, elliptic geometry, and Euclidean geometry. The field of non-Euclidean geometry rests largely on the footing provided by Cayley–Klein metrics.

In mathematics, Fresnel's wave surface, found by Augustin-Jean Fresnel in 1822, is a quartic surface describing the propagation of light in an optically biaxial crystal. Wave surfaces are special cases of tetrahedroids which are in turn special cases of Kummer surfaces.

In mathematics, the Dixon elliptic functions sm and cm are two elliptic functions that map from each regular hexagon in a hexagonal tiling to the whole complex plane. Because these functions satisfy the identity , as real functions they parametrize the cubic Fermat curve , just as the trigonometric functions sine and cosine parametrize the unit circle .