In fluid mechanics, the Cheerios effect is a colloquial name for the phenomenon of floating objects appearing to either attract or repel one another. The example which gives the effect its name is the observation that pieces of breakfast cereal (for example, Cheerios) floating on the surface of a bowl will tend to clump together, or appear to stick to the side of the bowl. [1]
The effect is observed in small objects which are supported by the surface of a liquid. There are two types of such objects: objects which are sufficiently buoyant that they will always float on the surface (for example, Cheerios in milk), and objects which are heavy enough to sink when immersed, but not so heavy as to overcome the surface tension of the liquid (for example, steel pins on water). Objects of the same type will appear to attract one another, and objects of opposite types will appear to repel one another.
In addition, the same attractive or repulsive effect can be observed between objects and the wall of the container. Once again there are two possibilities: the interface between the liquid and the container wall is either a concave or a convex meniscus. Buoyant objects will be attracted in the case of a concave meniscus and repelled for convex. Non-buoyant floating objects will do the opposite.
All objects in a fluid experience two opposed forces in the vertical direction: gravity (determined by the mass of the object) and buoyancy (determined by the density of the fluid and the volume of liquid displaced by the object). If the buoyant force is greater than the force of gravity acting on an object, it will rise to the top of the liquid. On the other hand, an object immersed in a liquid which experiences a gravitational force greater than its buoyant force will sink.
At the surface of the liquid, a third effect comes into play - surface tension. This effect is due to the fact that molecules of the liquid are more strongly attracted to each other than they are to the air above the liquid. As such, non-wetting objects on the surface of the liquid will experience an upward force due to surface tension. If the upward force is sufficient to balance the force of gravity on the object, it will float on the surface of the liquid, while deforming the surface down. By contrast, objects with a net positive buoyancy will deform the water surface upward around them as they press against the surface.
This deformation of the liquid surface, combined with the net upwards or downwards force experienced by each object, is the cause of the Cheerios effect. Objects experiencing a net upward force will follow the surface of the liquid as it curves upward. Therefore two objects with an upward deformation will move toward each other as each follows the surface of the liquid upward. Similarly, objects with a net downward force will follow the curve of the liquid surface in the downward direction, and will move horizontally together as they do so. [2]
The same principle holds at the side of the container, where the surface of the liquid is deformed by the meniscus effect. If the container is wetting with respect to the liquid, the meniscus will slope upwards at the wall of the container, and buoyant objects will move towards the wall as a result of travelling upward along the surface. By contrast, non-buoyant floating objects will move away from the walls of such a container for the same reason.
More complex behavior resulting from the same principles can be observed in shapes which do not have simple concave or convex meniscus behavior. When such objects come close to each other they rotate in the plane of the water surface until they find an optimum relative orientation then move toward each other. [3] [4]
Writing in the American Journal of Physics, Dominic Vella and L. Mahadevan of Harvard University discuss the Cheerios effect and suggest that it may be useful in the study of the self-assembly of small structures. [5] They calculate the force between two spheres of density and radius floating distance apart in liquid of density as
where is the surface tension, is a modified Bessel function of the first kind, is the Bond number, and
is a nondimensional factor in terms of the contact angle . Here is a convenient meniscus length scale.
A centripetal force is a force that makes a body follow a curved path. The direction of the centripetal force is always orthogonal to the motion of the body and towards the fixed point of the instantaneous center of curvature of the path. Isaac Newton described it as "a force by which bodies are drawn or impelled, or in any way tend, towards a point as to a centre". In Newtonian mechanics, gravity provides the centripetal force causing astronomical orbits.
Surface tension is the tendency of liquid surfaces at rest to shrink into the minimum surface area possible. Surface tension is what allows objects with a higher density than water such as razor blades and insects to float on a water surface without becoming even partly submerged.
Buoyancy, or upthrust, is a gravitational force, a net upward force exerted by a fluid that opposes the weight of a partially or fully immersed object. In a column of fluid, pressure increases with depth as a result of the weight of the overlying fluid. Thus, the pressure at the bottom of a column of fluid is greater than at the top of the column. Similarly, the pressure at the bottom of an object submerged in a fluid is greater than at the top of the object. The pressure difference results in a net upward force on the object. The magnitude of the force is proportional to the pressure difference, and is equivalent to the weight of the fluid that would otherwise occupy the submerged volume of the object, i.e. the displaced fluid.
Archimedes' principle states that the upward buoyant force that is exerted on a body immersed in a fluid, whether fully or partially, is equal to the weight of the fluid that the body displaces. Archimedes' principle is a law of physics fundamental to fluid mechanics. It was formulated by Archimedes of Syracuse.
In fluid dynamics, the pressure coefficient is a dimensionless number which describes the relative pressures throughout a flow field. The pressure coefficient is used in aerodynamics and hydrodynamics. Every point in a fluid flow field has its own unique pressure coefficient, Cp.
Internal waves are gravity waves that oscillate within a fluid medium, rather than on its surface. To exist, the fluid must be stratified: the density must change with depth/height due to changes, for example, in temperature and/or salinity. If the density changes over a small vertical distance, the waves propagate horizontally like surface waves, but do so at slower speeds as determined by the density difference of the fluid below and above the interface. If the density changes continuously, the waves can propagate vertically as well as horizontally through the fluid.
Wetting is the ability of a liquid to displace gas to maintain contact with a solid surface, resulting from intermolecular interactions when the two are brought together. This happens in presence of a gaseous phase or another liquid phase not miscible with the first one. The degree of wetting (wettability) is determined by a force balance between adhesive and cohesive forces. There are two types of wetting: non-reactive wetting and reactive wetting.
The Marangoni effect is the mass transfer along an interface between two phases due to a gradient of the surface tension. In the case of temperature dependence, this phenomenon may be called thermo-capillary convection.
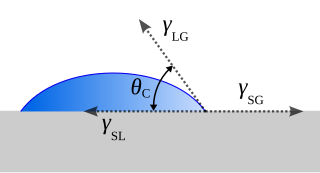
The contact angle is the angle between a liquid surface and a solid surface where they meet. More specifically, it is the angle between the surface tangent on the liquid–vapor interface and the tangent on the solid–liquid interface at their intersection. It quantifies the wettability of a solid surface by a liquid via the Young equation.
In fluid statics, capillary pressure is the pressure between two immiscible fluids in a thin tube, resulting from the interactions of forces between the fluids and solid walls of the tube. Capillary pressure can serve as both an opposing or driving force for fluid transport and is a significant property for research and industrial purposes. It is also observed in natural phenomena.
In physics, the Young–Laplace equation is an algebraic equation that describes the capillary pressure difference sustained across the interface between two static fluids, such as water and air, due to the phenomenon of surface tension or wall tension, although use of the latter is only applicable if assuming that the wall is very thin. The Young–Laplace equation relates the pressure difference to the shape of the surface or wall and it is fundamentally important in the study of static capillary surfaces. It is a statement of normal stress balance for static fluids meeting at an interface, where the interface is treated as a surface : where is the Laplace pressure, the pressure difference across the fluid interface, is the surface tension, is the unit normal pointing out of the surface, is the mean curvature, and and are the principal radii of curvature. Note that only normal stress is considered, because a static interface is possible only in the absence of tangential stress.
The capillary length or capillary constant is a length scaling factor that relates gravity and surface tension. It is a fundamental physical property that governs the behavior of menisci, and is found when body forces (gravity) and surface forces are in equilibrium.
In fluid mechanics and mathematics, a capillary surface is a surface that represents the interface between two different fluids. As a consequence of being a surface, a capillary surface has no thickness in slight contrast with most real fluid interfaces.
In fluid dynamics, the Oseen equations describe the flow of a viscous and incompressible fluid at small Reynolds numbers, as formulated by Carl Wilhelm Oseen in 1910. Oseen flow is an improved description of these flows, as compared to Stokes flow, with the (partial) inclusion of convective acceleration.
Nuclear magnetic resonance (NMR) in porous materials covers the application of using NMR as a tool to study the structure of porous media and various processes occurring in them. This technique allows the determination of characteristics such as the porosity and pore size distribution, the permeability, the water saturation, the wettability, etc.
In surface chemistry, disjoining pressure according to an IUPAC definition arises from an attractive interaction between two surfaces. For two flat and parallel surfaces, the value of the disjoining pressure can be calculated as the derivative of the Gibbs energy of interaction per unit area in respect to distance. There is also a related concept of disjoining force, which can be viewed as disjoining pressure times the surface area of the interacting surfaces.
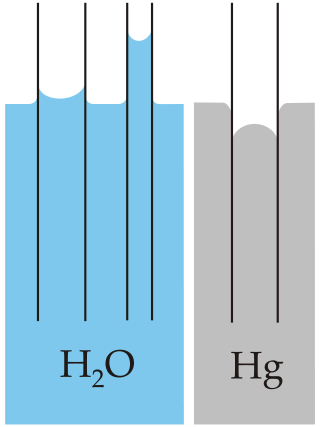
Jurin's law, or capillary rise, is the simplest analysis of capillary action—the induced motion of liquids in small channels—and states that the maximum height of a liquid in a capillary tube is inversely proportional to the tube's diameter. Capillary action is one of the most common fluid mechanical effects explored in the field of microfluidics. Jurin's law is named after James Jurin, who discovered it between 1718 and 1719. His quantitative law suggests that the maximum height of liquid in a capillary tube is inversely proportional to the tube's diameter. The difference in height between the surroundings of the tube and the inside, as well as the shape of the meniscus, are caused by capillary action. The mathematical expression of this law can be derived directly from hydrostatic principles and the Young–Laplace equation. Jurin's law allows the measurement of the surface tension of a liquid and can be used to derive the capillary length.
Elasto-capillarity is the ability of capillary force to deform an elastic material. From the viewpoint of mechanics, elastocapillarity phenomena essentially involve competition between the elastic strain energy in the bulk and the energy on the surfaces/interfaces. In the modeling of these phenomena, some challenging issues are, among others, the exact characterization of energies at the micro scale, the solution of strongly nonlinear problems of structures with large deformation and moving boundary conditions, and instability of either solid structures or droplets/films.The capillary forces are generally negligible in the analysis of macroscopic structures but often play a significant role in many phenomena at small scales.
Flotation of flexible objects is a phenomenon in which the bending of a flexible material allows an object to displace a greater amount of fluid than if it were completely rigid. This ability to displace more fluid translates directly into an ability to support greater loads, giving the flexible structure an advantage over a similarly rigid one. Inspiration to study the effects of elasticity are taken from nature, where plants, such as black pepper, and animals living at the water surface have evolved to take advantage of the load-bearing benefits elasticity imparts.
In the theory of capillarity, Bosanquet equation is an improved modification of the simpler Lucas–Washburn theory for the motion of a liquid in a thin capillary tube or a porous material that can be approximated as a large collection of capillaries. In the Lucas–Washburn model, the inertia of the fluid is ignored, leading to the assumption that flow is continuous under constant viscous laminar Poiseuille flow conditions without considering the effects of mass transport undergoing acceleration occurring at the start of flow and at points of changing internal capillary geometry. The Bosanquet equation is a differential equation that is second-order in the time derivative, similar to Newton's Second Law, and therefore takes into account the fluid inertia. Equations of motion, like the Washburn's equation, that attempt to explain a velocity as proportional to a driving force are often described with the term Aristotelian mechanics.
