Choice function

Last updated February 18, 2024

A choice function (selector, selection) is a mathematical function f that is defined on some collection X of nonempty sets and assigns some element of each set S in that collection to S by f(S); f(S) maps S to some element of S. In other words, f is a choice function for X if and only if it belongs to the direct product of X.

An example

Let X = { {1,4,7}, {9}, {2,7} }. Then the function f defined by f({1, 4, 7}) = 7, f({9}) = 9 and f({2, 7}) = 2 is a choice function on X.

History and importance

Ernst Zermelo (1904) introduced choice functions as well as the axiom of choice (AC) and proved the well-ordering theorem,^[1] which states that every set can be well-ordered. AC states that every set of nonempty sets has a choice function. A weaker form of AC, the axiom of countable choice (AC_ω) states that every countable set of nonempty sets has a choice function. However, in the absence of either AC or AC_ω, some sets can still be shown to have a choice function.

If $X$ is a finite set of nonempty sets, then one can construct a choice function for $X$ by picking one element from each member of $X.$ This requires only finitely many choices, so neither AC or AC_ω is needed.
If every member of $X$ is a nonempty set, and the union $\bigcup X$ is well-ordered, then one may choose the least element of each member of $X$ . In this case, it was possible to simultaneously well-order every member of $X$ by making just one choice of a well-order of the union, so neither AC nor AC_ω was needed. (This example shows that the well-ordering theorem implies AC. The converse is also true, but less trivial.)

Choice function of a multivalued map

Given two sets X and Y, let F be a multivalued map from X to Y (equivalently, $F:X\rightarrow {\mathcal {P}}(Y)$ is a function from X to the power set of Y).

A function $f:X\rightarrow Y$ is said to be a selection of F, if:

\forall x\in X\,(f(x)\in F(x))\,.

The existence of more regular choice functions, namely continuous or measurable selections is important in the theory of differential inclusions, optimal control, and mathematical economics.^[2] See Selection theorem.

Bourbaki tau function

Nicolas Bourbaki used epsilon calculus for their foundations that had a $\tau$ symbol that could be interpreted as choosing an object (if one existed) that satisfies a given proposition. So if $P(x)$ is a predicate, then $\tau _{x}(P)$ is one particular object that satisfies $P$ (if one exists, otherwise it returns an arbitrary object). Hence we may obtain quantifiers from the choice function, for example $P(\tau _{x}(P))$ was equivalent to $(\exists x)(P(x))$ .^[3]

However, Bourbaki's choice operator is stronger than usual: it's a global choice operator. That is, it implies the axiom of global choice.^[4] Hilbert realized this when introducing epsilon calculus.^[5]

Notes

↑ Zermelo, Ernst (1904). "Beweis, dass jede Menge wohlgeordnet werden kann". Mathematische Annalen. 59 (4): 514–16. doi:10.1007/BF01445300.
↑ Border, Kim C. (1989). Fixed Point Theorems with Applications to Economics and Game Theory. Cambridge University Press. ISBN 0-521-26564-9.
↑ Bourbaki, Nicolas. Elements of Mathematics: Theory of Sets. ISBN 0-201-00634-0.
↑ John Harrison, "The Bourbaki View" eprint.
↑ "Here, moreover, we come upon a very remarkable circumstance, namely, that all of these transfinite axioms are derivable from a single axiom, one that also contains the core of one of the most attacked axioms in the literature of mathematics, namely, the axiom of choice: $A(a)\to A(\varepsilon (A))$ , where $\varepsilon$ is the transfinite logical choice function." Hilbert (1925), “On the Infinite”, excerpted in Jean van Heijenoort, From Frege to Gödel, p. 382. From nCatLab.

Related Research Articles

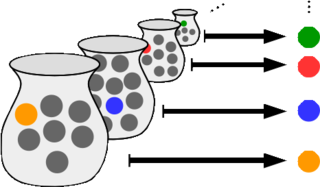
In mathematics, the axiom of choice, abbreviated AC or AoC, is an axiom of set theory equivalent to the statement that a Cartesian product of a collection of non-empty sets is non-empty. Informally put, the axiom of choice says that given any collection of sets, each containing at least one element, it is possible to construct a new set by choosing one element from each set, even if the collection is infinite. Formally, it states that for every indexed family $of nonempty sets, there exists an indexed set such that for every . The axiom of choice was formulated in 1904 by Ernst Zermelo in order to formalize his proof of the well-ordering theorem.$

<span class="mw-page-title-main">Transfinite induction</span> Mathematical concept

Transfinite induction is an extension of mathematical induction to well-ordered sets, for example to sets of ordinal numbers or cardinal numbers. Its correctness is a theorem of ZFC.

This is a glossary of some terms used in the branch of mathematics known as topology. Although there is no absolute distinction between different areas of topology, the focus here is on general topology. The following definitions are also fundamental to algebraic topology, differential topology and geometric topology.

In mathematics, the well-ordering theorem, also known as Zermelo's theorem, states that every set can be well-ordered. A set X is well-ordered by a strict total order if every non-empty subset of X has a least element under the ordering. The well-ordering theorem together with Zorn's lemma are the most important mathematical statements that are equivalent to the axiom of choice. Ernst Zermelo introduced the axiom of choice as an "unobjectionable logical principle" to prove the well-ordering theorem. One can conclude from the well-ordering theorem that every set is susceptible to transfinite induction, which is considered by mathematicians to be a powerful technique. One famous consequence of the theorem is the Banach–Tarski paradox.

Zorn's lemma, also known as the Kuratowski–Zorn lemma, is a proposition of set theory. It states that a partially ordered set containing upper bounds for every chain necessarily contains at least one maximal element.

In topology, a discrete space is a particularly simple example of a topological space or similar structure, one in which the points form a discontinuous sequence, meaning they are isolated from each other in a certain sense. The discrete topology is the finest topology that can be given on a set. Every subset is open in the discrete topology so that in particular, every singleton subset is an open set in the discrete topology.

In mathematics, a base (or basis; pl.: bases) for the topology $τ$ of a topological space $(X, τ)$ is a family $of open subsets of X such that every open set of the topology is equal to the union of some sub-family of . For example, the set of all open intervals in the real number line is a basis for the Euclidean topology on because every open interval is an open set, and also every open subset of can be written as a union of some family of open intervals.$

In mathematics, Tychonoff's theorem states that the product of any collection of compact topological spaces is compact with respect to the product topology. The theorem is named after Andrey Nikolayevich Tikhonov, who proved it first in 1930 for powers of the closed unit interval and in 1935 stated the full theorem along with the remark that its proof was the same as for the special case. The earliest known published proof is contained in a 1935 article by Tychonoff, "Über einen Funktionenraum".

In set theory, Zermelo–Fraenkel set theory, named after mathematicians Ernst Zermelo and Abraham Fraenkel, is an axiomatic system that was proposed in the early twentieth century in order to formulate a theory of sets free of paradoxes such as Russell's paradox. Today, Zermelo–Fraenkel set theory, with the historically controversial axiom of choice (AC) included, is the standard form of axiomatic set theory and as such is the most common foundation of mathematics. Zermelo–Fraenkel set theory with the axiom of choice included is abbreviated ZFC, where C stands for "choice", and ZF refers to the axioms of Zermelo–Fraenkel set theory with the axiom of choice excluded.

In mathematics, general topology is the branch of topology that deals with the basic set-theoretic definitions and constructions used in topology. It is the foundation of most other branches of topology, including differential topology, geometric topology, and algebraic topology.

Reverse mathematics is a program in mathematical logic that seeks to determine which axioms are required to prove theorems of mathematics. Its defining method can briefly be described as "going backwards from the theorems to the axioms", in contrast to the ordinary mathematical practice of deriving theorems from axioms. It can be conceptualized as sculpting out necessary conditions from sufficient ones.

In mathematics, two sets or classes A and B are equinumerous if there exists a one-to-one correspondence (or bijection) between them, that is, if there exists a function from A to B such that for every element y of B, there is exactly one element x of A with f(x) = y. Equinumerous sets are said to have the same cardinality (number of elements). The study of cardinality is often called equinumerosity (equalness-of-number). The terms equipollence (equalness-of-strength) and equipotence (equalness-of-power) are sometimes used instead.

The axiom of countable choice or axiom of denumerable choice, denoted AC_ω, is an axiom of set theory that states that every countable collection of non-empty sets must have a choice function. That is, given a function A with domain N (where N denotes the set of natural numbers) such that A(n) is a non-empty set for every n ∈ N, there exists a function f with domain N such that f(n) ∈ A(n) for every n ∈ N.

In mathematics, the axiom of dependent choice, denoted by $, is a weak form of the axiom of choice that is still sufficient to develop much of real analysis. It was introduced by Paul Bernays in a 1942 article that explores which set-theoretic axioms are needed to develop analysis.$

In mathematics, a set A is Dedekind-infinite if some proper subset B of A is equinumerous to A. Explicitly, this means that there exists a bijective function from A onto some proper subset B of A. A set is Dedekind-finite if it is not Dedekind-infinite. Proposed by Dedekind in 1888, Dedekind-infiniteness was the first definition of "infinite" that did not rely on the definition of the natural numbers.

In the mathematical discipline of set theory, there are many ways of describing specific countable ordinals. The smallest ones can be usefully and non-circularly expressed in terms of their Cantor normal forms. Beyond that, many ordinals of relevance to proof theory still have computable ordinal notations. However, it is not possible to decide effectively whether a given putative ordinal notation is a notation or not ; various more-concrete ways of defining ordinals that definitely have notations are available.

<span class="mw-page-title-main">Axiom of limitation of size</span>

In set theory, the axiom of limitation of size was proposed by John von Neumann in his 1925 axiom system for sets and classes. It formalizes the limitation of size principle, which avoids the paradoxes encountered in earlier formulations of set theory by recognizing that some classes are too big to be sets. Von Neumann realized that the paradoxes are caused by permitting these big classes to be members of a class. A class that is a member of a class is a set; a class that is not a set is a proper class. Every class is a subclass of V, the class of all sets. The axiom of limitation of size says that a class is a set if and only if it is smaller than V—that is, there is no function mapping it onto V. Usually, this axiom is stated in the equivalent form: A class is a proper class if and only if there is a function that maps it onto V.

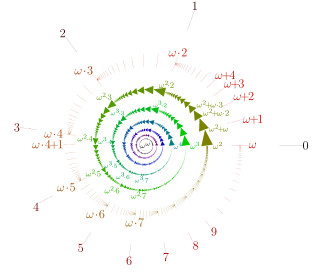
In set theory, an ordinal number, or ordinal, is a generalization of ordinal numerals aimed to extend enumeration to infinite sets.

This is a glossary of set theory.

The axiom of non-choice, also called axiom of unique choice, axiom of function choice or function comprehension principle is a function existence postulate. The difference to the axiom of choice is that in the antecedent, the existence of $is already granted to be unique for each .$

References

This article incorporates material from Choice function on PlanetMath, which is licensed under the Creative Commons Attribution/Share-Alike License.

This page is based on this Wikipedia article
Text is available under the CC BY-SA 4.0 license; additional terms may apply.
Images, videos and audio are available under their respective licenses.

[Zermelo,_1904-1] Zermelo, Ernst (1904). "Beweis, dass jede Menge wohlgeordnet werden kann". Mathematische Annalen. 59 (4): 514–16. doi:10.1007/BF01445300.

[2] Border, Kim C. (1989). Fixed Point Theorems with Applications to Economics and Game Theory. Cambridge University Press. ISBN 0-521-26564-9.

[3] Bourbaki, Nicolas. Elements of Mathematics: Theory of Sets. ISBN 0-201-00634-0.

[4] John Harrison, "The Bourbaki View" eprint.

[5] "Here, moreover, we come upon a very remarkable circumstance, namely, that all of these transfinite axioms are derivable from a single axiom, one that also contains the core of one of the most attacked axioms in the literature of mathematics, namely, the axiom of choice: $A(a)\to A(\varepsilon (A))$ , where $\varepsilon$ is the transfinite logical choice function." Hilbert (1925), “On the Infinite”, excerpted in Jean van Heijenoort, From Frege to Gödel, p. 382. From nCatLab.

[1]

[2]

[3]

[4]

[5]