The circle of equal altitude, also called circle of position (CoP), is defined as the locus of points on Earth on which an observer sees a celestial object such as the sun or a star, at a given time, with the same observed altitude. It was discovered by the American sea-captain Thomas Hubbard Sumner in 1837, published in 1843 and is the basis of an important method in celestial navigation.
Sumner discovered the line on a voyage from South Carolina to Greenock in Scotland in 1837. On December 17, as he was nearing the coast of Wales, he was uncertain of his position after several days of cloudy weather and no sights. A momentary opening in the clouds allowed him to determine the altitude of the sun. This, together with the chronometer time and the latitude enabled him to calculate the longitude. But he was not confident of his latitude, which depended on dead reckoning (DR). So he calculated longitude using his DR value and two more values of latitude 10' and 20' to the north. He found that the three positions were on a straight line which happened to pass through Smalls Lighthouse. He realised that he must be located somewhere on that line and that if he set course E.N.E. along the line he should eventually sight the Smalls Light which, in fact he did, in less than an hour. Having found the line empirically, he then worked out the theory, and published this in a book in 1843. The method was quickly recognized as an important development in celestial navigation, and was made available to every ship in the United States Navy. [1]
The center of the CoP, is the geographical position (GP) of the observed body, the substellar point for a star, the subsolar point for the sun. The radius is the great circle distance equal to the zenith distance of the body.
As the circles used for navigation generally have a radius of thousands of miles, a segment a few tens of miles long closely approximates a straight line, as described in Sumner's original use of the method.
The equation links the following variables [2]
Being B the latitude (+N/-S), L the longitude (+E/-W). LHA = GHA + L is the local hour angle (+W/-E), Dec and GHA are the declination and Greenwich hour angle of the star observed. And Ho is the true or observed altitude, that is, the altitude measured with a sextant corrected for dip, refraction and parallax.
In geography, latitude is a coordinate that specifies the north–south position of a point on the surface of the Earth or another celestial body. Latitude is given as an angle that ranges from −90° at the south pole to 90° at the north pole, with 0° at the Equator. Lines of constant latitude, or parallels, run east–west as circles parallel to the equator. Latitude and longitude are used together as a coordinate pair to specify a location on the surface of the Earth.
Longitude is a geographic coordinate that specifies the east–west position of a point on the surface of the Earth, or another celestial body. It is an angular measurement, usually expressed in degrees and denoted by the Greek letter lambda (λ). Meridians are imaginary semicircular lines running from pole to pole that connect points with the same longitude. The prime meridian defines 0° longitude; by convention the International Reference Meridian for the Earth passes near the Royal Observatory in Greenwich, south-east London on the island of Great Britain. Positive longitudes are east of the prime meridian, and negative ones are west.
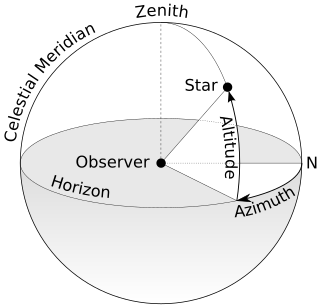
An azimuth is the horizontal angle from a cardinal direction, most commonly north, in a local or observer-centric spherical coordinate system.
In astronomy, coordinate systems are used for specifying positions of celestial objects relative to a given reference frame, based on physical reference points available to a situated observer. Coordinate systems in astronomy can specify an object's relative position in three-dimensional space or plot merely by its direction on a celestial sphere, if the object's distance is unknown or trivial.
In astronomy and celestial navigation, the hour angle is the dihedral angle between the meridian plane and the hour circle.
A sundial is a horological device that tells the time of day when direct sunlight shines by the apparent position of the Sun in the sky. In the narrowest sense of the word, it consists of a flat plate and a gnomon, which casts a shadow onto the dial. As the Sun appears to move through the sky, the shadow aligns with different hour-lines, which are marked on the dial to indicate the time of day. The style is the time-telling edge of the gnomon, though a single point or nodus may be used. The gnomon casts a broad shadow; the shadow of the style shows the time. The gnomon may be a rod, wire, or elaborately decorated metal casting. The style must be parallel to the axis of the Earth's rotation for the sundial to be accurate throughout the year. The style's angle from horizontal is equal to the sundial's geographical latitude.
In geometry, a solid angle is a measure of the amount of the field of view from some particular point that a given object covers. That is, it is a measure of how large the object appears to an observer looking from that point. The point from which the object is viewed is called the apex of the solid angle, and the object is said to subtend its solid angle at that point.
Celestial navigation, also known as astronavigation, is the practice of position fixing using stars and other celestial bodies that enables a navigator to accurately determine their actual current physical position in space or on the surface of the Earth without relying solely on estimated positional calculations, commonly known as dead reckoning. Celestial navigation is performed without using satellite navigation or other similar modern electronic or digital positioning means.
In navigation, a rhumb line, rhumb, or loxodrome is an arc crossing all meridians of longitude at the same angle, that is, a path with constant azimuth . Navigation on a fixed course would result in a rhumb-line track.
The great-circle distance, orthodromic distance, or spherical distance is the distance between two points on a sphere, measured along the great-circle arc between them. This arc is the shortest path between the two points on the surface of the sphere.
The haversine formula determines the great-circle distance between two points on a sphere given their longitudes and latitudes. Important in navigation, it is a special case of a more general formula in spherical trigonometry, the law of haversines, that relates the sides and angles of spherical triangles.
In astronomical navigation, the intercept method, also known as Marcq St. Hilaire method, is a method of calculating an observer's position on Earth (geopositioning). It was originally called the azimuth intercept method because the process involves drawing a line which intercepts the azimuth line. This name was shortened to intercept method and the intercept distance was shortened to 'intercept'.
Longitude by chronometer is a method, in navigation, of determining longitude using a marine chronometer, which was developed by John Harrison during the first half of the eighteenth century. It is an astronomical method of calculating the longitude at which a position line, drawn from a sight by sextant of any celestial body, crosses the observer's assumed latitude. In order to calculate the position line, the time of the sight must be known so that the celestial position i.e. the Greenwich Hour Angle and Declination, of the observed celestial body is known. All that can be derived from a single sight is a single position line, which can be achieved at any time during daylight when both the sea horizon and the sun are visible. To achieve a fix, more than one celestial body and the sea horizon must be visible. This is usually only possible at dawn and dusk.
Ex-meridian is a celestial navigation method of calculating an observer's position on Earth. The method gives the observer a position line on which the observer is situated. It is usually used when the Sun is obscured at noon, and as a result, a meridian altitude is not possible. The navigator measures the altitude of the Sun as close to noon as possible and then calculates where the position line lies.
Angular distance or angular separation is the measure of the angle between the orientation of two straight lines, rays, or vectors in three-dimensional space, or the central angle subtended by the radii through two points on a sphere. When the rays are lines of sight from an observer to two points in space, it is known as the apparent distance or apparent separation.
Thomas Hubbard Sumner was a sea captain during the 19th century. He is best known for developing the celestial navigation method known as the Sumner line or circle of equal altitude.
The navigational algorithms are the quintessence of the executable software on portable calculators or smartphones as an aid to the art of navigation, this attempt article describe both algorithms and software for smartphones implementing different calculation procedures for navigation. The calculation power obtained by the languages—Basic, C, Java, etc.—from portable calculators or smartphones, has made it possible to develop programs that allow calculating the position without the need for tables, in fact they have some basic tables with the correction factors for each year and calculate the values "on the fly" at runtime.
The position of the Sun in the sky is a function of both the time and the geographic location of observation on Earth's surface. As Earth orbits the Sun over the course of a year, the Sun appears to move with respect to the fixed stars on the celestial sphere, along a circular path called the ecliptic.
In astronavigation, sight reduction is the process of deriving from a sight the information needed for establishing a line of position, generally by intercept method.
The isoazimuth is the locus of the points on the Earth's surface whose initial orthodromic course with respect to a fixed point is constant.
