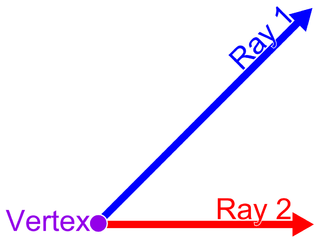
In plane geometry, an angle is the figure formed by two rays, called the sides of the angle, sharing a common endpoint, called the vertex of the angle. Angles formed by two rays lie in a plane, but this plane does not have to be a Euclidean plane. Angles are also formed by the intersection of two planes in Euclidean and other spaces. These are called dihedral angles. Angles formed by the intersection of two curves in a plane are defined as the angle determined by the tangent rays at the point of intersection. Similar statements hold in space, for example, the spherical angle formed by two great circles on a sphere is the dihedral angle between the planes determined by the great circles.
A centripetal force is a force that makes a body follow a curved path. Its direction is always orthogonal to the motion of the body and towards the fixed point of the instantaneous center of curvature of the path. Isaac Newton described it as "a force by which bodies are drawn or impelled, or in any way tend, towards a point as to a centre". In Newtonian mechanics, gravity provides the centripetal force responsible for astronomical orbits.

In mathematics, curvature is any of a number of loosely related concepts in different areas of geometry. Intuitively, curvature is the amount by which a geometric object such as a surface deviates from being a flat plane, or a curve from being straight as in the case of a line, but this is defined in different ways depending on the context. There is a key distinction between extrinsic curvature, which is defined for objects embedded in another space – in a way that relates to the radius of curvature of circles that touch the object – and intrinsic curvature, which is defined in terms of the lengths of curves within a Riemannian manifold.

Angular displacement of a body is the angle in radians through which a point revolves around a centre or line has been rotated in a specified sense about a specified axis. When a body rotates about its axis, the motion cannot simply be analyzed as a particle, as in circular motion it undergoes a changing velocity and acceleration at any time (t). When dealing with the rotation of a body, it becomes simpler to consider the body itself rigid. A body is generally considered rigid when the separations between all the particles remains constant throughout the body's motion, so for example parts of its mass are not flying off. In a realistic sense, all things can be deformable, however this impact is minimal and negligible. Thus the rotation of a rigid body over a fixed axis is referred to as rotational motion.
An orthogonal matrix is a square matrix whose columns and rows are orthogonal unit vectors, i.e.

In mathematics, a unit vector in a normed vector space is a vector of length 1. A unit vector is often denoted by a lowercase letter with a circumflex, or "hat": . The term direction vector is used to describe a unit vector being used to represent spatial direction, and such quantities are commonly denoted as d. Two 2D direction vectors, d1 and d2 are illustrated. 2D spatial directions represented this way are numerically equivalent to points on the unit circle.
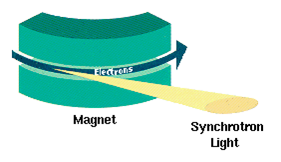
Synchrotron radiation is the electromagnetic radiation emitted when charged particles are accelerated radially, i.e., when they are subject to an acceleration perpendicular to their velocity. It is produced, for example, in synchrotrons using bending magnets, undulators and/or wigglers. If the particle is non-relativistic, then the emission is called cyclotron emission. If, on the other hand, the particles are relativistic, sometimes referred to as ultrarelativistic, the emission is called synchrotron emission. Synchrotron radiation may be achieved artificially in synchrotrons or storage rings, or naturally by fast electrons moving through magnetic fields. The radiation produced in this way has a characteristic polarization and the frequencies generated can range over the entire electromagnetic spectrum which is also called continuum radiation.
In mechanics and geometry, the 3D rotation group, often denoted SO(3), is the group of all rotations about the origin of three-dimensional Euclidean space R3 under the operation of composition. By definition, a rotation about the origin is a transformation that preserves the origin, Euclidean distance, and orientation. Every non-trivial rotation is determined by its axis of rotation and its angle of rotation. Composing two rotations results in another rotation; every rotation has a unique inverse rotation; and the identity map satisfies the definition of a rotation. Owing to the above properties, the set of all rotations is a group under composition. Rotations are not commutative, making it a nonabelian group. Moreover, the rotation group has a natural structure as a manifold for which the group operations are smoothly differentiable; so it is in fact a Lie group. It is compact and has dimension 3.
In the mathematical field of differential geometry, a metric tensor is a type of function which takes as input a pair of tangent vectors v and w at a point of a surface and produces a real number scalar g(v, w) in a way that generalizes many of the familiar properties of the dot product of vectors in Euclidean space. In the same way as a dot product, metric tensors are used to define the length of and angle between tangent vectors. Through integration, the metric tensor allows one to define and compute the length of curves on the manifold.

Scalar potential, simply stated, describes the situation where the difference in the potential energies of an object in two different positions depends only on the positions, not upon the path taken by the object in traveling from one position to the other. It is a scalar field in three-space: a directionless value (scalar) that depends only on its location. A familiar example is potential energy due to gravity.

In geometry, a (general) conical surface is the unbounded surface formed by the union of all the straight lines that pass through a fixed point — the apex or vertex — and any point of some fixed space curve — the directrix — that does not contain the apex. Each of those lines is called a generatrix of the surface.

A cone is a three-dimensional geometric shape that tapers smoothly from a flat base to a point called the apex or vertex.

In relativistic physics, a velocity-addition formula is a three-dimensional equation that relates the velocities of objects in different reference frames. Such formulas apply to successive Lorentz transformations, so they also relate different frames. Accompanying velocity addition is a kinematic effect known as Thomas precession, whereby successive non-collinear Lorentz boosts become equivalent to the composition of a rotation of the coordinate system and a boost.

Arc length is the distance between two points along a section of a curve.
In geometry, various formalisms exist to express a rotation in three dimensions as a mathematical transformation. In physics, this concept is applied to classical mechanics where rotational kinematics is the science of quantitative description of a purely rotational motion. The orientation of an object at a given instant is described with the same tools, as it is defined as an imaginary rotation from a reference placement in space, rather than an actually observed rotation from a previous placement in space.
In the differential geometry of surfaces, a Darboux frame is a natural moving frame constructed on a surface. It is the analog of the Frenet–Serret frame as applied to surface geometry. A Darboux frame exists at any non-umbilic point of a surface embedded in Euclidean space. It is named after French mathematician Jean Gaston Darboux.

In inversive geometry, an inverse curve of a given curve C is the result of applying an inverse operation to C. Specifically, with respect to a fixed circle with center O and radius k the inverse of a point Q is the point P for which P lies on the ray OQ and OP·OQ = k2. The inverse of the curve C is then the locus of P as Q runs over C. The point O in this construction is called the center of inversion, the circle the circle of inversion, and k the radius of inversion.

In celestial mechanics, a Kepler orbit is the motion of one body relative to another, as an ellipse, parabola, or hyperbola, which forms a two-dimensional orbital plane in three-dimensional space. It considers only the point-like gravitational attraction of two bodies, neglecting perturbations due to gravitational interactions with other objects, atmospheric drag, solar radiation pressure, a non-spherical central body, and so on. It is thus said to be a solution of a special case of the two-body problem, known as the Kepler problem. As a theory in classical mechanics, it also does not take into account the effects of general relativity. Keplerian orbits can be parametrized into six orbital elements in various ways.
In fluid dynamics, the Oseen equations describe the flow of a viscous and incompressible fluid at small Reynolds numbers, as formulated by Carl Wilhelm Oseen in 1910. Oseen flow is an improved description of these flows, as compared to Stokes flow, with the (partial) inclusion of convective acceleration.
A proper reference frame in the theory of relativity is a particular form of accelerated reference frame, that is, a reference frame in which an accelerated observer can be considered as being at rest. It can describe phenomena in curved spacetime, as well as in "flat" Minkowski spacetime in which the spacetime curvature caused by the energy-momentum tensor can be disregarded. Since this article considers only flat spacetime—and uses the definition that special relativity is the theory of flat spacetime while general relativity is a theory of gravitation in terms of curved spacetime—it is consequently concerned with accelerated frames in special relativity.