In physics, the cross section is a measure of the probability that a specific process will take place in a collision of two particles. For example, the Rutherford cross-section is a measure of probability that an alpha particle will be deflected by a given angle during an interaction with an atomic nucleus. Cross section is typically denoted σ (sigma) and is expressed in units of area, more specifically in barns. In a way, it can be thought of as the size of the object that the excitation must hit in order for the process to occur, but more exactly, it is a parameter of a stochastic process.

In physics, the Maxwell–Boltzmann distribution, or Maxwell(ian) distribution, is a particular probability distribution named after James Clerk Maxwell and Ludwig Boltzmann.

In mathematical analysis, the Dirac delta function, also known as the unit impulse, is a generalized function on the real numbers, whose value is zero everywhere except at zero, and whose integral over the entire real line is equal to one. Since there is no function having this property, modelling the delta "function" rigorously involves the use of limits or, as is common in mathematics, measure theory and the theory of distributions.

A drop or droplet is a small column of liquid, bounded completely or almost completely by free surfaces. A drop may form when liquid accumulates at the end of a tube or other surface boundary, producing a hanging drop called a pendant drop. Drops may also be formed by the condensation of a vapor or by atomization of a larger mass of solid. Water vapor will condense into droplets depending on the temperature. The temperature at which droplets form is called the dew point.
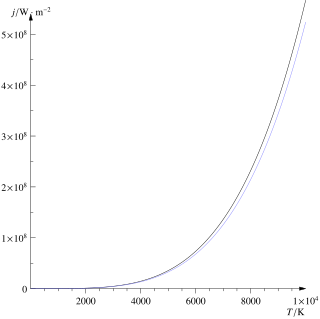
The Stefan–Boltzmann law, also known as Stefan's law, describes the intensity of the thermal radiation emitted by matter in terms of that matter's temperature. It is named for Josef Stefan, who empirically derived the relationship, and Ludwig Boltzmann who derived the law theoretically.

An aerosol is a suspension of fine solid particles or liquid droplets in air or another gas. Aerosols can be generated from natural or human causes. The term aerosol commonly refers to the mixture of particulates in air, and not to the particulate matter alone. Examples of natural aerosols are fog, mist or dust. Examples of human caused aerosols include particulate air pollutants, mist from the discharge at hydroelectric dams, irrigation mist, perfume from atomizers, smoke, dust, sprayed pesticides, and medical treatments for respiratory illnesses.

A Fourier series is an expansion of a periodic function into a sum of trigonometric functions. The Fourier series is an example of a trigonometric series, but not all trigonometric series are Fourier series. By expressing a function as a sum of sines and cosines, many problems involving the function become easier to analyze because trigonometric functions are well understood. For example, Fourier series were first used by Joseph Fourier to find solutions to the heat equation. This application is possible because the derivatives of trigonometric functions fall into simple patterns. Fourier series cannot be used to approximate arbitrary functions, because most functions have infinitely many terms in their Fourier series, and the series do not always converge. Well-behaved functions, for example smooth functions, have Fourier series that converge to the original function. The coefficients of the Fourier series are determined by integrals of the function multiplied by trigonometric functions, described in Common forms of the Fourier series below.
In fluid dynamics, Stokes' law is an empirical law for the frictional force – also called drag force – exerted on spherical objects with very small Reynolds numbers in a viscous fluid. It was derived by George Gabriel Stokes in 1851 by solving the Stokes flow limit for small Reynolds numbers of the Navier–Stokes equations.

In electromagnetism, the Mie solution to Maxwell's equations describes the scattering of an electromagnetic plane wave by a homogeneous sphere. The solution takes the form of an infinite series of spherical multipole partial waves. It is named after German physicist Gustav Mie.
In mathematics, the Poisson summation formula is an equation that relates the Fourier series coefficients of the periodic summation of a function to values of the function's continuous Fourier transform. Consequently, the periodic summation of a function is completely defined by discrete samples of the original function's Fourier transform. And conversely, the periodic summation of a function's Fourier transform is completely defined by discrete samples of the original function. The Poisson summation formula was discovered by Siméon Denis Poisson and is sometimes called Poisson resummation.
Directional statistics is the subdiscipline of statistics that deals with directions, axes or rotations in Rn. More generally, directional statistics deals with observations on compact Riemannian manifolds including the Stiefel manifold.
In particle physics, a shower is a cascade of secondary particles produced as the result of a high-energy particle interacting with dense matter. The incoming particle interacts, producing multiple new particles with lesser energy; each of these then interacts, in the same way, a process that continues until many thousands, millions, or even billions of low-energy particles are produced. These are then stopped in the matter and absorbed.
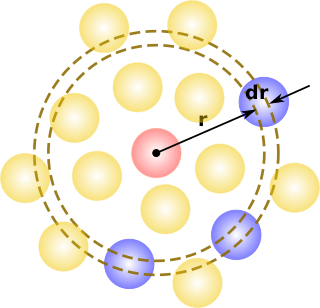
In statistical mechanics, the radial distribution function, in a system of particles, describes how density varies as a function of distance from a reference particle.

The Jeans instability is a concept in astrophysics that describes an instability that leads to the gravitational collapse of a cloud of gas or dust. It causes the collapse of interstellar gas clouds and subsequent star formation. It occurs when the internal gas pressure is not strong enough to prevent the gravitational collapse of a region filled with matter. It is named after James Jeans.
The Kelvin equation describes the change in vapour pressure due to a curved liquid–vapor interface, such as the surface of a droplet. The vapor pressure at a convex curved surface is higher than that at a flat surface. The Kelvin equation is dependent upon thermodynamic principles and does not allude to special properties of materials. It is also used for determination of pore size distribution of a porous medium using adsorption porosimetry. The equation is named in honor of William Thomson, also known as Lord Kelvin.
Mean inter-particle distance is the mean distance between microscopic particles in a macroscopic body.

The feet of geckos have a number of specializations. Their surfaces can adhere to any type of material with the exception of Teflon (PTFE). This phenomenon can be explained with three elements:
Classical nucleation theory (CNT) is the most common theoretical model used to quantitatively study the kinetics of nucleation.
The raindrop size distribution (DSD), or granulometry of rain, is the distribution of the number of raindrops according to their diameter (D). Three processes account for the formation of drops: water vapor condensation, accumulation of small drops on large drops and collisions between sizes. According to the time spent in the cloud, the vertical movement in it and the ambient temperature, the drops that have a very varied history and a distribution of diameters from a few micrometers to a few millimeters.











