This page is based on this
Wikipedia article Text is available under the
CC BY-SA 4.0 license; additional terms may apply.
Images, videos and audio are available under their respective licenses.

In geometry, an octahedron is a polyhedron with eight faces, twelve edges, and six vertices. The term is most commonly used to refer to the regular octahedron, a Platonic solid composed of eight equilateral triangles, four of which meet at each vertex.
A polyhedral compound is a figure that is composed of several polyhedra sharing a common centre. They are the three-dimensional analogs of polygonal compounds such as the hexagram.
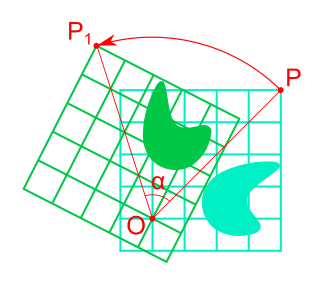
Rotation in mathematics is a concept originating in geometry. Any rotation is a motion of a certain space that preserves at least one point. It can describe, for example, the motion of a rigid body around a fixed point. A rotation is different from other types of motions: translations, which have no fixed points, and (hyperplane) reflections, each of them having an entire (n − 1)-dimensional flat of fixed points in a n-dimensional space. A clockwise rotation is a negative magnitude so a counterclockwise turn has a positive magnitude.
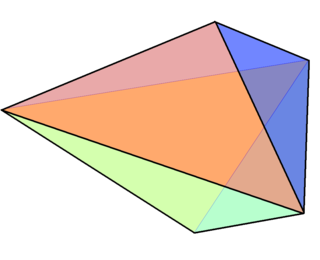
In geometry, the triangular bipyramid is a type of hexahedron, being the first in the infinite set of face-transitive bipyramids. It is the dual of the triangular prism with 6 isosceles triangle faces.

In chemistry, octahedral molecular geometry describes the shape of compounds with six atoms or groups of atoms or ligands symmetrically arranged around a central atom, defining the vertices of an octahedron. The octahedron has eight faces, hence the prefix octa. The octahedron is one of the Platonic solids, although octahedral molecules typically have an atom in their centre and no bonds between the ligand atoms. A perfect octahedron belongs to the point group Oh. Examples of octahedral compounds are sulfur hexafluoride SF6 and molybdenum hexacarbonyl Mo(CO)6. The term "octahedral" is used somewhat loosely by chemists, focusing on the geometry of the bonds to the central atom and not considering differences among the ligands themselves. For example, [Co(NH3)6]3+, which is not octahedral in the mathematical sense due to the orientation of the N-H bonds, is referred to as octahedral.
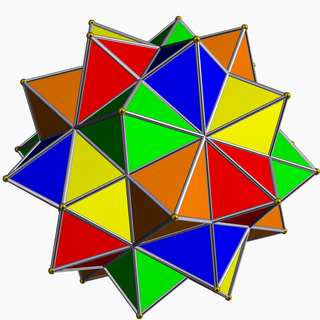
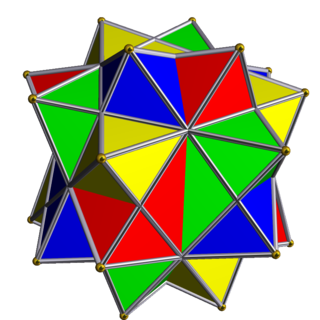
The compound of five octahedra is one of the five regular polyhedron compounds. This polyhedron can be seen as either a polyhedral stellation or a compound. This compound was first described by Edmund Hess in 1876. It is unique among the regular compounds for not having a regular convex hull.
Rigid unit modes (RUMs) represent a class of lattice vibrations or phonons that exist in network materials such as quartz, cristobalite or zirconium tungstate. Network materials can be described as three-dimensional networks of polyhedral groups of atoms such as SiO4 tetrahedra or TiO6 octahedra. A RUM is a lattice vibration in which the polyhedra are able to move, by translation and/or rotation, without distorting. RUMs in crystalline materials are the counterparts of floppy modes in glasses, as introduced by Jim Phillips and Mike Thorpe.
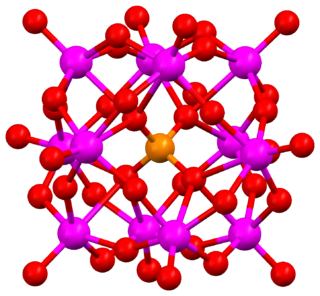
Keggin structure is the best known structural form for heteropoly acids. It is the structural form of α-Keggin anions, which have a general formula of [XM12O40]n−, where X is the heteroatom (most commonly are P5+, Si4+, or B3+), M is the addenda atom (most common are molybdenum and tungsten), and O represents oxygen. The structure self-assembles in acidic aqueous solution and is the most stable structure of polyoxometalate catalysts.
Dioxygenyl hexafluoroplatinate is a compound with formula O2PtF6. It is a hexafluoroplatinate of the unusual dioxygenyl cation, O2+, and is the first known compound containing this cation. It can be produced by the reaction of dioxygen with platinum hexafluoride. The fact that PtF
6 is strong enough to oxidise O
2, whose first ionization potential is 12.2 eV, led Neil Bartlett to correctly surmise that it might be able to oxidise xenon (first ionization potential 12.13 eV). This led to the discovery of xenon hexafluoroplatinate, which proved that the noble gases, previously thought to be inert, are able to form chemical compounds.
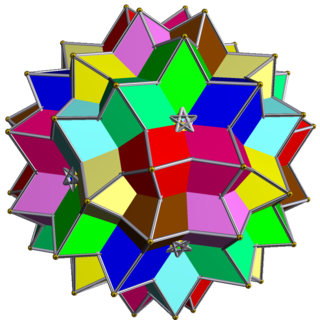
These uniform polyhedron compounds are symmetric arrangements of 10 octahedra, considered as triangular antiprisms, aligned with the axes of three-fold rotational symmetry of an icosahedron. The two compounds differ in the orientation of their octahedra: each compound may be transformed into the other by rotating each octahedron by 60 degrees.

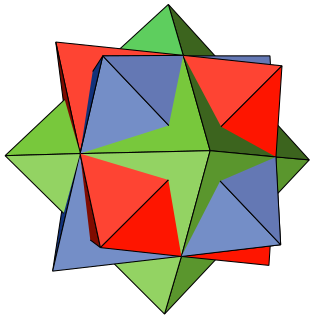
This uniform polyhedron compound is a symmetric arrangement of 8 octahedra, considered as triangular antiprisms. It can be constructed by superimposing eight identical octahedra, and then rotating them in pairs about the four axes that pass through the centres of two opposite octahedral faces. Each octahedron is rotated by an equal angle θ.

In geometry, a Bricard octahedron is a member of a family of flexible polyhedra constructed by Raoul Bricard in 1897.
That is, it is possible for the overall shape of this polyhedron to change in a continuous motion, without any changes to the lengths of its edges nor to the shapes of its faces.
These octahedra were the first flexible polyhedra to be discovered.

In engineering, a mechanism is a device that transforms input forces and movement into a desired set of output forces and movement. Mechanisms generally consist of moving components that can include: