In mathematics, a spherical coordinate system is a coordinate system for three-dimensional space where the position of a given point in space is specified by three real numbers: the radial distancer along the radial line connecting the point to the fixed point of origin; the polar angleθ between the radial line and a given polar axis; and the azimuthal angleφ as the angle of rotation of the radial line around the polar axis. (See graphic regarding the "physics convention".) Once the radius is fixed, the three coordinates (r, θ, φ), known as a 3-tuple, provide a coordinate system on a sphere, typically called the spherical polar coordinates. The plane passing through the origin and perpendicular to the polar axis (where the polar angle is a right angle) is called the reference plane (sometimes fundamental plane).
In geometry, a tetrahedron, also known as a triangular pyramid, is a polyhedron composed of four triangular faces, six straight edges, and four vertices. The tetrahedron is the simplest of all the ordinary convex polyhedra.
In mechanics and geometry, the 3D rotation group, often denoted SO(3), is the group of all rotations about the origin of three-dimensional Euclidean space under the operation of composition.

The Euler angles are three angles introduced by Leonhard Euler to describe the orientation of a rigid body with respect to a fixed coordinate system.
The Kerr metric or Kerr geometry describes the geometry of empty spacetime around a rotating uncharged axially symmetric black hole with a quasispherical event horizon. The Kerr metric is an exact solution of the Einstein field equations of general relativity; these equations are highly non-linear, which makes exact solutions very difficult to find.
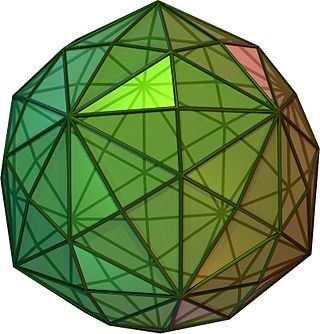
In geometry, a disdyakis triacontahedron, hexakis icosahedron, decakis dodecahedron, kisrhombic triacontahedron or d120 is a Catalan solid with 120 faces and the dual to the Archimedean truncated icosidodecahedron. As such it is face-uniform but with irregular face polygons. It slightly resembles an inflated rhombic triacontahedron: if one replaces each face of the rhombic triacontahedron with a single vertex and four triangles in a regular fashion, one ends up with a disdyakis triacontahedron. That is, the disdyakis triacontahedron is the Kleetope of the rhombic triacontahedron. It is also the barycentric subdivision of the regular dodecahedron and icosahedron. It has the most faces among the Archimedean and Catalan solids, with the snub dodecahedron, with 92 faces, in second place.
In linear algebra, a rotation matrix is a transformation matrix that is used to perform a rotation in Euclidean space. For example, using the convention below, the matrix

The Stokes parameters are a set of values that describe the polarization state of electromagnetic radiation. They were defined by George Gabriel Stokes in 1851, as a mathematically convenient alternative to the more common description of incoherent or partially polarized radiation in terms of its total intensity (I), (fractional) degree of polarization (p), and the shape parameters of the polarization ellipse. The effect of an optical system on the polarization of light can be determined by constructing the Stokes vector for the input light and applying Mueller calculus, to obtain the Stokes vector of the light leaving the system. They can be determined from directly observable phenomena. The original Stokes paper was discovered independently by Francis Perrin in 1942 and by Subrahamanyan Chandrasekhar in 1947, who named it as the Stokes parameters.

In geometry, a rhombohedron is a special case of a parallelepiped in which all six faces are congruent rhombi. It can be used to define the rhombohedral lattice system, a honeycomb with rhombohedral cells. A rhombohedron has two opposite apices at which all face angles are equal; a prolate rhombohedron has this common angle acute, and an oblate rhombohedron has an obtuse angle at these vertices. A cube is a special case of a rhombohedron with all sides square.
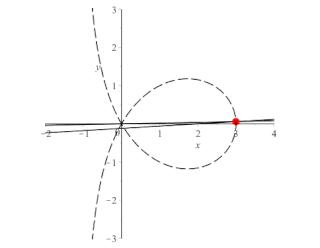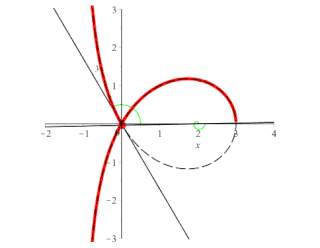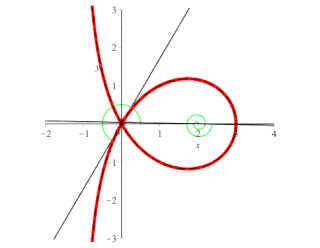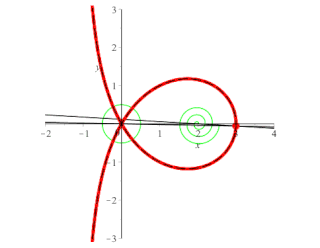
In algebraic geometry, the trisectrix of Maclaurin is a cubic plane curve notable for its trisectrix property, meaning it can be used to trisect an angle. It can be defined as locus of the point of intersection of two lines, each rotating at a uniform rate about separate points, so that the ratio of the rates of rotation is 1:3 and the lines initially coincide with the line between the two points. A generalization of this construction is called a sectrix of Maclaurin. The curve is named after Colin Maclaurin who investigated the curve in 1742.

In statistics, Procrustes analysis is a form of statistical shape analysis used to analyse the distribution of a set of shapes. The name Procrustes refers to a bandit from Greek mythology who made his victims fit his bed either by stretching their limbs or cutting them off.
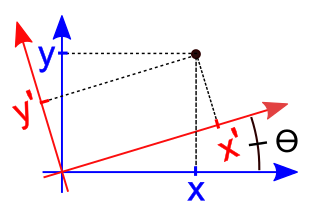
In mathematics, a rotation of axes in two dimensions is a mapping from an xy-Cartesian coordinate system to an x′y′-Cartesian coordinate system in which the origin is kept fixed and the x′ and y′ axes are obtained by rotating the x and y axes counterclockwise through an angle . A point P has coordinates (x, y) with respect to the original system and coordinates (x′, y′) with respect to the new system. In the new coordinate system, the point P will appear to have been rotated in the opposite direction, that is, clockwise through the angle . A rotation of axes in more than two dimensions is defined similarly. A rotation of axes is a linear map and a rigid transformation.
In geometry, various formalisms exist to express a rotation in three dimensions as a mathematical transformation. In physics, this concept is applied to classical mechanics where rotational kinematics is the science of quantitative description of a purely rotational motion. The orientation of an object at a given instant is described with the same tools, as it is defined as an imaginary rotation from a reference placement in space, rather than an actually observed rotation from a previous placement in space.

This uniform polyhedron compound is a symmetric arrangement of 6 cubes, considered as square prisms. It can be constructed by superimposing six identical cubes, and then rotating them in pairs about the three axes that pass through the centres of two opposite cubic faces. Each cube is rotated by an equal angle θ.

This uniform polyhedron compound is a symmetric arrangement of 12 tetrahedra, considered as antiprisms. It can be constructed by superimposing six identical copies of the stella octangula, and then rotating them in pairs about the three axes that pass through the centres of two opposite cubic faces. Each stella octangula is rotated by an equal angle θ. Equivalently, a stella octangula may be inscribed within each cube in the compound of six cubes with rotational freedom, which has the same vertices as this compound.
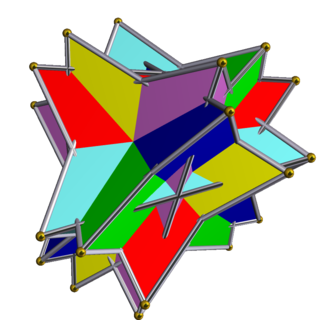
The compound of six tetrahedra with rotational freedom is a uniform polyhedron compound made of a symmetric arrangement of 6 tetrahedra, considered as antiprisms. It can be constructed by superimposing six tetrahedra within a cube, and then rotating them in pairs about the three axes that pass through the centres of two opposite cubic faces. Each tetrahedron is rotated by an equal angle θ. Equivalently, a tetrahedron may be inscribed within each cube in the compound of six cubes with rotational freedom, in such a way as to preserve tetrahedral symmetry.
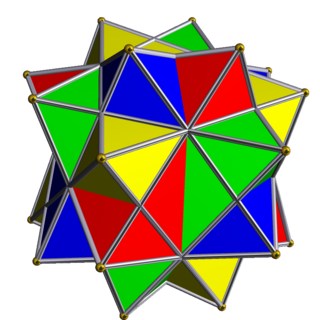
The compound of four octahedra with rotational freedom is a uniform polyhedron compound. It consists in a symmetric arrangement of 4 octahedra, considered as triangular antiprisms. It can be constructed by superimposing four identical octahedra, and then rotating each by an equal angle θ about a separate axis passing through the centres of two opposite octahedral faces, in such a way as to preserve pyritohedral symmetry.

The compound of twenty octahedra with rotational freedom is a uniform polyhedron compound. It's composed of a symmetric arrangement of 20 octahedra, considered as triangular antiprisms. It can be constructed by superimposing two copies of the compound of 10 octahedra UC16, and for each resulting pair of octahedra, rotating each octahedron in the pair by an equal and opposite angle θ.

This uniform polyhedron compound is a symmetric arrangement of 12 pentagonal antiprisms. It can be constructed by inscribing one pair of pentagonal antiprisms within an icosahedron, in each of the six possible ways, and then rotating each by an equal and opposite angle θ.
The direct-quadrature-zerotransformation or zero-direct-quadraturetransformation is a tensor that rotates the reference frame of a three-element vector or a three-by-three element matrix in an effort to simplify analysis. The DQZ transform is the product of the Clarke transform and the Park transform, first proposed in 1929 by Robert H. Park.