Related Research Articles
A cuboctahedron is a polyhedron with 8 triangular faces and 6 square faces. A cuboctahedron has 12 identical vertices, with 2 triangles and 2 squares meeting at each, and 24 identical edges, each separating a triangle from a square. As such, it is a quasiregular polyhedron, i.e. an Archimedean solid that is not only vertex-transitive but also edge-transitive. It is radially equilateral.
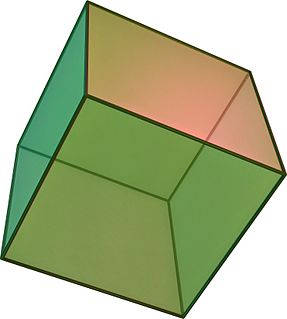
In geometry, a cube is a three-dimensional solid object bounded by six square faces, facets or sides, with three meeting at each vertex.
In geometry, a regular icosahedron is a convex polyhedron with 20 faces, 30 edges and 12 vertices. It is one of the five Platonic solids, and the one with the most faces.
In geometry, an octahedron is a polyhedron with eight faces. The term is most commonly used to refer to the regular octahedron, a Platonic solid composed of eight equilateral triangles, four of which meet at each vertex.
A polyhedral compound is a figure that is composed of several polyhedra sharing a common centre. They are the three-dimensional analogs of polygonal compounds such as the hexagram.
In geometry, the rhombic dodecahedron is a convex polyhedron with 12 congruent rhombic faces. It has 24 edges, and 14 vertices of 2 types. It is a Catalan solid, and the dual polyhedron of the cuboctahedron.
In geometry, a tetrakis hexahedron is a Catalan solid. Its dual is the truncated octahedron, an Archimedean solid.
In geometry, the elongated square bipyramid is one of the Johnson solids (J15). As the name suggests, it can be constructed by elongating an octahedron by inserting a cube between its congruent halves.
The cubic honeycomb or cubic cellulation is the only proper regular space-filling tessellation in Euclidean 3-space made up of cubic cells. It has 4 cubes around every edge, and 8 cubes around each vertex. Its vertex figure is a regular octahedron. It is a self-dual tessellation with Schläfli symbol {4,3,4}. John Horton Conway called this honeycomb a cubille.
The tetrahedral-octahedral honeycomb, alternated cubic honeycomb is a quasiregular space-filling tessellation in Euclidean 3-space. It is composed of alternating regular octahedra and tetrahedra in a ratio of 1:2.
In geometry, a truncated 24-cell is a uniform 4-polytope formed as the truncation of the regular 24-cell.
The compound of five cubes is one of the five regular polyhedral compounds. It was first described by Edmund Hess in 1876.
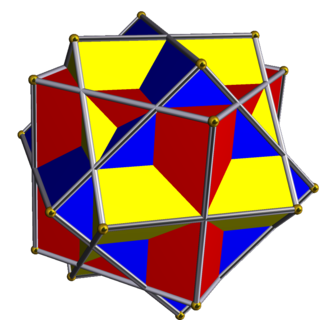
In geometry, the compound of three cubes is a uniform polyhedron compound formed from three cubes arranged with octahedral symmetry. It has been depicted in works by Max Brückner and M.C. Escher.
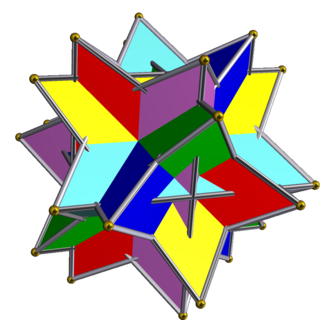
The compound of six tetrahedra is a uniform polyhedron compound. It's composed of a symmetric arrangement of 6 tetrahedra. It can be constructed by inscribing a stella octangula within each cube in the compound of three cubes, or by stellating each octahedron in the compound of three octahedra.
The compound of four octahedra is a uniform polyhedron compound. It's composed of a symmetric arrangement of 4 octahedra, considered as triangular antiprisms. It can be constructed by superimposing four identical octahedra, and then rotating each by 60 degrees about a separate axis.
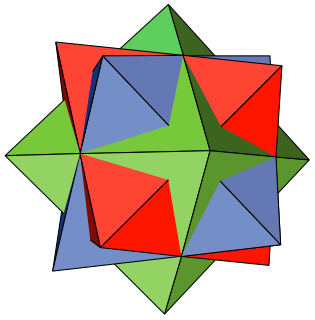
In mathematics, the compound of three octahedra or octahedron 3-compound is a polyhedral compound formed from three regular octahedra, all sharing a common center but rotated with respect to each other. Although appearing earlier in the mathematical literature, it was rediscovered and popularized by M. C. Escher, who used it in the central image of his 1948 woodcut Stars.
The compound of four cubes or Bakos compound is a face-transitive polyhedron compound of four cubes with octahedral symmetry. It is the dual of the compound of four octahedra. Its surface area is 687/77 square lengths of the edge.
A compound of six cubes has two forms. One form is a symmetric arrangement of six cubes, considered as square prisms. It is a special case of the compound of six cubes with rotational freedom.
References
 | This polyhedron-related article is a stub. You can help Wikipedia by expanding it. |