| Compound of two great icosahedra | |
|---|---|
 | |
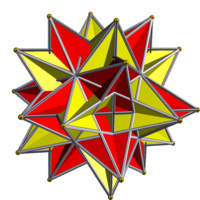| Type | Uniform compound |
| Index | UC52 |
| Polyhedra | 2 great icosahedra |
| Faces | 16+24 triangles |
| Edges | 60 |
| Vertices | 24 |
| Symmetry group | octahedral (Oh) |
| Subgroup restricting to one constituent | pyritohedral (Th) |
In geometry, the compound of two great icosahedra is a uniform polyhedron compound. It is composed of 2 great icosahedra, in the same arrangement as in the compound of 2 icosahedra.
The triangles in this compound decompose into two orbits under action of the symmetry group: 16 of the triangles lie in coplanar pairs in octahedral planes, while the other 24 lie in unique planes.
The great icosahedron, as a uniform retrosnub tetrahedron 
, is similar to these snub-pair compounds: compound of two icosahedra, compound of two snub cubes and compound of two snub dodecahedra.
