
A composite material is a material which is produced from two or more constituent materials. These constituent materials have notably dissimilar chemical or physical properties and are merged to create a material with properties unlike the individual elements. Within the finished structure, the individual elements remain separate and distinct, distinguishing composites from mixtures and solid solutions.
Linear elasticity is a mathematical model of how solid objects deform and become internally stressed due to prescribed loading conditions. It is a simplification of the more general nonlinear theory of elasticity and a branch of continuum mechanics.
In the calculus of variations, a field of mathematical analysis, the functional derivative relates a change in a functional to a change in a function on which the functional depends.

In materials science, work hardening, also known as strain hardening, is the strengthening of a metal or polymer by plastic deformation. Work hardening may be desirable, undesirable, or inconsequential, depending on the context.
Scanning tunneling spectroscopy (STS), an extension of scanning tunneling microscopy (STM), is used to provide information about the density of electrons in a sample as a function of their energy.

The three-point bending flexural test provides values for the modulus of elasticity in bending , flexural stress , flexural strain and the flexural stress–strain response of the material. This test is performed on a universal testing machine with a three-point or four-point bend fixture. The main advantage of a three-point flexural test is the ease of the specimen preparation and testing. However, this method has also some disadvantages: the results of the testing method are sensitive to specimen and loading geometry and strain rate.
In information theory, information dimension is an information measure for random vectors in Euclidean space, based on the normalized entropy of finely quantized versions of the random vectors. This concept was first introduced by Alfréd Rényi in 1959.
Cylindrical multipole moments are the coefficients in a series expansion of a potential that varies logarithmically with the distance to a source, i.e., as . Such potentials arise in the electric potential of long line charges, and the analogous sources for the magnetic potential and gravitational potential.
In statistics, Bayesian multivariate linear regression is a Bayesian approach to multivariate linear regression, i.e. linear regression where the predicted outcome is a vector of correlated random variables rather than a single scalar random variable. A more general treatment of this approach can be found in the article MMSE estimator.

The neutral axis is an axis in the cross section of a beam or shaft along which there are no longitudinal stresses or strains. If the section is symmetric, isotropic and is not curved before a bend occurs, then the neutral axis is at the geometric centroid. All fibers on one side of the neutral axis are in a state of tension, while those on the opposite side are in compression.

In general relativity, a point mass deflects a light ray with impact parameter by an angle approximately equal to
Thermo-mechanical fatigue is the overlay of a cyclical mechanical loading, that leads to fatigue of a material, with a cyclical thermal loading. Thermo-mechanical fatigue is an important point that needs to be considered, when constructing turbine engines or gas turbines.
In solid mechanics, the Johnson–Holmquist damage model is used to model the mechanical behavior of damaged brittle materials, such as ceramics, rocks, and concrete, over a range of strain rates. Such materials usually have high compressive strength but low tensile strength and tend to exhibit progressive damage under load due to the growth of microfractures.
In continuum mechanics, a compatible deformation tensor field in a body is that unique tensor field that is obtained when the body is subjected to a continuous, single-valued, displacement field. Compatibility is the study of the conditions under which such a displacement field can be guaranteed. Compatibility conditions are particular cases of integrability conditions and were first derived for linear elasticity by Barré de Saint-Venant in 1864 and proved rigorously by Beltrami in 1886.
Carbon nanotube springs are springs made of carbon nanotubes (CNTs). They are an alternate form of high density, lightweight, reversible energy storage based on the elastic deformations of CNTs. Many previous studies on the mechanical properties of CNTs have revealed that they possess high stiffness, strength and flexibility. The Young's modulus of CNTs is 1 TPa and they have the ability to sustain reversible tensile strains of 6% and the mechanical springs based on these structures are likely to surpass the current energy storage capabilities of existing steel springs and provide a viable alternative to electrochemical batteries. The obtainable energy density is predicted to be highest under tensile loading, with an energy density in the springs themselves about 2500 times greater than the energy density that can be reached in steel springs, and 10 times greater than the energy density of lithium-ion batteries.
Slip ratio in gas–liquid (two-phase) flow, is defined as the ratio of the velocity of the gas phase to the velocity of the liquid phase.
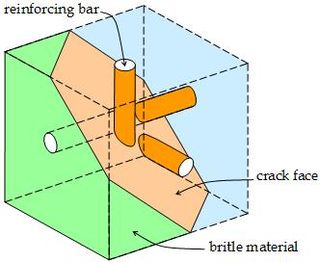
In solid mechanics, a reinforced solid is a brittle material that is reinforced by ductile bars or fibres. A common application is reinforced concrete. When the concrete cracks the tensile force in a crack is not carried any more by the concrete but by the steel reinforcing bars only. The reinforced concrete will continue to carry the load provided that sufficient reinforcement is present. A typical design problem is to find the smallest amount of reinforcement that can carry the stresses on a small cube. This can be formulated as an optimization problem.
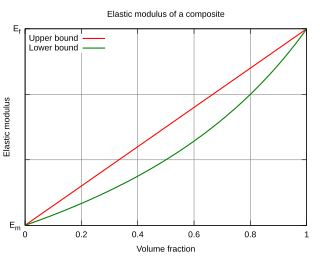
In materials science, a general rule of mixtures is a weighted mean used to predict various properties of a composite material. It provides a theoretical upper- and lower-bound on properties such as the elastic modulus, mass density, ultimate tensile strength, thermal conductivity, and electrical conductivity. In general there are two models, one for axial loading, and one for transverse loading.
Toughening is the improvement of the fracture resistance of a given material. The material's toughness is described by irreversible work accompanying crack propagation. Designing against this crack propagation leads to toughening the material.
Geometrically necessary dislocations are like-signed dislocations needed to accommodate for plastic bending in a crystalline material. They are present when a material's plastic deformation is accompanied by internal plastic strain gradients. They are in contrast to statistically stored dislocations, with statistics of equal positive and negative signs, which arise during plastic flow from multiplication processes like the Frank-Read source.

























