Related Research Articles

In geometry, a polyhedron is a three-dimensional shape with flat polygonal faces, straight edges and sharp corners or vertices.
In geometry, a Platonic solid is a convex, regular polyhedron in three-dimensional Euclidean space. Being a regular polyhedron means that the faces are congruent regular polygons, and the same number of faces meet at each vertex. There are only five such polyhedra:

In geometry, the rhombicuboctahedron, or small rhombicuboctahedron, is a polyhedron with eight triangular, six square, and twelve rectangular faces. There are 24 identical vertices, with one triangle, one square, and two rectangles meeting at each one. If all the rectangles are themselves square, it is an Archimedean solid. The polyhedron has octahedral symmetry, like the cube and octahedron. Its dual is called the deltoidal icositetrahedron or trapezoidal icositetrahedron, although its faces are not really true trapezoids.

In mathematics, topology is concerned with the properties of a geometric object that are preserved under continuous deformations, such as stretching, twisting, crumpling, and bending; that is, without closing holes, opening holes, tearing, gluing, or passing through itself.

In geometry, a tesseract is the four-dimensional analogue of the cube; the tesseract is to the cube as the cube is to the square. Just as the surface of the cube consists of six square faces, the hypersurface of the tesseract consists of eight cubical cells. The tesseract is one of the six convex regular 4-polytopes.

John Willard Milnor is an American mathematician known for his work in differential topology, algebraic K-theory and low-dimensional holomorphic dynamical systems. Milnor is a distinguished professor at Stony Brook University and one of the five mathematicians to have won the Fields Medal, the Wolf Prize, and the Abel Prize.

Squaring the square is the problem of tiling an integral square using only other integral squares. The name was coined in a humorous analogy with squaring the circle. Squaring the square is an easy task unless additional conditions are set. The most studied restriction is that the squaring be perfect, meaning the sizes of the smaller squares are all different. A related problem is squaring the plane, which can be done even with the restriction that each natural number occurs exactly once as a size of a square in the tiling. The order of a squared square is its number of constituent squares.

In mathematics, a ball is the solid figure bounded by a sphere; it is also called a solid sphere. It may be a closed ball or an open ball.

The Alexander horned sphere is a pathological object in topology discovered by J. W. Alexander (1924).

In geometry, a tetrakis hexahedron is a Catalan solid. Its dual is the truncated octahedron, an Archimedean solid.
R. H. Bing was an American mathematician who worked mainly in the areas of geometric topology and continuum theory. His father was named Rupert Henry, but Bing's mother thought that "Rupert Henry" was too British for Texas. She compromised by abbreviating it to R. H. Consequently, R. H. does not stand for a first or middle name.
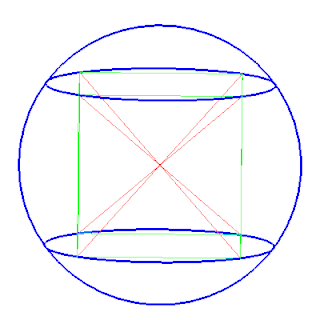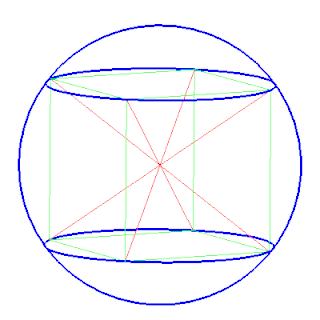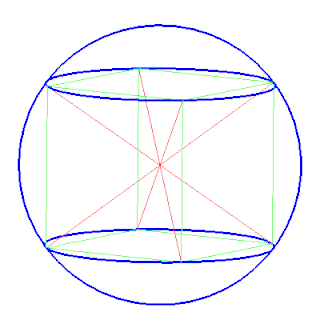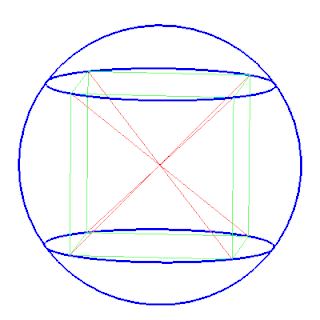
In geometry, a circumscribed sphere of a polyhedron is a sphere that contains the polyhedron and touches each of the polyhedron's vertices. The word circumsphere is sometimes used to mean the same thing, by analogy with the term circumcircle. As in the case of two-dimensional circumscribed circles (circumcircles), the radius of a sphere circumscribed around a polyhedron P is called the circumradius of P, and the center point of this sphere is called the circumcenter of P.

Four-dimensional space (4D) is the mathematical extension of the concept of three-dimensional space (3D). Three-dimensional space is the simplest possible abstraction of the observation that one needs only three numbers, called dimensions, to describe the sizes or locations of objects in the everyday world. For example, the volume of a rectangular box is found by measuring and multiplying its length, width, and height. This concept of ordinary space is called Euclidean space because it corresponds to Euclid's geometry, which was originally abstracted from the spatial experiences of everyday life. The fourth dimension can also refer to relationship between "space and time are interwoven in a 4D fabric that [scientists and mathematicians] call 'space-time'".

In geometry, the midsphere or intersphere of a convex polyhedron is a sphere which is tangent to every edge of the polyhedron. Not every polyhedron has a midsphere, but the uniform polyhedra, including the regular, quasiregular and semiregular polyhedra and their duals all have midspheres. The radius of the midsphere is called the midradius. A polyhedron that has a midsphere is said to be midscribed about this sphere.

A regular dodecahedron or pentagonal dodecahedron is a dodecahedron that is regular, which is composed of 12 regular pentagonal faces, three meeting at each vertex. It is one of the five Platonic solids. It has 12 faces, 20 vertices, 30 edges, and 160 diagonals. It is represented by the Schläfli symbol {5,3}.

The surface-area-to-volume ratio or surface-to-volume ratio is the ratio between surface area and volume of an object or collection of objects.
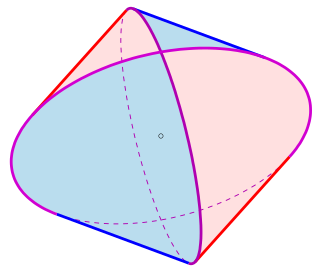
In geometry, a Steinmetz solid is the solid body obtained as the intersection of two or three cylinders of equal radius at right angles. Each of the curves of the intersection of two cylinders is an ellipse.
Kakutani's theorem is a result in geometry named after Shizuo Kakutani. It states that every convex body in 3-dimensional space has a circumscribed cube, i.e. a cube all of whose faces touch the body. The result was further generalized by Yamabe and Yujobô to higher dimensions, and by Floyd to other circumscribed parallelepipeds.
In convex geometry, the Mahler volume of a centrally symmetric convex body is a dimensionless quantity that is associated with the body and is invariant under linear transformations. It is named after German-English mathematician Kurt Mahler. It is known that the shapes with the largest possible Mahler volume are the balls and solid ellipsoids; this is now known as the Blaschke–Santaló inequality. The still-unsolved Mahler conjecture states that the minimum possible Mahler volume is attained by a hypercube.

In three-dimensional hyperbolic geometry, an ideal polyhedron is a convex polyhedron all of whose vertices are ideal points, points "at infinity" rather than interior to three-dimensional hyperbolic space. It can be defined as the convex hull of a finite set of ideal points. An ideal polyhedron has ideal polygons as its faces, meeting along lines of the hyperbolic space.
References
- ↑ Martin, Joseph (1966). "The sum of two crumpled cubes". Michigan Mathematical Journal . 13 (2): 147–151. doi: 10.1307/mmj/1028999538 .

- ↑ Lininger, Lloyd L. (1965). "Some results on crumpled cubes". Transactions of the American Mathematical Society . 118: 534–549. doi: 10.2307/1993977 . ISSN 0002-9947. JSTOR 1993977. MR 0178460.
