In mathematics, a linear map is a mapping between two vector spaces that preserves the operations of vector addition and scalar multiplication. The same names and the same definition are also used for the more general case of modules over a ring; see Module homomorphism.

Linear algebra is the branch of mathematics concerning linear equations such as:
In linear algebra, the rank of a matrix A is the dimension of the vector space generated by its columns. This corresponds to the maximal number of linearly independent columns of A. This, in turn, is identical to the dimension of the vector space spanned by its rows. Rank is thus a measure of the "nondegenerateness" of the system of linear equations and linear transformation encoded by A. There are multiple equivalent definitions of rank. A matrix's rank is one of its most fundamental characteristics.

In Euclidean geometry, an affine transformation, or an affinity, is a geometric transformation that preserves lines and parallelism.

In mathematics, and more specifically in linear algebra, a linear subspace, also known as a vector subspace is a vector space that is a subset of some larger vector space. A linear subspace is usually simply called a subspace when the context serves to distinguish it from other types of subspaces.

In linear algebra, the column space of a matrix A is the span of its column vectors. The column space of a matrix is the image or range of the corresponding matrix transformation.
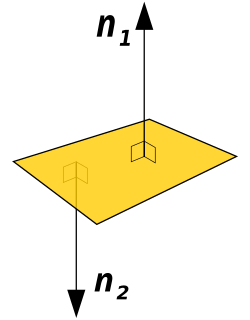
In geometry, a normal is an object such as a line, ray, or vector that is perpendicular to a given object. For example, in two dimensions, the normal line to a curve at a given point is the line perpendicular to the tangent line to the curve at the point. A normal vector may have length one or its length may represent the curvature of the object ; its algebraic sign may indicate sides.
In mathematics, a symplectic vector space is a vector space V over a field F equipped with a symplectic bilinear form.

In linear algebra, a Jordan normal form, also known as a Jordan canonical form or JCF, is an upper triangular matrix of a particular form called a Jordan matrix representing a linear operator on a finite-dimensional vector space with respect to some basis. Such a matrix has each non-zero off-diagonal entry equal to 1, immediately above the main diagonal, and with identical diagonal entries to the left and below them.

In linear algebra and functional analysis, a projection is a linear transformation from a vector space to itself such that . That is, whenever is applied twice to any value, it gives the same result as if it were applied once (idempotent). It leaves its image unchanged. Though abstract, this definition of "projection" formalizes and generalizes the idea of graphical projection. One can also consider the effect of a projection on a geometrical object by examining the effect of the projection on points in the object.
In mathematics, an invariant subspace of a linear mapping T : V → V from some vector space V to itself, is a subspace W of V that is preserved by T; that is, T(W) ⊆ W.
In linear algebra, a coordinate vector is a representation of a vector as an ordered list of numbers that describes the vector in terms of a particular ordered basis. Coordinates are always specified relative to an ordered basis. Bases and their associated coordinate representations let one realize vector spaces and linear transformations concretely as column vectors, row vectors, and matrices; hence, they are useful in calculations.
In linear algebra, a circulant matrix is a square matrix in which each row vector is rotated one element to the right relative to the preceding row vector. It is a particular kind of Toeplitz matrix.
In mathematics, the kernel of a linear map, also known as the null space or nullspace, is the linear subspace of the domain of the map which is mapped to the zero vector. That is, given a linear map L : V → W between two vector spaces V and W, the kernel of L is the vector space of all elements v of V such that L(v) = 0, where 0 denotes the zero vector in W, or more symbolically:
In linear algebra, the Frobenius normal form or rational canonical form of a square matrix A with entries in a field F is a canonical form for matrices obtained by conjugation by invertible matrices over F. The form reflects a minimal decomposition of the vector space into subspaces that are cyclic for A. Since only one normal form can be reached from a given matrix, a matrix B is similar to A if and only if it has the same rational canonical form as A. Since this form can be found without any operations that might change when extending the field F, notably without factoring polynomials, this shows that whether two matrices are similar does not change upon field extensions. The form is named after German mathematician Ferdinand Georg Frobenius.
In linear algebra, a nilpotent matrix is a square matrix N such that

In mathematics, an ordered basis of a vector space of finite dimension n allows representing uniquely any element of the vector space by a coordinate vector, which is a sequence of n scalars called coordinates. If two different bases are considered, the coordinate vector that represents a vector v on one basis is, in general, different from the coordinate vector that represents v on the other basis. A change of basis consists of converting every assertion expressed in terms of coordinates relative to one basis into an assertion expressed in terms of coordinates relative to the other basis.
A symmetric bilinear form on a vector space is a bilinear map from two copies of the vector space to the field of scalars such that the order of the two vectors does not affect the value of the map. In other words, it is a bilinear function that maps every pair of elements of the vector space to the underlying field such that for every and in . They are also referred to more briefly as just symmetric forms when "bilinear" is understood.
In linear algebra, an eigenvector or characteristic vector of a linear transformation is a nonzero vector that changes at most by a scalar factor when that linear transformation is applied to it. The corresponding eigenvalue, often denoted by , is the factor by which the eigenvector is scaled.
In linear algebra, the minimal polynomialμA of an n × n matrix A over a field F is the monic polynomial P over F of least degree such that P(A) = 0. Any other polynomial Q with Q(A) = 0 is a (polynomial) multiple of μA.

































