Visualizations
Each can be visualized as symmetric orthographic projections in Coxeter planes of the D4 Coxeter group, and other subgroups. The B4 coxeter planes are also displayed, while D4 polytopes only have half the symmetry. They can also be shown in perspective projections of Schlegel diagrams, centered on different cells.
| index | Name Coxeter diagram | Coxeter plane projections | Schlegel diagrams | Net | |||
|---|---|---|---|---|---|---|---|
| B4 [8] | D4, B3 [6] | D3, B2 [4] | Cube centered | Tetrahedron centered | |||
| 1 | demitesseract (Same as 16-cell) {3,31,1} | 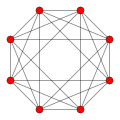 |  |  |  |  | |
| 2 | cantic tesseract (Same as truncated 16-cell) t{3,31,1} |  | 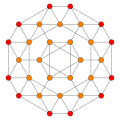 |  | 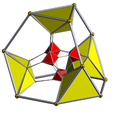 | 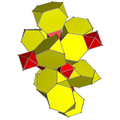 | |
| 3 | runcic tesseract birectified 16-cell (Same as rectified tesseract) 2r{3,31,1} | 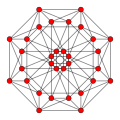 |  |  |  | 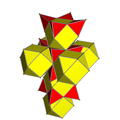 | |
| 4 | runcicantic tesseract bitruncated 16-cell (Same as bitruncated tesseract) 2t{3,31,1} |  | 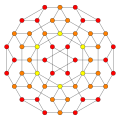 |  | 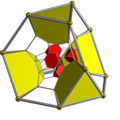 | 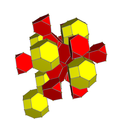 | |
| index | Name Coxeter diagram | Coxeter plane projections | Schlegel diagrams | Parallel 3D | Net | ||||
|---|---|---|---|---|---|---|---|---|---|
| F4 [12] | B4 [8] | D4, B3 [6] | D3, B2 [2] | Cube centered | Tetrahedron centered | D4 [6] | |||
| 5 | rectified 16-cell (Same as 24-cell ) {31,1,1} = r{3,3,4} = {3,4,3} |  | 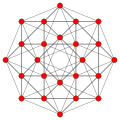 |  | 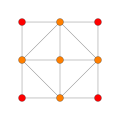 |  | 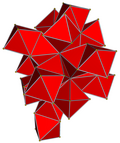 | ||
| 6 | cantellated 16-cell (Same as rectified 24-cell ) r{31,1,1} = rr{3,3,4} = r{3,4,3} |  |  |  |  |  |  | ||
| 7 | cantitruncated 16-cell (Same as truncated 24-cell ) t{31,1,1} = tr{3,31,1} = tr{3,3,4} = t{3,4,3} |  |  |  |  |  |  | ||
| 8 | (Same as snub 24-cell) s{31,1,1} = sr{3,31,1} = sr{3,3,4} = s{3,4,3} |  |  |  |  |  |  | ||