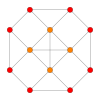
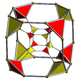
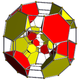
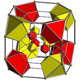
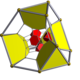
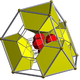
In geometry, a cuboctahedron is a polyhedron with 8 triangular faces and 6 square faces. A cuboctahedron has 12 identical vertices, with 2 triangles and 2 squares meeting at each, and 24 identical edges, each separating a triangle from a square. As such, it is a quasiregular polyhedron, i.e. an Archimedean solid that is not only vertex-transitive but also edge-transitive. It is the only radially equilateral convex polyhedron.

In geometry, a 4-polytope is a four-dimensional polytope. It is a connected and closed figure, composed of lower-dimensional polytopal elements: vertices, edges, faces (polygons), and cells (polyhedra). Each face is shared by exactly two cells.

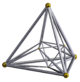
In geometry, the 5-cell is a four-dimensional object bounded by 5 tetrahedral cells. It is also known as a C5, pentachoron, pentatope, pentahedroid, or tetrahedral pyramid. It is the 4-simplex (Coxeter's polytope), the simplest possible convex regular 4-polytope (four-dimensional analogue of a Platonic solid), and is analogous to the tetrahedron in three dimensions and the triangle in two dimensions. The pentachoron is a four dimensional pyramid with a tetrahedral base.

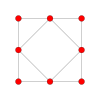
In four-dimensional geometry, a 16-cell is a regular convex 4-polytope. It is one of the six regular convex 4-polytopes first described by the Swiss mathematician Ludwig Schläfli in the mid-19th century. It is also called C16, hexadecachoron, or hexdecahedroid.

In four-dimensional geometry, a runcinated 5-cell is a convex uniform 4-polytope, being a runcination of the regular 5-cell.

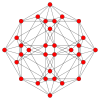
In four-dimensional geometry, a runcinated tesseract is a convex uniform 4-polytope, being a runcination of the regular tesseract.

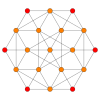
In four-dimensional geometry, a cantellated tesseract is a convex uniform 4-polytope, being a cantellation of the regular tesseract.

The cubic honeycomb or cubic cellulation is the only proper regular space-filling tessellation in Euclidean 3-space, made up of cubic cells. It has 4 cubes around every edge, and 8 cubes around each vertex. Its vertex figure is a regular octahedron. It is a self-dual tessellation with Schläfli symbol {4,3,4}. John Horton Conway calls this honeycomb a cubille.

The order-5 cubic honeycomb is one of four compact regular space-filling tessellations in hyperbolic 3-space. With Schläfli symbol {4,3,5}, it has five cubes {4,3} around each edge, and 20 cubes around each vertex. It is dual with the order-4 dodecahedral honeycomb.
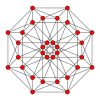
In geometry, a truncated tesseract is a uniform 4-polytope formed as the truncation of the regular tesseract.

In geometry, the rectified 24-cell or rectified icositetrachoron is a uniform 4-dimensional polytope, which is bounded by 48 cells: 24 cubes, and 24 cuboctahedra. It can be obtained by rectification of the 24-cell, reducing its octahedral cells to cubes and cuboctahedra.

In four-dimensional geometry, a cantellated 24-cell is a convex uniform 4-polytope, being a cantellation of the regular 24-cell.
In five-dimensional geometry, a 5-cube is a name for a five-dimensional hypercube with 32 vertices, 80 edges, 80 square faces, 40 cubic cells, and 10 tesseract 4-faces.
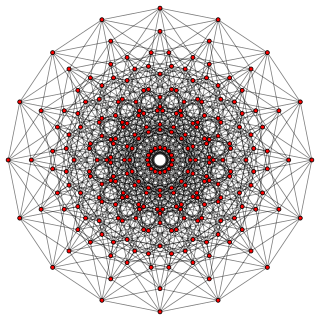
In geometry, an 8-cube is an eight-dimensional hypercube (8-cube). It has 256 vertices, 1024 edges, 1792 square faces, 1792 cubic cells, 1120 tesseract 4-faces, 448 5-cube 5-faces, 112 6-cube 6-faces, and 16 7-cube 7-faces.

In geometry, a 9-cube is a nine-dimensional hypercube with 512 vertices, 2304 edges, 4608 square faces, 5376 cubic cells, 4032 tesseract 4-faces, 2016 5-cube 5-faces, 672 6-cube 6-faces, 144 7-cube 7-faces, and 18 8-cube 8-faces.

In geometry, a 10-cube is a ten-dimensional hypercube. It has 1024 vertices, 5120 edges, 11520 square faces, 15360 cubic cells, 13440 tesseract 4-faces, 8064 5-cube 5-faces, 3360 6-cube 6-faces, 960 7-cube 7-faces, 180 8-cube 8-faces, and 20 9-cube 9-faces.
In seven-dimensional geometry, a rectified 7-orthoplex is a convex uniform 7-polytope, being a rectification of the regular 7-orthoplex.

In six-dimensional geometry, a runcic 5-cube or is a convex uniform 5-polytope. There are 2 runcic forms for the 5-cube. Runcic 5-cubes have half the vertices of runcinated 5-cubes.


![]()
![]()
![]()
![]()
![]()
![]()
![]()