Uniform 5-polytope

Graphs of regular and uniform 5-polytopes.

5-simplex				Rectified 5-simplex				Truncated 5-simplex
Cantellated 5-simplex				Runcinated 5-simplex				Stericated 5-simplex
5-orthoplex				Truncated 5-orthoplex				Rectified 5-orthoplex
Cantellated 5-orthoplex						Runcinated 5-orthoplex
Cantellated 5-cube				Runcinated 5-cube				Stericated 5-cube
5-cube				Truncated 5-cube				Rectified 5-cube
5-demicube						Truncated 5-demicube
Cantellated 5-demicube						Runcinated 5-demicube

In geometry, a uniform 5-polytope is a five-dimensional uniform polytope. By definition, a uniform 5-polytope is vertex-transitive and constructed from uniform 4-polytope facets.

The complete set of convex uniform 5-polytopes has not been determined, but many can be made as Wythoff constructions from a small set of symmetry groups. These construction operations are represented by the permutations of rings of the Coxeter diagrams.

History of discovery

• Regular polytopes : (convex faces)
  • 1852: Ludwig Schläfli proved in his manuscript Theorie der vielfachen Kontinuität that there are exactly 3 regular polytopes in 5 or more dimensions.
• Convex semiregular polytopes : (Various definitions before Coxeter's uniform category)
  • 1900: Thorold Gosset enumerated the list of nonprismatic semiregular convex polytopes with regular facets (convex regular 4-polytopes) in his publication On the Regular and Semi-Regular Figures in Space of n Dimensions. ^[1]
• Convex uniform polytopes:
  • 1940-1988: The search was expanded systematically by H.S.M. Coxeter in his publication Regular and Semi-Regular Polytopes I, II, and III.
  • 1966: Norman W. Johnson completed his Ph.D. Dissertation under Coxeter, The Theory of Uniform Polytopes and Honeycombs, University of Toronto
• Non-convex uniform polytopes:
  • 1966: Johnson describes two non-convex uniform antiprisms in 5-space in his dissertation. ^[2]
  • 2000-2024: Jonathan Bowers and other researchers search for other non-convex uniform 5-polytopes, ^[3] with a current count of 1298 known uniform 5-polytopes outside infinite families (convex and non-convex), excluding the prisms of the uniform 4-polytopes. The list is not proven complete. ^{[4] [5]}

Regular 5-polytopes

Main article: List of regular polytopes § Five Dimensions

Regular 5-polytopes can be represented by the Schläfli symbol {p,q,r,s}, with s {p,q,r} 4-polytope facets around each face. There are exactly three such regular polytopes, all convex:

• {3,3,3,3} - 5-simplex
• {4,3,3,3} - 5-cube
• {3,3,3,4} - 5-orthoplex

There are no nonconvex regular polytopes in 5 dimensions or above.

Convex uniform 5-polytopes

Unsolved problem in mathematics:

What is the complete set of convex uniform 5-polytopes? ^[6]

(more unsolved problems in mathematics)

There are 104 known convex uniform 5-polytopes, plus a number of infinite families of duoprism prisms, and polygon-polyhedron duoprisms. All except the grand antiprism prism are based on Wythoff constructions, reflection symmetry generated with Coxeter groups.^{[ citation needed ]}

Symmetry of uniform 5-polytopes in four dimensions

The 5-simplex is the regular form in the A₅ family. The 5-cube and 5-orthoplex are the regular forms in the B₅ family. The bifurcating graph of the D₅ family contains the 5-orthoplex, as well as a 5-demicube which is an alternated 5-cube.

Each reflective uniform 5-polytope can be constructed in one or more reflective point group in 5 dimensions by a Wythoff construction, represented by rings around permutations of nodes in a Coxeter diagram. Mirror hyperplanes can be grouped, as seen by colored nodes, separated by even-branches. Symmetry groups of the form [a,b,b,a], have an extended symmetry, [[a,b,b,a]], like [3,3,3,3], doubling the symmetry order. Uniform polytopes in these group with symmetric rings contain this extended symmetry.

If all mirrors of a given color are unringed (inactive) in a given uniform polytope, it will have a lower symmetry construction by removing all of the inactive mirrors. If all the nodes of a given color are ringed (active), an alternation operation can generate a new 5-polytope with chiral symmetry, shown as "empty" circled nodes", but the geometry is not generally adjustable to create uniform solutions.

Coxeter diagram correspondences between families and higher symmetry within diagrams. Nodes of the same color in each row represent identical mirrors. Black nodes are not active in the correspondence.

Fundamental families ^[7]

Group symbol	Order	Coxeter graph		Bracket notation	Commutator subgroup	Coxeter number (h)	Reflections m=5/2 h [8]
A5	720			[3,3,3,3]	[3,3,3,3]+	6		15
D5	1920			[3,3,31,1]	[3,3,31,1]+	8		20
B5	3840			[4,3,3,3]		10	5	20

Uniform prisms

There are 5 finite categorical uniform prismatic families of polytopes based on the nonprismatic uniform 4-polytopes. There is one infinite family of 5-polytopes based on prisms of the uniform duoprisms {p}×{q}×{ }.

Coxeter group	Order	Coxeter diagram		Coxeter notation	Commutator subgroup	Reflections
A4A1	120			[3,3,3,2] = [3,3,3]×[ ]	[3,3,3]+			10		1
D4A1	384			[31,1,1,2] = [31,1,1]×[ ]	[31,1,1]+			12		1
B4A1	768			[4,3,3,2] = [4,3,3]×[ ]			4	12		1
F4A1	2304			[3,4,3,2] = [3,4,3]×[ ]	[3+,4,3+]		12	12		1
H4A1	28800			[5,3,3,2] = [3,4,3]×[ ]	[5,3,3]+			60		1
Duoprismatic prisms (use 2p and 2q for evens)
I2(p)I2(q)A1	8pq			[p,2,q,2] = [p]×[q]×[ ]	[p+,2,q+]		p	q		1
I2(2p)I2(q)A1	16pq			[2p,2,q,2] = [2p]×[q]×[ ]		p	p	q		1
I2(2p)I2(2q)A1	32pq			[2p,2,2q,2] = [2p]×[2q]×[ ]		p	p	q	q	1

Uniform duoprisms

There are 3 categorical uniform duoprismatic families of polytopes based on Cartesian products of the uniform polyhedra and regular polygons: {q,r}×{p}.

Coxeter group	Order	Coxeter diagram		Coxeter notation	Commutator subgroup	Reflections
Prismatic groups (use 2p for even)
A3I2(p)	48p			[3,3,2,p] = [3,3]×[p]	[(3,3)+,2,p+]		6	p
A3I2(2p)	96p			[3,3,2,2p] = [3,3]×[2p]			6	p	p
B3I2(p)	96p			[4,3,2,p] = [4,3]×[p]		3	6	p
B3I2(2p)	192p			[4,3,2,2p] = [4,3]×[2p]		3	6	p	p
H3I2(p)	240p			[5,3,2,p] = [5,3]×[p]	[(5,3)+,2,p+]		15	p
H3I2(2p)	480p			[5,3,2,2p] = [5,3]×[2p]			15	p	p

Enumerating the convex uniform 5-polytopes

• Simplex family: A₅ [3⁴]
  • 19 uniform 5-polytopes
• Hypercube/Orthoplex family: B₅ [4,3³]
  • 31 uniform 5-polytopes
• Demihypercube D₅/E₅ family: [3^2,1,1]
  • 23 uniform 5-polytopes (8 unique)
• Polychoral prisms:
  • 56 uniform 5-polytope (45 unique) constructions based on prismatic families: [3,3,3]×[ ], [4,3,3]×[ ], [5,3,3]×[ ], [3^1,1,1]×[ ].
  • One non-Wythoffian - The grand antiprism prism is the only known non-Wythoffian convex uniform 5-polytope, constructed from two grand antiprisms connected by polyhedral prisms.

That brings the tally to: 19+31+8+45+1=104

In addition there are:

• Infinitely many uniform 5-polytope constructions based on duoprism prismatic families: [p]×[q]×[ ].
• Infinitely many uniform 5-polytope constructions based on duoprismatic families: [3,3]×[p], [4,3]×[p], [5,3]×[p].

The A₅ family

Further information: A5 polytope

There are 19 forms based on all permutations of the Coxeter diagrams with one or more rings. (16+4-1 cases)

They are named by Norman Johnson from the Wythoff construction operations upon regular 5-simplex (hexateron).

The A₅ family has symmetry of order 720 (6 factorial). 7 of the 19 figures, with symmetrically ringed Coxeter diagrams have doubled symmetry, order 1440.

The coordinates of uniform 5-polytopes with 5-simplex symmetry can be generated as permutations of simple integers in 6-space, all in hyperplanes with normal vector (1,1,1,1,1,1).

#	Base point	Johnson naming system Bowers name and (acronym) Coxeter diagram	k-face element counts					Vertex figure	Facet counts by location: [3,3,3,3]
			4	3	2	1	0		[3,3,3] (6)	[3,3,2] (15)	[3,2,3] (20)	[2,3,3] (15)	[3,3,3] (6)	Alt
1	(0,0,0,0,0,1) or (0,1,1,1,1,1)	5-simplex hexateron (hix)	6	15	20	15	6	{3,3,3}	{3,3,3}	-	-	-	-
2	(0,0,0,0,1,1) or (0,0,1,1,1,1)	Rectified 5-simplex rectified hexateron (rix)	12	45	80	60	15	t{3,3}×{ }	r{3,3,3}	-	-	-	{3,3,3}
3	(0,0,0,0,1,2) or (0,1,2,2,2,2)	Truncated 5-simplex truncated hexateron (tix)	12	45	80	75	30	Tetrah.pyr	t{3,3,3}	-	-	-	{3,3,3}
4	(0,0,0,1,1,2) or (0,1,1,2,2,2)	Cantellated 5-simplex small rhombated hexateron (sarx)	27	135	290	240	60	prism-wedge	rr{3,3,3}	-	-	{ }×{3,3}	r{3,3,3}
5	(0,0,0,1,2,2) or (0,0,1,2,2,2)	Bitruncated 5-simplex bitruncated hexateron (bittix)	12	60	140	150	60		2t{3,3,3}	-	-	-	t{3,3,3}
6	(0,0,0,1,2,3) or (0,1,2,3,3,3)	Cantitruncated 5-simplex great rhombated hexateron (garx)	27	135	290	300	120		tr{3,3,3}	-	-	{ }×{3,3}	t{3,3,3}
7	(0,0,1,1,1,2) or (0,1,1,1,2,2)	Runcinated 5-simplex small prismated hexateron (spix)	47	255	420	270	60		t0,3{3,3,3}	-	{3}×{3}	{ }×r{3,3}	r{3,3,3}
8	(0,0,1,1,2,3) or (0,1,2,2,3,3)	Runcitruncated 5-simplex prismatotruncated hexateron (pattix)	47	315	720	630	180		t0,1,3{3,3,3}	-	{6}×{3}	{ }×r{3,3}	rr{3,3,3}
9	(0,0,1,2,2,3) or (0,1,1,2,3,3)	Runcicantellated 5-simplex prismatorhombated hexateron (pirx)	47	255	570	540	180		t0,1,3{3,3,3}	-	{3}×{3}	{ }×t{3,3}	2t{3,3,3}
10	(0,0,1,2,3,4) or (0,1,2,3,4,4)	Runcicantitruncated 5-simplex great prismated hexateron (gippix)	47	315	810	900	360	Irr.5-cell	t0,1,2,3{3,3,3}	-	{3}×{6}	{ }×t{3,3}	tr{3,3,3}
11	(0,1,1,1,2,3) or (0,1,2,2,2,3)	Steritruncated 5-simplex celliprismated hexateron (cappix)	62	330	570	420	120		t{3,3,3}	{ }×t{3,3}	{3}×{6}	{ }×{3,3}	t0,3{3,3,3}
12	(0,1,1,2,3,4) or (0,1,2,3,3,4)	Stericantitruncated 5-simplex celligreatorhombated hexateron (cograx)	62	480	1140	1080	360		tr{3,3,3}	{ }×tr{3,3}	{3}×{6}	{ }×rr{3,3}	t0,1,3{3,3,3}
13	(0,0,0,1,1,1)	Birectified 5-simplex dodecateron (dot)	12	60	120	90	20	{3}×{3}	r{3,3,3}	-	-	-	r{3,3,3}
14	(0,0,1,1,2,2)	Bicantellated 5-simplex small birhombated dodecateron (sibrid)	32	180	420	360	90		rr{3,3,3}	-	{3}×{3}	-	rr{3,3,3}
15	(0,0,1,2,3,3)	Bicantitruncated 5-simplex great birhombated dodecateron (gibrid)	32	180	420	450	180		tr{3,3,3}	-	{3}×{3}	-	tr{3,3,3}
16	(0,1,1,1,1,2)	Stericated 5-simplex small cellated dodecateron (scad)	62	180	210	120	30	Irr.16-cell	{3,3,3}	{ }×{3,3}	{3}×{3}	{ }×{3,3}	{3,3,3}
17	(0,1,1,2,2,3)	Stericantellated 5-simplex small cellirhombated dodecateron (card)	62	420	900	720	180		rr{3,3,3}	{ }×rr{3,3}	{3}×{3}	{ }×rr{3,3}	rr{3,3,3}
18	(0,1,2,2,3,4)	Steriruncitruncated 5-simplex celliprismatotruncated dodecateron (captid)	62	450	1110	1080	360		t0,1,3{3,3,3}	{ }×t{3,3}	{6}×{6}	{ }×t{3,3}	t0,1,3{3,3,3}
19	(0,1,2,3,4,5)	Omnitruncated 5-simplex great cellated dodecateron (gocad)	62	540	1560	1800	720	Irr. {3,3,3}	t0,1,2,3{3,3,3}	{ }×tr{3,3}	{6}×{6}	{ }×tr{3,3}	t0,1,2,3{3,3,3}
Nonuniform		Omnisnub 5-simplex snub dodecateron (snod) snub hexateron (snix)	422	2340	4080	2520	360		ht0,1,2,3{3,3,3}	ht0,1,2,3{3,3,2}	ht0,1,2,3{3,2,3}	ht0,1,2,3{3,3,2}	ht0,1,2,3{3,3,3}	(360) Irr. {3,3,3}

The B₅ family

Further information: B5 polytope

The B₅ family has symmetry of order 3840 (5!×2⁵).

This family has 2⁵−1=31 Wythoffian uniform polytopes generated by marking one or more nodes of the Coxeter diagram. Also added are 8 uniform polytopes generated as alternations with half the symmetry, which form a complete duplicate of the D₅ family as ... = ..... (There are more alternations that are not listed because they produce only repetitions, as ... = .... and ... = .... These would give a complete duplication of the uniform 5-polytopes numbered 20 through 34 with symmetry broken in half.)

For simplicity it is divided into two subgroups, each with 12 forms, and 7 "middle" forms which equally belong in both.

The 5-cube family of 5-polytopes are given by the convex hulls of the base points listed in the following table, with all permutations of coordinates and sign taken. Each base point generates a distinct uniform 5-polytope. All coordinates correspond with uniform 5-polytopes of edge length 2.

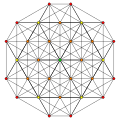
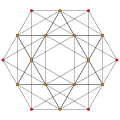
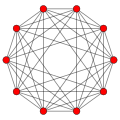
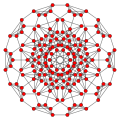
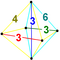
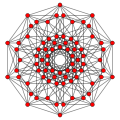
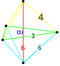
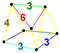
#	Base point	Name Coxeter diagram	Element counts					Vertex figure	Facet counts by location: [4,3,3,3]
			4	3	2	1	0		[4,3,3] (10)	[4,3,2] (40)	[4,2,3] (80)	[2,3,3] (80)	[3,3,3] (32)	Alt
20	(0,0,0,0,1)√2	5-orthoplex triacontaditeron (tac)	32	80	80	40	10	{3,3,4}	-	-	-	-	{3,3,3}
21	(0,0,0,1,1)√2	Rectified 5-orthoplex rectified triacontaditeron (rat)	42	240	400	240	40	{ }×{3,4}	{3,3,4}	-	-	-	r{3,3,3}
22	(0,0,0,1,2)√2	Truncated 5-orthoplex truncated triacontaditeron (tot)	42	240	400	280	80	(Octah.pyr)	{3,3,4}	-	-	-	t{3,3,3}
23	(0,0,1,1,1)√2	Birectified 5-cube penteractitriacontaditeron (nit) (Birectified 5-orthoplex)	42	280	640	480	80	{4}×{3}	r{3,3,4}	-	-	-	r{3,3,3}
24	(0,0,1,1,2)√2	Cantellated 5-orthoplex small rhombated triacontaditeron (sart)	82	640	1520	1200	240	Prism-wedge	r{3,3,4}	{ }×{3,4}	-	-	rr{3,3,3}
25	(0,0,1,2,2)√2	Bitruncated 5-orthoplex bitruncated triacontaditeron (bittit)	42	280	720	720	240		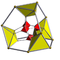t{3,3,4}	-	-	-	2t{3,3,3}
26	(0,0,1,2,3)√2	Cantitruncated 5-orthoplex great rhombated triacontaditeron (gart)	82	640	1520	1440	480		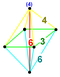t{3,3,4}	{ }×{3,4}	-	-	t0,1,3{3,3,3}
27	(0,1,1,1,1)√2	Rectified 5-cube rectified penteract (rin)	42	200	400	320	80	{3,3}×{ }	r{4,3,3}	-	-	-	{3,3,3}
28	(0,1,1,1,2)√2	Runcinated 5-orthoplex small prismated triacontaditeron (spat)	162	1200	2160	1440	320		r{4,3,3}	{ }×r{3,4}	{3}×{4}		t0,3{3,3,3}
29	(0,1,1,2,2)√2	Bicantellated 5-cube small birhombated penteractitriacontaditeron (sibrant) (Bicantellated 5-orthoplex)	122	840	2160	1920	480		rr{3,3,4}	-	{4}×{3}	-	rr{3,3,3}
30	(0,1,1,2,3)√2	Runcitruncated 5-orthoplex prismatotruncated triacontaditeron (pattit)	162	1440	3680	3360	960		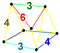rr{3,3,4}	{ }×r{3,4}	{6}×{4}	-	t0,1,3{3,3,3}
31	(0,1,2,2,2)√2	Bitruncated 5-cube bitruncated penteract (bittin)	42	280	720	800	320		2t{4,3,3}	-	-	-	t{3,3,3}
32	(0,1,2,2,3)√2	Runcicantellated 5-orthoplex prismatorhombated triacontaditeron (pirt)	162	1200	2960	2880	960		2t{4,3,3}	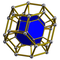{ }×t{3,4}	{3}×{4}	-	t0,1,3{3,3,3}
33	(0,1,2,3,3)√2	Bicantitruncated 5-cube great birhombated triacontaditeron (gibrant) (Bicantitruncated 5-orthoplex)	122	840	2160	2400	960		tr{3,3,4}	-	{4}×{3}	-	rr{3,3,3}
34	(0,1,2,3,4)√2	Runcicantitruncated 5-orthoplex great prismated triacontaditeron (gippit)	162	1440	4160	4800	1920		tr{3,3,4}	{ }×t{3,4}	{6}×{4}	-	t0,1,2,3{3,3,3}
35	(1,1,1,1,1)	5-cube penteract (pent)	10	40	80	80	32	{3,3,3}	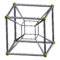{4,3,3}	-	-	-	-
36	(1,1,1,1,1) + (0,0,0,0,1)√2	Stericated 5-cube small cellated penteractitriacontaditeron (scant) (Stericated 5-orthoplex)	242	800	1040	640	160	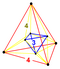Tetr.antiprm	{4,3,3}	{4,3}×{ }	{4}×{3}	{ }×{3,3}	{3,3,3}
37	(1,1,1,1,1) + (0,0,0,1,1)√2	Runcinated 5-cube small prismated penteract (span)	202	1240	2160	1440	320		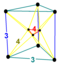t0,3{4,3,3}	-	{4}×{3}	{ }×r{3,3}	r{3,3,3}
38	(1,1,1,1,1) + (0,0,0,1,2)√2	Steritruncated 5-orthoplex celliprismated triacontaditeron (cappin)	242	1520	2880	2240	640		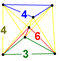t0,3{4,3,3}	{4,3}×{ }	{6}×{4}	{ }×t{3,3}	t{3,3,3}
39	(1,1,1,1,1) + (0,0,1,1,1)√2	Cantellated 5-cube small rhombated penteract (sirn)	122	680	1520	1280	320	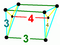Prism-wedge	rr{4,3,3}	-	-	{ }×{3,3}	r{3,3,3}
40	(1,1,1,1,1) + (0,0,1,1,2)√2	Stericantellated 5-cube cellirhombated penteractitriacontaditeron (carnit) (Stericantellated 5-orthoplex)	242	2080	4720	3840	960		rr{4,3,3}	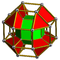rr{4,3}×{ }	{4}×{3}	{ }×rr{3,3}	rr{3,3,3}
41	(1,1,1,1,1) + (0,0,1,2,2)√2	Runcicantellated 5-cube prismatorhombated penteract (prin)	202	1240	2960	2880	960		t0,2,3{4,3,3}	-	{4}×{3}	{ }×t{3,3}	2t{3,3,3}
42	(1,1,1,1,1) + (0,0,1,2,3)√2	Stericantitruncated 5-orthoplex celligreatorhombated triacontaditeron (cogart)	242	2320	5920	5760	1920		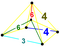t0,2,3{4,3,3}	rr{4,3}×{ }	{6}×{4}	{ }×tr{3,3}	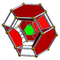tr{3,3,3}
43	(1,1,1,1,1) + (0,1,1,1,1)√2	Truncated 5-cube truncated penteract (tan)	42	200	400	400	160	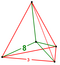Tetrah.pyr	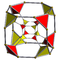t{4,3,3}	-	-	-	{3,3,3}
44	(1,1,1,1,1) + (0,1,1,1,2)√2	Steritruncated 5-cube celliprismated triacontaditeron (capt)	242	1600	2960	2240	640		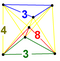t{4,3,3}	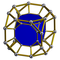t{4,3}×{ }	{8}×{3}	{ }×{3,3}	t0,3{3,3,3}
45	(1,1,1,1,1) + (0,1,1,2,2)√2	Runcitruncated 5-cube prismatotruncated penteract (pattin)	202	1560	3760	3360	960		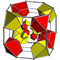t0,1,3{4,3,3}	-	{8}×{3}	{ }×r{3,3}	rr{3,3,3}
46	(1,1,1,1,1) + (0,1,1,2,3)√2	Steriruncitruncated 5-cube celliprismatotruncated penteractitriacontaditeron (captint) (Steriruncitruncated 5-orthoplex)	242	2160	5760	5760	1920		t0,1,3{4,3,3}	t{4,3}×{ }	{8}×{6}	{ }×t{3,3}	t0,1,3{3,3,3}
47	(1,1,1,1,1) + (0,1,2,2,2)√2	Cantitruncated 5-cube great rhombated penteract (girn)	122	680	1520	1600	640		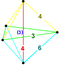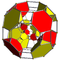tr{4,3,3}	-	-	{ }×{3,3}	t{3,3,3}
48	(1,1,1,1,1) + (0,1,2,2,3)√2	Stericantitruncated 5-cube celligreatorhombated penteract (cogrin)	242	2400	6000	5760	1920		tr{4,3,3}	tr{4,3}×{ }	{8}×{3}	{ }×rr{3,3}	t0,1,3{3,3,3}
49	(1,1,1,1,1) + (0,1,2,3,3)√2	Runcicantitruncated 5-cube great prismated penteract (gippin)	202	1560	4240	4800	1920		t0,1,2,3{4,3,3}	-	{8}×{3}	{ }×t{3,3}	tr{3,3,3}
50	(1,1,1,1,1) + (0,1,2,3,4)√2	Omnitruncated 5-cube great cellated penteractitriacontaditeron (gacnet) (omnitruncated 5-orthoplex)	242	2640	8160	9600	3840	Irr. {3,3,3}	tr{4,3}×{ }	tr{4,3}×{ }	{8}×{6}	{ }×tr{3,3}	t0,1,2,3{3,3,3}
51		5-demicube hemipenteract (hin) =	26	120	160	80	16	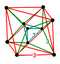r{3,3,3}	h{4,3,3}	-	-	-	-	(16) {3,3,3}
52		Cantic 5-cube Truncated hemipenteract (thin) =	42	280	640	560	160		h2{4,3,3}	-	-	-	(16) r{3,3,3}	(16) t{3,3,3}
53		Runcic 5-cube Small rhombated hemipenteract (sirhin) =	42	360	880	720	160		h3{4,3,3}	-	-	-	(16) r{3,3,3}	(16) rr{3,3,3}
54		Steric 5-cube Small prismated hemipenteract (siphin) =	82	480	720	400	80		h{4,3,3}	h{4,3}×{}	-	-	(16) {3,3,3}	(16) t0,3{3,3,3}
55		Runcicantic 5-cube Great rhombated hemipenteract (girhin) =	42	360	1040	1200	480		h2,3{4,3,3}	-	-	-	(16) 2t{3,3,3}	(16) tr{3,3,3}
56		Stericantic 5-cube Prismatotruncated hemipenteract (pithin) =	82	720	1840	1680	480		h2{4,3,3}	h2{4,3}×{}	-	-	(16) rr{3,3,3}	(16) t0,1,3{3,3,3}
57		Steriruncic 5-cube Prismatorhombated hemipenteract (pirhin) =	82	560	1280	1120	320		h3{4,3,3}	h{4,3}×{}	-	-	(16) t{3,3,3}	(16) t0,1,3{3,3,3}
58		Steriruncicantic 5-cube Great prismated hemipenteract (giphin) =	82	720	2080	2400	960		h2,3{4,3,3}	h2{4,3}×{}	-	-	(16) tr{3,3,3}	(16) t0,1,2,3{3,3,3}
Nonuniform		Alternated runcicantitruncated 5-orthoplex Snub prismatotriacontaditeron (snippit) Snub hemipenteract (snahin) =	1122	6240	10880	6720	960		sr{3,3,4}	sr{2,3,4}	sr{3,2,4}	-	ht0,1,2,3{3,3,3}	(960) Irr. {3,3,3}
Nonuniform		Edge-snub 5-orthoplex Pyritosnub penteract (pysnan)	1202	7920	15360	10560	1920		sr3{3,3,4}	sr3{2,3,4}	sr3{3,2,4}	s{3,3}×{ }	ht0,1,2,3{3,3,3}	(960) Irr. {3,3}×{ }
Nonuniform		Snub 5-cube Snub penteract (snan)	2162	12240	21600	13440	960		ht0,1,2,3{3,3,4}	ht0,1,2,3{2,3,4}	ht0,1,2,3{3,2,4}	ht0,1,2,3{3,3,2}	ht0,1,2,3{3,3,3}	(1920) Irr. {3,3,3}

The D₅ family

Further information: D5 polytope

The D₅ family has symmetry of order 1920 (5! x 2⁴).

This family has 23 Wythoffian uniform polytopes, from 3×8-1 permutations of the D₅ Coxeter diagram with one or more rings. 15 (2×8-1) are repeated from the B₅ family and 8 are unique to this family, though even those 8 duplicate the alternations from the B₅ family.

In the 15 repeats, both of the nodes terminating the length-1 branches are ringed, so the two kinds of element are identical and the symmetry doubles: the relations are ... = .... and ... = ..., creating a complete duplication of the uniform 5-polytopes 20 through 34 above. The 8 new forms have one such node ringed and one not, with the relation ... = ... duplicating uniform 5-polytopes 51 through 58 above.

#	Coxeter diagram Schläfli symbol symbols Johnson and Bowers names	Element counts					Vertex figure	Facets by location: [31,2,1]
		4	3	2	1	0		[3,3,3] (16)	[31,1,1] (10)	[3,3]×[ ] (40)	[ ]×[3]×[ ] (80)	[3,3,3] (16)	Alt
[51]	= h{4,3,3,3}, 5-demicube Hemipenteract (hin)	26	120	160	80	16	r{3,3,3}	{3,3,3}	h{4,3,3}	-	-	-
[52]	= h2{4,3,3,3}, cantic 5-cube Truncated hemipenteract (thin)	42	280	640	560	160		t{3,3,3}	h2{4,3,3}	-	-	r{3,3,3}
[53]	= h3{4,3,3,3}, runcic 5-cube Small rhombated hemipenteract (sirhin)	42	360	880	720	160		rr{3,3,3}	h3{4,3,3}	-	-	r{3,3,3}
[54]	= h4{4,3,3,3}, steric 5-cube Small prismated hemipenteract (siphin)	82	480	720	400	80		t0,3{3,3,3}	h{4,3,3}	h{4,3}×{}	-	{3,3,3}
[55]	= h2,3{4,3,3,3}, runcicantic 5-cube Great rhombated hemipenteract (girhin)	42	360	1040	1200	480		2t{3,3,3}	h2,3{4,3,3}	-	-	tr{3,3,3}
[56]	= h2,4{4,3,3,3}, stericantic 5-cube Prismatotruncated hemipenteract (pithin)	82	720	1840	1680	480		t0,1,3{3,3,3}	h2{4,3,3}	h2{4,3}×{}	-	rr{3,3,3}
[57]	= h3,4{4,3,3,3}, steriruncic 5-cube Prismatorhombated hemipenteract (pirhin)	82	560	1280	1120	320		t0,1,3{3,3,3}	h3{4,3,3}	h{4,3}×{}	-	t{3,3,3}
[58]	= h2,3,4{4,3,3,3}, steriruncicantic 5-cube Great prismated hemipenteract (giphin)	82	720	2080	2400	960		t0,1,2,3{3,3,3}	h2,3{4,3,3}	h2{4,3}×{}	-	tr{3,3,3}
Nonuniform	= ht0,1,2,3{3,3,3,4}, alternated runcicantitruncated 5-orthoplex Snub hemipenteract (snahin)	1122	6240	10880	6720	960		ht0,1,2,3{3,3,3}	sr{3,3,4}	sr{2,3,4}	sr{3,2,4}	ht0,1,2,3{3,3,3}	(960) Irr. {3,3,3}

Uniform prismatic forms

There are 5 finite categorical uniform prismatic families of polytopes based on the nonprismatic uniform 4-polytopes. For simplicity, most alternations are not shown.

A₄ × A₁

This prismatic family has 9 forms:

The A₁ x A₄ family has symmetry of order 240 (2*5!).

#	Coxeter diagram and Schläfli symbols Name	Element counts
		Facets	Cells	Faces	Edges	Vertices
59	= {3,3,3}×{ } 5-cell prism (penp)	7	20	30	25	10
60	= r{3,3,3}×{ } Rectified 5-cell prism (rappip)	12	50	90	70	20
61	= t{3,3,3}×{ } Truncated 5-cell prism (tippip)	12	50	100	100	40
62	= rr{3,3,3}×{ } Cantellated 5-cell prism (srippip)	22	120	250	210	60
63	= t0,3{3,3,3}×{ } Runcinated 5-cell prism (spiddip)	32	130	200	140	40
64	= 2t{3,3,3}×{ } Bitruncated 5-cell prism (decap)	12	60	140	150	60
65	= tr{3,3,3}×{ } Cantitruncated 5-cell prism (grippip)	22	120	280	300	120
66	= t0,1,3{3,3,3}×{ } Runcitruncated 5-cell prism (prippip)	32	180	390	360	120
67	= t0,1,2,3{3,3,3}×{ } Omnitruncated 5-cell prism (gippiddip)	32	210	540	600	240

B₄ × A₁

This prismatic family has 16 forms. (Three are shared with [3,4,3]×[ ] family)

The A₁×B₄ family has symmetry of order 768 (2⁵4!).

The last three snubs can be realised with equal-length edges, but turn out nonuniform anyway because some of their 4-faces are not uniform 4-polytopes.

#	Coxeter diagram and Schläfli symbols Name	Element counts
		Facets	Cells	Faces	Edges	Vertices
[16]	= {4,3,3}×{ } Tesseractic prism (pent) (Same as 5-cube)	10	40	80	80	32
68	= r{4,3,3}×{ } Rectified tesseractic prism (rittip)	26	136	272	224	64
69	= t{4,3,3}×{ } Truncated tesseractic prism (tattip)	26	136	304	320	128
70	= rr{4,3,3}×{ } Cantellated tesseractic prism (srittip)	58	360	784	672	192
71	= t0,3{4,3,3}×{ } Runcinated tesseractic prism (sidpithip)	82	368	608	448	128
72	= 2t{4,3,3}×{ } Bitruncated tesseractic prism (tahp)	26	168	432	480	192
73	= tr{4,3,3}×{ } Cantitruncated tesseractic prism (grittip)	58	360	880	960	384
74	= t0,1,3{4,3,3}×{ } Runcitruncated tesseractic prism (prohp)	82	528	1216	1152	384
75	= t0,1,2,3{4,3,3}×{ } Omnitruncated tesseractic prism (gidpithip)	82	624	1696	1920	768
76	= {3,3,4}×{ } 16-cell prism (hexip)	18	64	88	56	16
77	= r{3,3,4}×{ } Rectified 16-cell prism (icope) (Same as 24-cell prism)	26	144	288	216	48
78	= t{3,3,4}×{ } Truncated 16-cell prism (thexip)	26	144	312	288	96
79	= rr{3,3,4}×{ } Cantellated 16-cell prism (ricope) (Same as rectified 24-cell prism)	50	336	768	672	192
80	= tr{3,3,4}×{ } Cantitruncated 16-cell prism (ticope) (Same as truncated 24-cell prism)	50	336	864	960	384
81	= t0,1,3{3,3,4}×{ } Runcitruncated 16-cell prism (prittip)	82	528	1216	1152	384
82	= sr{3,3,4}×{ } snub 24-cell prism (sadip)	146	768	1392	960	192
Nonuniform	rectified tesseractic alterprism (rita)	50	288	464	288	64
Nonuniform	truncated 16-cell alterprism (thexa)	26	168	384	336	96
Nonuniform	bitruncated tesseractic alterprism (taha)	50	288	624	576	192

F₄ × A₁

This prismatic family has 10 forms.

The A₁ x F₄ family has symmetry of order 2304 (2*1152). Three polytopes 85, 86 and 89 (green background) have double symmetry [[3,4,3],2], order 4608. The last one, snub 24-cell prism, (blue background) has [3⁺,4,3,2] symmetry, order 1152.

#	Coxeter diagram and Schläfli symbols Name	Element counts
		Facets	Cells	Faces	Edges	Vertices
[77]	= {3,4,3}×{ } 24-cell prism (icope)	26	144	288	216	48
[79]	= r{3,4,3}×{ } rectified 24-cell prism (ricope)	50	336	768	672	192
[80]	= t{3,4,3}×{ } truncated 24-cell prism (ticope)	50	336	864	960	384
83	= rr{3,4,3}×{ } cantellated 24-cell prism (sricope)	146	1008	2304	2016	576
84	= t0,3{3,4,3}×{ } runcinated 24-cell prism (spiccup)	242	1152	1920	1296	288
85	= 2t{3,4,3}×{ } bitruncated 24-cell prism (contip)	50	432	1248	1440	576
86	= tr{3,4,3}×{ } cantitruncated 24-cell prism (gricope)	146	1008	2592	2880	1152
87	= t0,1,3{3,4,3}×{ } runcitruncated 24-cell prism (pricope)	242	1584	3648	3456	1152
88	= t0,1,2,3{3,4,3}×{ } omnitruncated 24-cell prism (gippiccup)	242	1872	5088	5760	2304
[82]	= s{3,4,3}×{ } snub 24-cell prism (sadip)	146	768	1392	960	192

H₄ × A₁

This prismatic family has 15 forms:

The A₁ x H₄ family has symmetry of order 28800 (2*14400).

#	Coxeter diagram and Schläfli symbols Name	Element counts
		Facets	Cells	Faces	Edges	Vertices
89	= {5,3,3}×{ } 120-cell prism (hipe)	122	960	2640	3000	1200
90	= r{5,3,3}×{ } Rectified 120-cell prism (rahipe)	722	4560	9840	8400	2400
91	= t{5,3,3}×{ } Truncated 120-cell prism (thipe)	722	4560	11040	12000	4800
92	= rr{5,3,3}×{ } Cantellated 120-cell prism (srahip)	1922	12960	29040	25200	7200
93	= t0,3{5,3,3}×{ } Runcinated 120-cell prism (sidpixhip)	2642	12720	22080	16800	4800
94	= 2t{5,3,3}×{ } Bitruncated 120-cell prism (xhip)	722	5760	15840	18000	7200
95	= tr{5,3,3}×{ } Cantitruncated 120-cell prism (grahip)	1922	12960	32640	36000	14400
96	= t0,1,3{5,3,3}×{ } Runcitruncated 120-cell prism (prixip)	2642	18720	44880	43200	14400
97	= t0,1,2,3{5,3,3}×{ } Omnitruncated 120-cell prism (gidpixhip)	2642	22320	62880	72000	28800
98	= {3,3,5}×{ } 600-cell prism (exip)	602	2400	3120	1560	240
99	= r{3,3,5}×{ } Rectified 600-cell prism (roxip)	722	5040	10800	7920	1440
100	= t{3,3,5}×{ } Truncated 600-cell prism (texip)	722	5040	11520	10080	2880
101	= rr{3,3,5}×{ } Cantellated 600-cell prism (srixip)	1442	11520	28080	25200	7200
102	= tr{3,3,5}×{ } Cantitruncated 600-cell prism (grixip)	1442	11520	31680	36000	14400
103	= t0,1,3{3,3,5}×{ } Runcitruncated 600-cell prism (prahip)	2642	18720	44880	43200	14400

Duoprism prisms

Uniform duoprism prisms, {p}×{q}×{ }, form an infinite class for all integers p,q>2. {4}×{4}×{ } makes a lower symmetry form of the 5-cube.

The extended f-vector of {p}×{q}×{ } is computed as (p,p,1)*(q,q,1)*(2,1) = (2pq,5pq,4pq+2p+2q,3pq+3p+3q,p+q+2,1).

Coxeter diagram	Names	Element counts
		4-faces	Cells	Faces	Edges	Vertices
	{p}×{q}×{ } [9]	p+q+2	3pq+3p+3q	4pq+2p+2q	5pq	2pq
	{p}2×{ }	2(p+1)	3p(p+1)	4p(p+1)	5p2	2p2
	{3}2×{ }	8	36	48	45	18
	{4}2×{ } = 5-cube	10	40	80	80	32

Grand antiprism prism

The grand antiprism prism is the only known convex non-Wythoffian uniform 5-polytope. It has 200 vertices, 1100 edges, 1940 faces (40 pentagons, 500 squares, 1400 triangles), 1360 cells (600 tetrahedra, 40 pentagonal antiprisms, 700 triangular prisms, 20 pentagonal prisms), and 322 hypercells (2 grand antiprisms , 20 pentagonal antiprism prisms , and 300 tetrahedral prisms ).

#	Name	Element counts
		Facets	Cells	Faces	Edges	Vertices
104	grand antiprism prism (gappip) [10]	322	1360	1940	1100	200

Notes on the Wythoff construction for the uniform 5-polytopes

Construction of the reflective 5-dimensional uniform polytopes are done through a Wythoff construction process, and represented through a Coxeter diagram, where each node represents a mirror. Nodes are ringed to imply which mirrors are active. The full set of uniform polytopes generated are based on the unique permutations of ringed nodes. Uniform 5-polytopes are named in relation to the regular polytopes in each family. Some families have two regular constructors and thus may have two ways of naming them.

Here are the primary operators available for constructing and naming the uniform 5-polytopes.

The last operation, the snub, and more generally the alternation, are the operations that can create nonreflective forms. These are drawn with "hollow rings" at the nodes.

The prismatic forms and bifurcating graphs can use the same truncation indexing notation, but require an explicit numbering system on the nodes for clarity.

Operation	Extended Schläfli symbol		Coxeter diagram	Description
Parent	t0{p,q,r,s}	{p,q,r,s}		Any regular 5-polytope
Rectified	t1{p,q,r,s}	r{p,q,r,s}		The edges are fully truncated into single points. The 5-polytope now has the combined faces of the parent and dual.
Birectified	t2{p,q,r,s}	2r{p,q,r,s}		Birectification reduces faces to points, cells to their duals.
Trirectified	t3{p,q,r,s}	3r{p,q,r,s}		Trirectification reduces cells to points. (Dual rectification)
Quadrirectified	t4{p,q,r,s}	4r{p,q,r,s}		Quadrirectification reduces 4-faces to points. (Dual)
Truncated	t0,1{p,q,r,s}	t{p,q,r,s}		Each original vertex is cut off, with a new face filling the gap. Truncation has a degree of freedom, which has one solution that creates a uniform truncated 5-polytope. The 5-polytope has its original faces doubled in sides, and contains the faces of the dual.
Cantellated	t0,2{p,q,r,s}	rr{p,q,r,s}		In addition to vertex truncation, each original edge is beveled with new rectangular faces appearing in their place.
Runcinated	t0,3{p,q,r,s}			Runcination reduces cells and creates new cells at the vertices and edges.
Stericated	t0,4{p,q,r,s}	2r2r{p,q,r,s}		Sterication reduces facets and creates new facets (hypercells) at the vertices and edges in the gaps. (Same as expansion operation for 5-polytopes.)
Omnitruncated	t0,1,2,3,4{p,q,r,s}			All four operators, truncation, cantellation, runcination, and sterication are applied.
Half	h{2p,3,q,r}			Alternation, same as
Cantic	h2{2p,3,q,r}			Same as
Runcic	h3{2p,3,q,r}			Same as
Runcicantic	h2,3{2p,3,q,r}			Same as
Steric	h4{2p,3,q,r}			Same as
Steriruncic	h3,4{2p,3,q,r}			Same as
Stericantic	h2,4{2p,3,q,r}			Same as
Steriruncicantic	h2,3,4{2p,3,q,r}			Same as
Snub	s{p,2q,r,s}			Alternated truncation
Snub rectified	sr{p,q,2r,s}			Alternated truncated rectification
	ht0,1,2,3{p,q,r,s}			Alternated runcicantitruncation
Full snub	ht0,1,2,3,4{p,q,r,s}			Alternated omnitruncation

Regular and uniform honeycombs

Coxeter diagram correspondences between families and higher symmetry within diagrams. Nodes of the same color in each row represent identical mirrors. Black nodes are not active in the correspondence.

There are five fundamental affine Coxeter groups, and 13 prismatic groups that generate regular and uniform tessellations in Euclidean 4-space. ^{[11] [12]}

Fundamental groups

#	Coxeter group			Coxeter diagram	Forms
1	${\displaystyle {\tilde {A}}_{4}}$	[3[5]]	[(3,3,3,3,3)]		7
2	${\displaystyle {\tilde {C}}_{4}}$	[4,3,3,4]			19
3	${\displaystyle {\tilde {B}}_{4}}$	[4,3,31,1]	[4,3,3,4,1+]	=	23 (8 new)
4	${\displaystyle {\tilde {D}}_{4}}$	[31,1,1,1]	[1+,4,3,3,4,1+]	=	9 (0 new)
5	${\displaystyle {\tilde {F}}_{4}}$	[3,4,3,3]			31 (21 new)

There are three regular honeycombs of Euclidean 4-space:

• tesseractic honeycomb, with symbols {4,3,3,4}, = . There are 19 uniform honeycombs in this family.
• 24-cell honeycomb, with symbols {3,4,3,3}, . There are 31 reflective uniform honeycombs in this family, and one alternated form.
  • Truncated 24-cell honeycomb with symbols t{3,4,3,3},
  • Snub 24-cell honeycomb, with symbols s{3,4,3,3}, and constructed by four snub 24-cell, one 16-cell, and five 5-cells at each vertex.
• 16-cell honeycomb, with symbols {3,3,4,3},

Other families that generate uniform honeycombs:

• There are 23 uniquely ringed forms, 8 new ones in the 16-cell honeycomb family. With symbols h{4,3²,4} it is geometrically identical to the 16-cell honeycomb, =
• There are 7 uniquely ringed forms from the ${\displaystyle {\tilde {A}}_{4}}$, family, all new, including:
  • 4-simplex honeycomb
  • Truncated 4-simplex honeycomb
  • Omnitruncated 4-simplex honeycomb
• There are 9 uniquely ringed forms in the ${\displaystyle {\tilde {D}}_{4}}$: [3^1,1,1,1] family, two new ones, including the quarter tesseractic honeycomb, = , and the bitruncated tesseractic honeycomb, = .

Non-Wythoffian uniform tessellations in 4-space also exist by elongation (inserting layers), and gyration (rotating layers) from these reflective forms.

Prismatic groups

#	Coxeter group		Coxeter diagram
1	${\displaystyle {\tilde {C}}_{3}}$×${\displaystyle {\tilde {I}}_{1}}$	[4,3,4,2,∞]
2	${\displaystyle {\tilde {B}}_{3}}$×${\displaystyle {\tilde {I}}_{1}}$	[4,31,1,2,∞]
3	${\displaystyle {\tilde {A}}_{3}}$×${\displaystyle {\tilde {I}}_{1}}$	[3[4],2,∞]
4	${\displaystyle {\tilde {C}}_{2}}$×${\displaystyle {\tilde {I}}_{1}}$x${\displaystyle {\tilde {I}}_{1}}$	[4,4,2,∞,2,∞]
5	${\displaystyle {\tilde {H}}_{2}}$×${\displaystyle {\tilde {I}}_{1}}$x${\displaystyle {\tilde {I}}_{1}}$	[6,3,2,∞,2,∞]
6	${\displaystyle {\tilde {A}}_{2}}$×${\displaystyle {\tilde {I}}_{1}}$x${\displaystyle {\tilde {I}}_{1}}$	[3[3],2,∞,2,∞]
7	${\displaystyle {\tilde {I}}_{1}}$×${\displaystyle {\tilde {I}}_{1}}$x${\displaystyle {\tilde {I}}_{1}}$x${\displaystyle {\tilde {I}}_{1}}$	[∞,2,∞,2,∞,2,∞]
8	${\displaystyle {\tilde {A}}_{2}}$x${\displaystyle {\tilde {A}}_{2}}$	[3[3],2,3[3]]
9	${\displaystyle {\tilde {A}}_{2}}$×${\displaystyle {\tilde {B}}_{2}}$	[3[3],2,4,4]
10	${\displaystyle {\tilde {A}}_{2}}$×${\displaystyle {\tilde {G}}_{2}}$	[3[3],2,6,3]
11	${\displaystyle {\tilde {B}}_{2}}$×${\displaystyle {\tilde {B}}_{2}}$	[4,4,2,4,4]
12	${\displaystyle {\tilde {B}}_{2}}$×${\displaystyle {\tilde {G}}_{2}}$	[4,4,2,6,3]
13	${\displaystyle {\tilde {G}}_{2}}$×${\displaystyle {\tilde {G}}_{2}}$	[6,3,2,6,3]

Regular and uniform hyperbolic honeycombs

Hyperbolic compact groups

There are 5 compact hyperbolic Coxeter groups of rank 5, each generating uniform honeycombs in hyperbolic 4-space as permutations of rings of the Coxeter diagrams.

${\displaystyle {\widehat {AF}}_{4}}$ = [(3,3,3,3,4)]:

${\displaystyle {\bar {DH}}_{4}}$ = [5,3,31,1]:

${\displaystyle {\bar {H}}_{4}}$ = [3,3,3,5]: ${\displaystyle {\bar {BH}}_{4}}$ = [4,3,3,5]: ${\displaystyle {\bar {K}}_{4}}$ = [5,3,3,5]:

There are 5 regular compact convex hyperbolic honeycombs in H⁴ space: ^[13]

Compact regular convex hyperbolic honeycombs

Honeycomb name	Schläfli Symbol {p,q,r,s}	Coxeter diagram	Facet type {p,q,r}	Cell type {p,q}	Face type {p}	Face figure {s}	Edge figure {r,s}	Vertex figure {q,r,s}	Dual
Order-5 5-cell (pente)	{3,3,3,5}		{3,3,3}	{3,3}	{3}	{5}	{3,5}	{3,3,5}	{5,3,3,3}
Order-3 120-cell (hitte)	{5,3,3,3}		{5,3,3}	{5,3}	{5}	{3}	{3,3}	{3,3,3}	{3,3,3,5}
Order-5 tesseractic (pitest)	{4,3,3,5}		{4,3,3}	{4,3}	{4}	{5}	{3,5}	{3,3,5}	{5,3,3,4}
Order-4 120-cell (shitte)	{5,3,3,4}		{5,3,3}	{5,3}	{5}	{4}	{3,4}	{3,3,4}	{4,3,3,5}
Order-5 120-cell (phitte)	{5,3,3,5}		{5,3,3}	{5,3}	{5}	{5}	{3,5}	{3,3,5}	Self-dual

There are also 4 regular compact hyperbolic star-honeycombs in H⁴ space:

Compact regular hyperbolic star-honeycombs

Honeycomb name	Schläfli Symbol {p,q,r,s}	Coxeter diagram	Facet type {p,q,r}	Cell type {p,q}	Face type {p}	Face figure {s}	Edge figure {r,s}	Vertex figure {q,r,s}	Dual
Order-3 small stellated 120-cell	{5/2,5,3,3}		{5/2,5,3}	{5/2,5}	{5}	{5}	{3,3}	{5,3,3}	{3,3,5,5/2}
Order-5/2 600-cell	{3,3,5,5/2}		{3,3,5}	{3,3}	{3}	{5/2}	{5,5/2}	{3,5,5/2}	{5/2,5,3,3}
Order-5 icosahedral 120-cell	{3,5,5/2,5}		{3,5,5/2}	{3,5}	{3}	{5}	{5/2,5}	{5,5/2,5}	{5,5/2,5,3}
Order-3 great 120-cell	{5,5/2,5,3}		{5,5/2,5}	{5,5/2}	{5}	{3}	{5,3}	{5/2,5,3}	{3,5,5/2,5}

Hyperbolic paracompact groups

There are 9 paracompact hyperbolic Coxeter groups of rank 5, each generating uniform honeycombs in 4-space as permutations of rings of the Coxeter diagrams. Paracompact groups generate honeycombs with infinite facets or vertex figures.

${\displaystyle {\bar {P}}_{4}}$ = [3,3[4]]: ${\displaystyle {\bar {BP}}_{4}}$ = [4,3[4]]: ${\displaystyle {\bar {FR}}_{4}}$ = [(3,3,4,3,4)]: ${\displaystyle {\bar {DP}}_{4}}$ = [3[3]×[]]:

${\displaystyle {\bar {N}}_{4}}$ = [4,/3\,3,4]: ${\displaystyle {\bar {O}}_{4}}$ = [3,4,31,1]: ${\displaystyle {\bar {S}}_{4}}$ = [4,32,1]: ${\displaystyle {\bar {M}}_{4}}$ = [4,31,1,1]:

${\displaystyle {\bar {R}}_{4}}$ = [3,4,3,4]:

Notes

1. T. Gosset: On the Regular and Semi-Regular Figures in Space of n Dimensions, Messenger of Mathematics, Macmillan, 1900
2. Multidimensional Glossary, George Olshevsky
3. Bowers, Jonathan (2000). "Uniform Polychora" (PDF). In Reza Sarhagi (ed.). Bridges 2000. Bridges Conference. pp. 239–246.
4. Uniform Polytera, Jonathan Bowers
5. Uniform polytope
6. ACW (May 24, 2012), "Convex uniform 5-polytopes", Open Problem Garden, archived from the original on October 5, 2016, retrieved 2016-10-04
7. Regular and semi-regular polytopes III, p.315 Three finite groups of 5-dimensions
8. Coxeter, Regular polytopes, §12.6 The number of reflections, equation 12.61
9. "N,k-dippip".
10. "Gappip".
11. Regular polytopes, p.297. Table IV, Fundamental regions for irreducible groups generated by reflections.
12. Regular and Semiregular polytopes, II, pp.298-302 Four-dimensional honeycombs
13. Coxeter, The Beauty of Geometry: Twelve Essays, Chapter 10: Regular honeycombs in hyperbolic space, Summary tables IV p213

References

• T. Gosset: On the Regular and Semi-Regular Figures in Space of n Dimensions, Messenger of Mathematics, Macmillan, 1900 (3 regular and one semiregular 4-polytope)
• A. Boole Stott: Geometrical deduction of semiregular from regular polytopes and space fillings, Verhandelingen of the Koninklijke academy van Wetenschappen width unit Amsterdam, Eerste Sectie 11,1, Amsterdam, 1910
• H.S.M. Coxeter:
  • H.S.M. Coxeter, Regular Polytopes, 3rd Edition, Dover New York, 1973 (p. 297 Fundamental regions for irreducible groups generated by reflections, Spherical and Euclidean)
  • H.S.M. Coxeter, The Beauty of Geometry: Twelve Essays (Chapter 10: Regular honeycombs in hyperbolic space, Summary tables IV p213)
• Kaleidoscopes: Selected Writings of H.S.M. Coxeter, edited by F. Arthur Sherk, Peter McMullen, Anthony C. Thompson, Asia Ivic Weiss, Wiley-Interscience Publication, 1995, ISBN   978-0-471-01003-6
  • (Paper 22) H.S.M. Coxeter, Regular and Semi Regular Polytopes I, [Math. Zeit. 46 (1940) 380-407, MR 2,10]
  • (Paper 23) H.S.M. Coxeter, Regular and Semi-Regular Polytopes II, [Math. Zeit. 188 (1985) 559-591] (p. 287 5D Euclidean groups, p. 298 Four-dimensionsal honeycombs)
  • (Paper 24) H.S.M. Coxeter, Regular and Semi-Regular Polytopes III, [Math. Zeit. 200 (1988) 3-45]
• N.W. Johnson: The Theory of Uniform Polytopes and Honeycombs, Ph.D. Dissertation, University of Toronto, 1966
• James E. Humphreys, Reflection Groups and Coxeter Groups, Cambridge studies in advanced mathematics, 29 (1990) (Page 141, 6.9 List of hyperbolic Coxeter groups, figure 2)

External links

• Klitzing, Richard. "5D uniform polytopes (polytera)". – includes nonconvex forms as well as the duplicate constructions from the B₅ and D₅ families

v t e Fundamental convex regular and uniform polytopes in dimensions 2–10
Family	An	Bn	I2(p) / Dn	E6 / E7 / E8 / F4 / G2	Hn
Regular polygon	Triangle	Square	p-gon	Hexagon	Pentagon
Uniform polyhedron	Tetrahedron	Octahedron • Cube	Demicube		Dodecahedron • Icosahedron
Uniform polychoron	Pentachoron	16-cell • Tesseract	Demitesseract	24-cell	120-cell • 600-cell
Uniform 5-polytope	5-simplex	5-orthoplex • 5-cube	5-demicube
Uniform 6-polytope	6-simplex	6-orthoplex • 6-cube	6-demicube	122 • 221
Uniform 7-polytope	7-simplex	7-orthoplex • 7-cube	7-demicube	132 • 231 • 321
Uniform 8-polytope	8-simplex	8-orthoplex • 8-cube	8-demicube	142 • 241 • 421
Uniform 9-polytope	9-simplex	9-orthoplex • 9-cube	9-demicube
Uniform 10-polytope	10-simplex	10-orthoplex • 10-cube	10-demicube
Uniform n-polytope	n-simplex	n-orthoplex • n-cube	n-demicube	1k2 • 2k1 • k21	n-pentagonal polytope
Topics: Polytope families • Regular polytope • List of regular polytopes and compounds

v t e Fundamental convex regular and uniform honeycombs in dimensions 2–9
Space	Family	${\displaystyle {\tilde {A}}_{n-1}}$	${\displaystyle {\tilde {C}}_{n-1}}$	${\displaystyle {\tilde {B}}_{n-1}}$	${\displaystyle {\tilde {D}}_{n-1}}$	${\displaystyle {\tilde {G}}_{2}}$ / ${\displaystyle {\tilde {F}}_{4}}$ / ${\displaystyle {\tilde {E}}_{n-1}}$
E2	Uniform tiling	{3[3]}	δ3	hδ3	qδ3	Hexagonal
E3	Uniform convex honeycomb	{3[4]}	δ4	hδ4	qδ4
E4	Uniform 4-honeycomb	{3[5]}	δ5	hδ5	qδ5	24-cell honeycomb
E5	Uniform 5-honeycomb	{3[6]}	δ6	hδ6	qδ6
E6	Uniform 6-honeycomb	{3[7]}	δ7	hδ7	qδ7	222
E7	Uniform 7-honeycomb	{3[8]}	δ8	hδ8	qδ8	133 • 331
E8	Uniform 8-honeycomb	{3[9]}	δ9	hδ9	qδ9	152 • 251 • 521
E9	Uniform 9-honeycomb	{3[10]}	δ10	hδ10	qδ10
E10	Uniform 10-honeycomb	{3[11]}	δ11	hδ11	qδ11
En-1	Uniform (n-1)-honeycomb	{3[n]}	δn	hδn	qδn	1k2 • 2k1 • k21