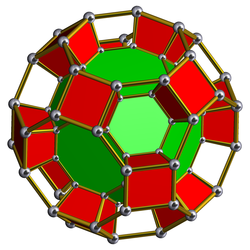
In geometry, the rhombicuboctahedron, or small rhombicuboctahedron, is a polyhedron with eight triangular, six square, and twelve rectangular faces. There are 24 identical vertices, with one triangle, one square, and two rectangles meeting at each one. If all the rectangles are themselves square, it is an Archimedean solid. The polyhedron has octahedral symmetry, like the cube and octahedron. Its dual is called the deltoidal icositetrahedron or trapezoidal icositetrahedron, although its faces are not really true trapezoids.

In geometry, a uniform 4-polytope is a 4-dimensional polytope which is vertex-transitive and whose cells are uniform polyhedra, and faces are regular polygons.

In geometry of 4 dimensions or higher, a double prism or duoprism is a polytope resulting from the Cartesian product of two polytopes, each of two dimensions or higher. The Cartesian product of an n-polytope and an m-polytope is an (n+m)-polytope, where n and m are dimensions of 2 (polygon) or higher.

In four-dimensional geometry, a runcinated 5-cell is a convex uniform 4-polytope, being a runcination of the regular 5-cell.

In four-dimensional geometry, a runcinated tesseract is a convex uniform 4-polytope, being a runcination of the regular tesseract.

In four-dimensional geometry, the rectified 5-cell is a uniform 4-polytope composed of 5 regular tetrahedral and 5 regular octahedral cells. Each edge has one tetrahedron and two octahedra. Each vertex has two tetrahedra and three octahedra. In total it has 30 triangle faces, 30 edges, and 10 vertices. Each vertex is surrounded by 3 octahedra and 2 tetrahedra; the vertex figure is a triangular prism.

The cubic honeycomb or cubic cellulation is the only proper regular space-filling tessellation in Euclidean 3-space made up of cubic cells. It has 4 cubes around every edge, and 8 cubes around each vertex. Its vertex figure is a regular octahedron. It is a self-dual tessellation with Schläfli symbol {4,3,4}. John Horton Conway called this honeycomb a cubille.

The tetrahedral-octahedral honeycomb, alternated cubic honeycomb is a quasiregular space-filling tessellation in Euclidean 3-space. It is composed of alternating regular octahedra and tetrahedra in a ratio of 1:2.

In hyperbolic geometry, the order-5 cubic honeycomb is one of four compact regular space-filling tessellations in hyperbolic 3-space. With Schläfli symbol {4,3,5}, it has five cubes {4,3} around each edge, and 20 cubes around each vertex. It is dual with the order-4 dodecahedral honeycomb.

In geometry, the icosahedral honeycomb is one of four compact, regular, space-filling tessellations in hyperbolic 3-space. With Schläfli symbol {3,5,3}, there are three icosahedra around each edge, and 12 icosahedra around each vertex, in a regular dodecahedral vertex figure.

In geometry, a truncated 24-cell is a uniform 4-polytope formed as the truncation of the regular 24-cell.

In geometry, the rectified 24-cell or rectified icositetrachoron is a uniform 4-dimensional polytope, which is bounded by 48 cells: 24 cubes, and 24 cuboctahedra. It can be obtained by rectification of the 24-cell, reducing its octahedral cells to cubes and cuboctahedra.

In four-dimensional geometry, a cantellated 5-cell is a convex uniform 4-polytope, being a cantellation of the regular 5-cell.

In four-dimensional geometry, a cantellated 24-cell is a convex uniform 4-polytope, being a cantellation of the regular 24-cell.

In four-dimensional geometry, a runcinated 24-cell is a convex uniform 4-polytope, being a runcination of the regular 24-cell.
In 4-dimensional geometry, a truncated octahedral prism or omnitruncated tetrahedral prism is a convex uniform 4-polytope. This 4-polytope has 16 cells It has 64 faces, and 96 edges and 48 vertices.
In geometry, a rhombicuboctahedral prism is a convex uniform polychoron.

In geometry, a truncated icosidodecahedral prism or great rhombicosidodecahedral prism is a convex uniform 4-polytope.

In the geometry of hyperbolic 3-space, the square tiling honeycomb is one of 11 paracompact regular honeycombs. It is called paracompact because it has infinite cells, whose vertices exist on horospheres and converge to a single ideal point at infinity. Given by Schläfli symbol {4,4,3}, it has three square tilings, {4,4}, around each edge, and six square tilings around each vertex, in a cubic {4,3} vertex figure.