| Snub 24-cell honeycomb | |
|---|---|
| (No image) | |
| Type | Uniform 4-honeycomb |
| Schläfli symbols | s{3,4,3,3} sr{3,3,4,3} 2sr{4,3,3,4} 2sr{4,3,31,1} s{31,1,1,1} |
| Coxeter diagrams |
|
| 4-face type | snub 24-cell 16-cell 5-cell |
| Cell type | {3,3} {3,5} |
| Face type | triangle {3} |
| Vertex figure |  Irregular decachoron |
| Symmetries | [3+,4,3,3] [3,4,(3,3)+] [4,(3,3)+,4] [4,(3,31,1)+] [31,1,1,1]+ |
| Properties | Vertex transitive, nonWythoffian |
In four-dimensional Euclidean geometry, the snub 24-cell honeycomb, or snub icositetrachoric honeycomb is a uniform space-filling tessellation (or honeycomb) by snub 24-cells, 16-cells, and 5-cells. It was discovered by Thorold Gosset with his 1900 paper of semiregular polytopes. It is not semiregular by Gosset's definition of regular facets, but all of its cells (ridges) are regular, either tetrahedra or icosahedra.

A four-dimensional space or 4D space is a mathematical extension of the concept of three-dimensional or 3D space. Three-dimensional space is the simplest possible generalization of the observation that one only needs three numbers, called dimensions, to describe the sizes or locations of objects in the everyday world. For example, the volume of a rectangular box is found by measuring its length, width, and height.

Euclidean geometry is a mathematical system attributed to Alexandrian Greek mathematician Euclid, which he described in his textbook on geometry: the Elements. Euclid's method consists in assuming a small set of intuitively appealing axioms, and deducing many other propositions (theorems) from these. Although many of Euclid's results had been stated by earlier mathematicians, Euclid was the first to show how these propositions could fit into a comprehensive deductive and logical system. The Elements begins with plane geometry, still taught in secondary school as the first axiomatic system and the first examples of formal proof. It goes on to the solid geometry of three dimensions. Much of the Elements states results of what are now called algebra and number theory, explained in geometrical language.

A tessellation of a flat surface is the tiling of a plane using one or more geometric shapes, called tiles, with no overlaps and no gaps. In mathematics, tessellations can be generalized to higher dimensions and a variety of geometries.
Contents
It can be seen as an alternation of a truncated 24-cell honeycomb, and can be represented by Schläfli symbol s{3,4,3,3}, s{31,1,1,1}, and 3 other snub constructions.

In geometry, an alternation or partial truncation, is an operation on a polygon, polyhedron, tiling, or higher dimensional polytope that removes alternate vertices.
In four-dimensional Euclidean geometry, the truncated 24-cell honeycomb is a uniform space-filling honeycomb. It can be seen as a truncation of the regular 24-cell honeycomb, containing tesseract and truncated 24-cell cells.

In geometry, the Schläfli symbol is a notation of the form {p,q,r,...} that defines regular polytopes and tessellations.
It is defined by an irregular decachoron vertex figure (10-celled 4-polytope), faceted by four snub 24-cells, one 16-cell, and five 5-cells. The vertex figure can be seen topologically as a modified tetrahedral prism, where one of the tetrahedra is subdivided at mid-edges into a central octahedron and four corner tetrahedra. Then the four side-facets of the prism, the triangular prisms become tridiminished icosahedra.

In geometry, a vertex figure, broadly speaking, is the figure exposed when a corner of a polyhedron or polytope is sliced off.
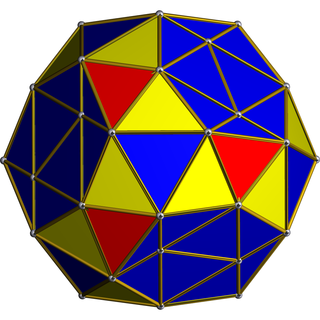
In geometry, the snub 24-cell or snub disicositetrachoron is a convex uniform 4-polytope composed of 120 regular tetrahedral and 24 icosahedral cells. Five tetrahedra and three icosahedra meet at each vertex. In total it has 480 triangular faces, 432 edges, and 96 vertices.

In four-dimensional geometry, a 16-cell is a regular convex 4-polytope. It is one of the six regular convex 4-polytopes first described by the Swiss mathematician Ludwig Schläfli in the mid-19th century. It is also called C16, hexadecachoron, or hexdecahedroid.




















