
In geometry, a convex uniform honeycomb is a uniform tessellation which fills three-dimensional Euclidean space with non-overlapping convex uniform polyhedral cells.

The cubic honeycomb or cubic cellulation is the only proper regular space-filling tessellation in Euclidean 3-space made up of cubic cells. It has 4 cubes around every edge, and 8 cubes around each vertex. Its vertex figure is a regular octahedron. It is a self-dual tessellation with Schläfli symbol {4,3,4}. John Horton Conway called this honeycomb a cubille.

The tetrahedral-octahedral honeycomb, alternated cubic honeycomb is a quasiregular space-filling tessellation in Euclidean 3-space. It is composed of alternating regular octahedra and tetrahedra in a ratio of 1:2.

In eight-dimensional geometry, an eight-dimensional polytope or 8-polytope is a polytope contained by 7-polytope facets. Each 6-polytope ridge being shared by exactly two 7-polytope facets.

In seven-dimensional geometry, a 7-polytope is a polytope contained by 6-polytope facets. Each 5-polytope ridge being shared by exactly two 6-polytope facets.

In nine-dimensional geometry, a nine-dimensional polytope or 9-polytope is a polytope contained by 8-polytope facets. Each 7-polytope ridge being shared by exactly two 8-polytope facets.

In six-dimensional geometry, a uniform 6-polytope is a six-dimensional uniform polytope. A uniform polypeton is vertex-transitive, and all facets are uniform 5-polytopes.

In four-dimensional euclidean geometry, the tesseractic honeycomb is one of the three regular space-filling tessellations, represented by Schläfli symbol {4,3,3,4}, and consisting of a packing of tesseracts (4-hypercubes).

In four-dimensional Euclidean geometry, the 16-cell honeycomb is one of the three regular space-filling tessellations, represented by Schläfli symbol {3,3,4,3}, and constructed by a 4-dimensional packing of 16-cell facets, three around every face.
In geometry, the 5-cubic honeycomb or penteractic honeycomb is the only regular space-filling tessellation in Euclidean 5-space. Four 5-cubes meet at each cubic cell, and it is more explicitly called an order-4 penteractic honeycomb.
The 5-demicube honeycomb is a uniform space-filling tessellation in Euclidean 5-space. It is constructed as an alternation of the regular 5-cube honeycomb.
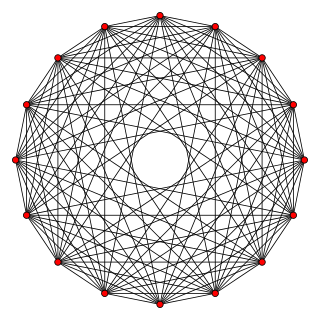
In geometry, an 8-orthoplex or 8-cross polytope is a regular 8-polytope with 16 vertices, 112 edges, 448 triangle faces, 1120 tetrahedron cells, 1792 5-cells 4-faces, 1792 5-faces, 1024 6-faces, and 256 7-faces.
In geometry, a hypercubic honeycomb is a family of regular honeycombs (tessellations) in n-dimensional spaces with the Schläfli symbols {4,3...3,4} and containing the symmetry of Coxeter group Rn for n ≥ 3.
The 6-demicubic honeycomb or demihexeractic honeycomb is a uniform space-filling tessellation in Euclidean 6-space. It is constructed as an alternation of the regular 6-cube honeycomb.
The 7-cubic honeycomb or hepteractic honeycomb is the only regular space-filling tessellation in Euclidean 7-space.
In geometry, the 8-cubic honeycomb or octeractic honeycomb is the only regular space-filling tessellation in Euclidean 8-space.
The 8-demicubic honeycomb, or demiocteractic honeycomb is a uniform space-filling tessellation in Euclidean 8-space. It is constructed as an alternation of the regular 8-cubic honeycomb.

In geometry, a uniform 5-polytope is a five-dimensional uniform polytope. By definition, a uniform 5-polytope is vertex-transitive and constructed from uniform 4-polytope facets.

In ten-dimensional geometry, a 10-polytope is a 10-dimensional polytope whose boundary consists of 9-polytope facets, exactly two such facets meeting at each 8-polytope ridge.
In geometry, the 222 honeycomb is a uniform tessellation of the six-dimensional Euclidean space. It can be represented by the Schläfli symbol {3,3,32,2}. It is constructed from 221 facets and has a 122 vertex figure, with 54 221 polytopes around every vertex.





















