In geometry, the Schläfli symbol is a notation of the form that defines regular polytopes and tessellations.

In geometry, a vertex figure, broadly speaking, is the figure exposed when a corner of a general n-polytope is sliced off.

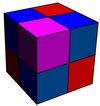
The cubic honeycomb or cubic cellulation is the only proper regular space-filling tessellation in Euclidean 3-space made up of cubic cells. It has 4 cubes around every edge, and 8 cubes around each vertex. Its vertex figure is a regular octahedron. It is a self-dual tessellation with Schläfli symbol {4,3,4}. John Horton Conway called this honeycomb a cubille.

The tetrahedral-octahedral honeycomb, alternated cubic honeycomb is a quasiregular space-filling tessellation in Euclidean 3-space. It is composed of alternating regular octahedra and tetrahedra in a ratio of 1:2.

The quarter cubic honeycomb, quarter cubic cellulation or bitruncated alternated cubic honeycomb is a space-filling tessellation in Euclidean 3-space. It is composed of tetrahedra and truncated tetrahedra in a ratio of 1:1. It is called "quarter-cubic" because its symmetry unit – the minimal block from which the pattern is developed by reflections – is four times that of the cubic honeycomb.

In four-dimensional euclidean geometry, the tesseractic honeycomb is one of the three regular space-filling tessellations, represented by Schläfli symbol {4,3,3,4}, and consisting of a packing of tesseracts (4-hypercubes).

In four-dimensional Euclidean geometry, the 16-cell honeycomb is one of the three regular space-filling tessellations, represented by Schläfli symbol {3,3,4,3}, and constructed by a 4-dimensional packing of 16-cell facets, three around every face.
The 5-demicube honeycomb is a uniform space-filling tessellation in Euclidean 5-space. It is constructed as an alternation of the regular 5-cube honeycomb.
The 7-demicubic honeycomb, or demihepteractic honeycomb is a uniform space-filling tessellation in Euclidean 7-space. It is constructed as an alternation of the regular 7-cubic honeycomb.
The 8-demicubic honeycomb, or demiocteractic honeycomb is a uniform space-filling tessellation in Euclidean 8-space. It is constructed as an alternation of the regular 8-cubic honeycomb.

In geometry, the alternated hypercube honeycomb is a dimensional infinite series of honeycombs, based on the hypercube honeycomb with an alternation operation. It is given a Schläfli symbol h{4,3...3,4} representing the regular form with half the vertices removed and containing the symmetry of Coxeter group for n ≥ 4. A lower symmetry form can be created by removing another mirror on an order-4 peak.
In four-dimensional Euclidean geometry, the 4-simplex honeycomb, 5-cell honeycomb or pentachoric-dispentachoric honeycomb is a space-filling tessellation honeycomb. It is composed of 5-cells and rectified 5-cells facets in a ratio of 1:1.
In geometry an omnitruncated simplicial honeycomb or omnitruncated n-simplex honeycomb is an n-dimensional uniform tessellation, based on the symmetry of the affine Coxeter group. Each is composed of omnitruncated simplex facets. The vertex figure for each is an irregular n-simplex.

In geometry, the simplicial honeycomb is a dimensional infinite series of honeycombs, based on the affine Coxeter group symmetry. It is represented by a Coxeter-Dynkin diagram as a cyclic graph of n + 1 nodes with one node ringed. It is composed of n-simplex facets, along with all rectified n-simplices. It can be thought of as an n-dimensional hypercubic honeycomb that has been subdivided along all hyperplanes , then stretched along its main diagonal until the simplices on the ends of the hypercubes become regular. The vertex figure of an n-simplex honeycomb is an expanded n-simplex.

In the field of hyperbolic geometry, the order-4 hexagonal tiling honeycomb arises as one of 11 regular paracompact honeycombs in 3-dimensional hyperbolic space. It is paracompact because it has cells composed of an infinite number of faces. Each cell is a hexagonal tiling whose vertices lie on a horosphere: a flat plane in hyperbolic space that approaches a single ideal point at infinity.

The order-6 cubic honeycomb is a paracompact regular space-filling tessellation in hyperbolic 3-space. It is paracompact because it has vertex figures composed of an infinite number of facets, with all vertices as ideal points at infinity. With Schläfli symbol {4,3,6}, the honeycomb has six ideal cubes meeting along each edge. Its vertex figure is an infinite triangular tiling. Its dual is the order-4 hexagonal tiling honeycomb.

In the geometry of hyperbolic 3-space, the square tiling honeycomb is one of 11 paracompact regular honeycombs. It is called paracompact because it has infinite cells, whose vertices exist on horospheres and converge to a single ideal point at infinity. Given by Schläfli symbol {4,4,3}, it has three square tilings, {4,4}, around each edge, and six square tilings around each vertex, in a cubic {4,3} vertex figure.

In geometry, the quarter hypercubic honeycomb is a dimensional infinite series of honeycombs, based on the hypercube honeycomb. It is given a Schläfli symbol q{4,3...3,4} or Coxeter symbol qδ4 representing the regular form with three quarters of the vertices removed and containing the symmetry of Coxeter group for n ≥ 5, with = and for quarter n-cubic honeycombs = .
In four-dimensional Euclidean geometry, the rectified tesseractic honeycomb is a uniform space-filling tessellation in Euclidean 4-space. It is constructed by a rectification of a tesseractic honeycomb which creates new vertices on the middle of all the original edges, rectifying the cells into rectified tesseracts, and adding new 16-cell facets at the original vertices. Its vertex figure is an octahedral prism, {3,4}×{}.