Alternated hypercubic honeycomb

Last updated March 08, 2019

An alternated square tiling or checkerboard pattern. or	An expanded square tiling.
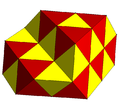A partially filled alternated cubic honeycomb with tetrahedral and octahedral cells. 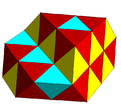or	A subsymmetry colored alternated cubic honeycomb.

In geometry, the alternated hypercube honeycomb (or demicubic honeycomb) is a dimensional infinite series of honeycombs, based on the hypercube honeycomb with an alternation operation. It is given a Schläfli symbol h{4,3...3,4} representing the regular form with half the vertices removed and containing the symmetry of Coxeter group ${\tilde {B}}_{n-1}$ for n ≥ 4. A lower symmetry form ${\tilde {D}}_{n-1}$ can be created by removing another mirror on an order-4 peak.^[1]

Geometry is a branch of mathematics concerned with questions of shape, size, relative position of figures, and the properties of space. A mathematician who works in the field of geometry is called a geometer.

In geometry, a honeycomb is a space filling or close packing of polyhedral or higher-dimensional cells, so that there are no gaps. It is an example of the more general mathematical tiling or tessellation in any number of dimensions. Its dimension can be clarified as n-honeycomb for a honeycomb of n-dimensional space.

In geometry, an alternation or partial truncation, is an operation on a polygon, polyhedron, tiling, or higher dimensional polytope that removes alternate vertices.

The alternated hypercube facets become demihypercubes, and the deleted vertices create new orthoplex facets. The vertex figure for honeycombs of this family are rectified orthoplexes.

Demihypercube polytope constructed from alternation of an hypercube

In geometry, demihypercubes are a class of n-polytopes constructed from alternation of an n-hypercube, labeled as hγ_n for being half of the hypercube family, γ_n. Half of the vertices are deleted and new facets are formed. The 2n facets become 2n(n-1)-demicubes, and 2ⁿ(n-1)-simplex facets are formed in place of the deleted vertices.

Vertex figure figure exposed when a corner of a polyhedron or polytope is sliced off

In geometry, a vertex figure, broadly speaking, is the figure exposed when a corner of a polyhedron or polytope is sliced off.

Rectification (geometry) process of truncating a polytope by marking the midpoints of all its edges, and cutting off its vertices at those points

In Euclidean geometry, rectification or complete-truncation is the process of truncating a polytope by marking the midpoints of all its edges, and cutting off its vertices at those points. The resulting polytope will be bounded by vertex figure facets and the rectified facets of the original polytope.

These are also named as hδ_n for an (n-1)-dimensional honeycomb.

hδ_n	Name	Schläfli symbol	Symmetry family
			${\tilde {B}}_{n-1}$ [4,3^n-4,3^1,1]	${\tilde {D}}_{n-1}$ [3^1,1,3^n-5,3^1,1]
			Coxeter-Dynkin diagrams by family
hδ₂	Apeirogon	{∞}
hδ₃	Alternated square tiling (Same as {4,4})	h{4,4}=t₁{4,4} t_0,2{4,4}
hδ₄	Alternated cubic honeycomb	h{4,3,4} {3^1,1,4}
hδ₅	16-cell tetracomb (Same as {3,3,4,3})	h{4,3²,4} {3^1,1,3,4} {3^1,1,1,1}
hδ₆	5-demicube honeycomb	h{4,3³,4} {3^1,1,3²,4} {3^1,1,3,3^1,1}
hδ₇	6-demicube honeycomb	h{4,3⁴,4} {3^1,1,3³,4} {3^1,1,3²,3^1,1}
hδ₈	7-demicube honeycomb	h{4,3⁵,4} {3^1,1,3⁴,4} {3^1,1,3³,3^1,1}
hδ₉	8-demicube honeycomb	h{4,3⁶,4} {3^1,1,3⁵,4} {3^1,1,3⁴,3^1,1}

hδ_n	n-demicubic honeycomb	h{4,3^n-3,4} {3^1,1,3^n-4,4} {3^1,1,3^n-5,3^1,1}	...

Related Research Articles

In eight-dimensional geometry, an eight-dimensional polytope or 8-polytope is a polytope contained by 7-polytope facets. Each 6-polytope ridge being shared by exactly two 7-polytope facets.

In seven-dimensional geometry, a 7-polytope is a polytope contained by 6-polytope facets. Each 5-polytope ridge being shared by exactly two 6-polytope facets.

In six-dimensional geometry, a uniform polypeton is a six-dimensional uniform polytope. A uniform polypeton is vertex-transitive, and all facets are uniform 5-polytopes.

In five-dimensional geometry, a 5-cube is a name for a five-dimensional hypercube with 32 vertices, 80 edges, 80 square faces, 40 cubic cells, and 10 tesseract 4-faces.

In five-dimensional geometry, a demipenteract or 5-demicube is a semiregular 5-polytope, constructed from a 5-hypercube (penteract) with alternated vertices removed.

In five-dimensional geometry, a 5-orthoplex, or 5-cross polytope, is a five-dimensional polytope with 10 vertices, 40 edges, 80 triangle faces, 80 tetrahedron cells, 32 5-cell 4-faces.

The 5-cubic honeycomb or penteractic honeycomb is the only regular space-filling tessellation in Euclidean 5-space. Four 5-cubes meet at each cubic cell, and it is more explicitly called an order-4 penteractic honeycomb.

The 5-demicube honeycomb, or demipenteractic honeycomb is a uniform space-filling tessellation in Euclidean 5-space. It is constructed as an alternation of the regular 5-cube honeycomb.

In geometry, a 6-demicube or demihexteract is a uniform 6-polytope, constructed from a 6-cube (hexeract) with alternated vertices removed. It is part of a dimensionally infinite family of uniform polytopes called demihypercubes.

In geometry, a hypercubic honeycomb is a family of regular honeycombs (tessellations) in n-dimensions with the Schläfli symbols {4,3...3,4} and containing the symmetry of Coxeter group R_n for n>=3.

The 6-cubic honeycomb or hexeractic honeycomb is the only regular space-filling tessellation in Euclidean 6-space.

The 7-cubic honeycomb or hepteractic honeycomb is the only regular space-filling tessellation in Euclidean 7-space.

The 8-cubic honeycomb or octeractic honeycomb is the only regular space-filling tessellation in Euclidean 8-space.

The 8-demicubic honeycomb, or demiocteractic honeycomb is a uniform space-filling tessellation in Euclidean 8-space. It is constructed as an alternation of the regular 8-cubic honeycomb.

In geometry, the 2₂₂ honeycomb is a uniform tessellation of the six-dimensional Euclidean space. It can be represented by the Schläfli symbol {3,3,3^2,2}. It is constructed from 2₂₁ facets and has a 1₂₂ vertex figure, with 54 2₂₁ polytopes around every vertex.

In 7-dimensional geometry, 1₃₃ is a uniform honeycomb, also given by Schläfli symbol {3,3^3,3}, and is composed of 1₃₂ facets.

In geometry, the 5₂₁ honeycomb is a uniform tessellation of 8-dimensional Euclidean space. The symbol 5₂₁ is from Coxeter, named for the length of the 3 branches of its Coxeter-Dynkin diagram.

In geometry, the simplectic honeycomb is a dimensional infinite series of honeycombs, based on the $affine Coxeter group symmetry. It is given a Schläfli symbol {3 [n+1]}, and is represented by a Coxeter-Dynkin diagram as a cyclic graph of n+1 nodes with one node ringed. It is composed of n-simplex facets, along with all rectified n-simplices. It can be thought of as an n-dimensional hypercubic honeycomb that has been subdivided along all hyperplanes, then stretched along its main diagonal until the simplices on the ends of the hypercubes become regular. The vertex figure of an n-simplex honeycomb is an expanded n-simplex.$

In geometry, the quarter hypercubic honeycomb is a dimensional infinite series of honeycombs, based on the hypercube honeycomb. It is given a Schläfli symbol q{4,3...3,4} or Coxeter symbol qδ₄ representing the regular form with three quarters of the vertices removed and containing the symmetry of Coxeter group $for n \geq 5, with = and for quarter n-cubic honeycombs = .$

References

↑ Regular and semi-regular polytopes III, p.318-319

Coxeter, H.S.M. Regular Polytopes , (3rd edition, 1973), Dover edition, ISBN 0-486-61480-8
1. pp. 122–123, 1973. (The lattice of hypercubes γ_n form the cubic honeycombs, δ_n+1)
2. pp. 154–156: Partial truncation or alternation, represented by h prefix: h{4,4}={4,4}; h{4,3,4}={3^1,1,4}, h{4,3,3,4}={3,3,4,3}
3. p. 296, Table II: Regular honeycombs, δ_n+1
Kaleidoscopes: Selected Writings of H. S. M. Coxeter , editied by F. Arthur Sherk, Peter McMullen, Anthony C. Thompson, Asia Ivic Weiss, Wiley-Interscience Publication, 1995, ISBN 978-0-471-01003-6
- (Paper 24) H.S.M. Coxeter, Regular and Semi-Regular Polytopes III, [Math. Zeit. 200 (1988) 3-45]

<i>Regular Polytopes</i> (book) book about mathematical geometry

Regular Polytopes is a mathematical geometry book written by Canadian mathematician Harold Scott MacDonald Coxeter. Originally published in 1947, the book was updated and republished in 1963 and 1973.

International Standard Book Number Unique numeric book identifier

The International Standard Book Number (ISBN) is a numeric commercial book identifier which is intended to be unique. Publishers purchase ISBNs from an affiliate of the International ISBN Agency.

v t e Fundamental convex regular and uniform honeycombs in dimensions 2-9
Space	Family	${\tilde {A}}_{n-1}$	${\tilde {C}}_{n-1}$	${\tilde {B}}_{n-1}$	${\tilde {D}}_{n-1}$	${\tilde {G}}_{2}$ / ${\tilde {F}}_{4}$ / ${\tilde {E}}_{n-1}$
E²	Uniform tiling	{3^[3]}	δ₃	hδ₃	qδ₃	Hexagonal
E³	Uniform convex honeycomb	{3^[4]}	δ₄	hδ₄	qδ₄
E⁴	Uniform 4-honeycomb	{3^[5]}	δ₅	hδ₅	qδ₅	24-cell honeycomb
E⁵	Uniform 5-honeycomb	{3^[6]}	δ₆	hδ₆	qδ₆
E⁶	Uniform 6-honeycomb	{3^[7]}	δ₇	hδ₇	qδ₇	2₂₂
E⁷	Uniform 7-honeycomb	{3^[8]}	δ₈	hδ₈	qδ₈	1₃₃ • 3₃₁
E⁸	Uniform 8-honeycomb	{3^[9]}	δ₉	hδ₉	qδ₉	1₅₂ • 2₅₁ • 5₂₁
E⁹	Uniform 9-honeycomb	{3^[10]}	δ₁₀	hδ₁₀	qδ₁₀
E^n-1	Uniform (n-1)-honeycomb	{3^[n]}	δ_n	hδ_n	qδ_n	1_k2 • 2_k1 • k₂₁

This page is based on this Wikipedia article
Text is available under the CC BY-SA 4.0 license; additional terms may apply.
Images, videos and audio are available under their respective licenses.

[1] Regular and semi-regular polytopes III, p.318-319