5-cell honeycomb

4-simplex honeycomb
(No image)
Type	Uniform 4-honeycomb
Family	Simplectic honeycomb
Schläfli symbol	{3[5]} = 0[5]
Coxeter diagram
4-face types	{3,3,3} t1{3,3,3}
Cell types	{3,3} t1{3,3}
Face types	{3}
Vertex figure	t0,3{3,3,3}
Symmetry	${\displaystyle {\tilde {A}}_{4}}$×2 [3[5]]
Properties	vertex-transitive

In four-dimensional Euclidean geometry, the 4-simplex honeycomb, 5-cell honeycomb or pentachoric-dispentachoric honeycomb is a space-filling tessellation honeycomb. It is composed of 5-cells and rectified 5-cells facets in a ratio of 1:1.

Structure

Cells of the vertex figure are ten tetrahedrons and 20 triangular prisms, corresponding to the ten 5-cells and 20 rectified 5-cells that meet at each vertex. All the vertices lie in parallel realms in which they form alternated cubic honeycombs, the tetrahedra being either tops of the rectified 5-cell or the bases of the 5-cell, and the octahedra being the bottoms of the rectified 5-cell. ^[1]

Alternate names

• Cyclopentachoric tetracomb
• Pentachoric-dispentachoric tetracomb

Projection by folding

The 5-cell honeycomb can be projected into the 2-dimensional square tiling by a geometric folding operation that maps two pairs of mirrors into each other, sharing the same vertex arrangement:

${\displaystyle {\tilde {A}}_{3}}$
${\displaystyle {\tilde {C}}_{2}}$

Two different aperiodic tilings with 5-fold symmetry can be obtained by projecting two-dimensional slices of the honeycomb: the Penrose tiling composed of rhombi, and the Tübingen triangle tiling composed of isosceles triangles. ^[2]

A4 lattice

The vertex arrangement of the 5-cell honeycomb is called the A4 lattice, or 4-simplex lattice. The 20 vertices of its vertex figure, the runcinated 5-cell represent the 20 roots of the ${\displaystyle {\tilde {A}}_{4}}$ Coxeter group. ^{[3] [4]} It is the 4-dimensional case of a simplectic honeycomb.

The A^*
₄ lattice ^[5] is the union of five A₄ lattices, and is the dual to the omnitruncated 5-simplex honeycomb, and therefore the Voronoi cell of this lattice is an omnitruncated 5-cell

∪ ∪ ∪ ∪ = dual of

Related polytopes and honeycombs

The tops of the 5-cells in this honeycomb adjoin the bases of the 5-cells, and vice versa, in adjacent laminae (or layers); but alternating laminae may be inverted so that the tops of the rectified 5-cells adjoin the tops of the rectified 5-cells and the bases of the 5-cells adjoin the bases of other 5-cells. This inversion results in another non-Wythoffian uniform convex honeycomb. Octahedral prisms and tetrahedral prisms may be inserted in between alternated laminae as well, resulting in two more non-Wythoffian elongated uniform honeycombs. ^[6]

This honeycomb is one of seven unique uniform honeycombs ^[7] constructed by the ${\displaystyle {\tilde {A}}_{4}}$ Coxeter group. The symmetry can be multiplied by the symmetry of rings in the Coxeter–Dynkin diagrams:

A4 honeycombs
Pentagon symmetry	Extended symmetry	Extended diagram	Extended group	Honeycomb diagrams
a1	[3[5]]		${\displaystyle {\tilde {A}}_{4}}$	(None)
i2	[[3[5]]]		${\displaystyle {\tilde {A}}_{4}}$×2	1 ,  2 ,  3 ,   4 ,  5 ,  6
r10	[5[3[5]]]		${\displaystyle {\tilde {A}}_{4}}$×10	7

Rectified 5-cell honeycomb

Rectified 5-cell honeycomb
(No image)
Type	Uniform 4-honeycomb
Schläfli symbol	t0,2{3[5]} or r{3[5]}
Coxeter diagram
4-face types	t1{33} t0,2{33} t0,3{33}
Cell types	Tetrahedron Octahedron Cuboctahedron Triangular prism
Vertex figure	triangular elongated-antiprismatic prism
Symmetry	${\displaystyle {\tilde {A}}_{4}}$×2 [3[5]]
Properties	vertex-transitive

The rectified 4-simplex honeycomb or rectified 5-cell honeycomb is a space-filling tessellation honeycomb.

Alternate names

• small cyclorhombated pentachoric tetracomb
• small prismatodispentachoric tetracomb

Cyclotruncated 5-cell honeycomb

Cyclotruncated 5-cell honeycomb
(No image)
Type	Uniform 4-honeycomb
Family	Truncated simplectic honeycomb
Schläfli symbol	t0,1{3[5]}
Coxeter diagram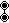
4-face types	{3,3,3} t{3,3,3} 2t{3,3,3}
Cell types	{3,3} t{3,3}
Face types	Triangle {3} Hexagon {6}
Vertex figure	Tetrahedral antiprism [3,4,2+], order 48
Symmetry	${\displaystyle {\tilde {A}}_{4}}$×2 [3[5]]
Properties	vertex-transitive

The cyclotruncated 4-simplex honeycomb or cyclotruncated 5-cell honeycomb is a space-filling tessellation honeycomb. It can also be seen as a birectified 5-cell honeycomb.

It is composed of 5-cells, truncated 5-cells, and bitruncated 5-cells facets in a ratio of 2:2:1. Its vertex figure is a tetrahedral antiprism, with 2 regular tetrahedron, 8 triangular pyramid, and 6 tetragonal disphenoid cells, defining 2 5-cell, 8 truncated 5-cell, and 6 bitruncated 5-cell facets around a vertex.

It can be constructed as five sets of parallel hyperplanes that divide space into two half-spaces. The 3-space hyperplanes contain quarter cubic honeycombs as a collection facets. ^[8]

Alternate names

• Cyclotruncated pentachoric tetracomb
• Small truncated-pentachoric tetracomb

Truncated 5-cell honeycomb

Truncated 4-simplex honeycomb
(No image)
Type	Uniform 4-honeycomb
Schläfli symbol	t0,1,2{3[5]} or t{3[5]}
Coxeter diagram
4-face types	t0,1{33} t0,1,2{33} t0,3{33}
Cell types	Tetrahedron Truncated tetrahedron Truncated octahedron Triangular prism
Vertex figure	triangular elongated-antiprismatic pyramid
Symmetry	${\displaystyle {\tilde {A}}_{4}}$×2 [3[5]]
Properties	vertex-transitive

The truncated 4-simplex honeycomb or truncated 5-cell honeycomb is a space-filling tessellation honeycomb. It can also be called a cyclocantitruncated 5-cell honeycomb.

Alaternate names

• Great cyclorhombated pentachoric tetracomb
• Great truncated-pentachoric tetracomb

Cantellated 5-cell honeycomb

Cantellated 5-cell honeycomb
(No image)
Type	Uniform 4-honeycomb
Schläfli symbol	t0,1,3{3[5]} or rr{3[5]}
Coxeter diagram
4-face types	t0,2{33} t1,2{33} t0,1,3{33}
Cell types	Truncated tetrahedron Octahedron Cuboctahedron Triangular prism Hexagonal prism
Vertex figure	Bidiminished rectified pentachoron
Symmetry	${\displaystyle {\tilde {A}}_{4}}$×2 [3[5]]
Properties	vertex-transitive

The cantellated 4-simplex honeycomb or cantellated 5-cell honeycomb is a space-filling tessellation honeycomb. It can also be called a cycloruncitruncated 5-cell honeycomb.

Alternate names

• Cycloprismatorhombated pentachoric tetracomb
• Great prismatodispentachoric tetracomb

Bitruncated 5-cell honeycomb

Bitruncated 5-cell honeycomb
(No image)
Type	Uniform 4-honeycomb
Schläfli symbol	t0,1,2,3{3[5]} or 2t{3[5]}
Coxeter diagram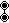
4-face types	t0,1,3{33} t0,1,2{33} t0,1,2,3{33}
Cell types	Cuboctahedron Truncated octahedron Truncated tetrahedron Hexagonal prism Triangular prism
Vertex figure	tilted rectangular duopyramid
Symmetry	${\displaystyle {\tilde {A}}_{4}}$×2 [3[5]]
Properties	vertex-transitive

The bitruncated 4-simplex honeycomb or bitruncated 5-cell honeycomb is a space-filling tessellation honeycomb. It can also be called a cycloruncicantitruncated 5-cell honeycomb.

Alternate names

• Great cycloprismated pentachoric tetracomb
• Grand prismatodispentachoric tetracomb

Omnitruncated 5-cell honeycomb

Omnitruncated 4-simplex honeycomb
(No image)
Type	Uniform 4-honeycomb
Family	Omnitruncated simplectic honeycomb
Schläfli symbol	t0,1,2,3,4{3[5]} or tr{3[5]}
Coxeter diagram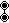
4-face types	t0,1,2,3{3,3,3}
Cell types	t0,1,2{3,3} {6}x{}
Face types	{4} {6}
Vertex figure	Irr. 5-cell
Symmetry	${\displaystyle {\tilde {A}}_{4}}$×10, [5[3[5]]]
Properties	vertex-transitive, cell-transitive

The omnitruncated 4-simplex honeycomb or omnitruncated 5-cell honeycomb is a space-filling tessellation honeycomb. It can also be seen as a cyclosteriruncicantitruncated 5-cell honeycomb.

It is composed entirely of omnitruncated 5-cell (omnitruncated 4-simplex) facets.

Coxeter calls this Hinton's honeycomb after C. H. Hinton, who described it in his book The Fourth Dimension in 1906. ^[9]

The facets of all omnitruncated simplectic honeycombs are called permutohedra and can be positioned in n+1 space with integral coordinates, permutations of the whole numbers (0,1,...,n).

Alternate names

• Omnitruncated cyclopentachoric tetracomb
• Great-prismatodecachoric tetracomb

A₄^* lattice

The A^*
₄ lattice is the union of five A₄ lattices, and is the dual to the omnitruncated 5-cell honeycomb, and therefore the Voronoi cell of this lattice is an omnitruncated 5-cell. ^[10]

∪ ∪ ∪ ∪ = dual of

Alternated form

This honeycomb can be alternated, creating omnisnub 5-cells with irregular 5-cells created at the deleted vertices. Although it is not uniform, the 5-cells have a symmetry of order 10.

See also

Regular and uniform honeycombs in 4-space:

• Tesseractic honeycomb
• 16-cell honeycomb
• 24-cell honeycomb
• Truncated 24-cell honeycomb
• Snub 24-cell honeycomb

Notes

1. Olshevsky (2006), Model 134
2. Baake, M.; Kramer, P.; Schlottmann, M.; Zeidler, D. (December 1990). "Planar Patterns with Fivefold Symmetry as Sections of Periodic Structures in 4-Space". International Journal of Modern Physics B. 04 (15n16): 2217–2268. doi:10.1142/S0217979290001054.
3. "The Lattice A4".
4. "A4 root lattice - Wolfram|Alpha".
5. "The Lattice A4".
6. Olshevsky (2006), Klitzing, elong( x3o3o3o3o3*a ) - ecypit - O141, schmo( x3o3o3o3o3*a ) - zucypit - O142, elongschmo( x3o3o3o3o3*a ) - ezucypit - O143
7. mathworld: Necklace, OEIS sequenceA000029 8-1 cases, skipping one with zero marks
8. Olshevsky, (2006) Model 135
9. The Beauty of Geometry: Twelve Essays. Dover Publications. 1999. ISBN   0-486-40919-8. LCCN   99035678. (The classification of Zonohededra, page 73)
10. The Lattice A4*

References

• Norman Johnson Uniform Polytopes, Manuscript (1991)
• Kaleidoscopes: Selected Writings of H.S.M. Coxeter, edited by F. Arthur Sherk, Peter McMullen, Anthony C. Thompson, Asia Ivic Weiss, Wiley-Interscience Publication, 1995, ISBN   978-0-471-01003-6
  • (Paper 22) H.S.M. Coxeter, Regular and Semi Regular Polytopes I, [Math. Zeit. 46 (1940) 380–407, MR 2,10] (1.9 Uniform space-fillings)
  • (Paper 24) H.S.M. Coxeter, Regular and Semi-Regular Polytopes III, [Math. Zeit. 200 (1988) 3-45]
• George Olshevsky, Uniform Panoploid Tetracombs, Manuscript (2006) (Complete list of 11 convex uniform tilings, 28 convex uniform honeycombs, and 143 convex uniform tetracombs) Model 134
• Klitzing, Richard. "4D Euclidean tesselations"., x3o3o3o3o3*a - cypit - O134, x3x3x3x3x3*a - otcypit - 135, x3x3x3o3o3*a - gocyropit - O137, x3x3o3x3o3*a - cypropit - O138, x3x3x3x3o3*a - gocypapit - O139, x3x3x3x3x3*a - otcypit - 140
• Affine Coxeter group Wa(A4), Quaternions, and Decagonal Quasicrystals, Mehmet Koca, Nazife O. Koca, Ramazan Koc (2013) arXiv : 1209.1878

v t e Fundamental convex regular and uniform honeycombs in dimensions 2–9
Space	Family	${\displaystyle {\tilde {A}}_{n-1}}$	${\displaystyle {\tilde {C}}_{n-1}}$	${\displaystyle {\tilde {B}}_{n-1}}$	${\displaystyle {\tilde {D}}_{n-1}}$	${\displaystyle {\tilde {G}}_{2}}$ / ${\displaystyle {\tilde {F}}_{4}}$ / ${\displaystyle {\tilde {E}}_{n-1}}$
E2	Uniform tiling	0[3]	δ3	hδ3	qδ3	Hexagonal
E3	Uniform convex honeycomb	0[4]	δ4	hδ4	qδ4
E4	Uniform 4-honeycomb	0[5]	δ5	hδ5	qδ5	24-cell honeycomb
E5	Uniform 5-honeycomb	0[6]	δ6	hδ6	qδ6
E6	Uniform 6-honeycomb	0[7]	δ7	hδ7	qδ7	222
E7	Uniform 7-honeycomb	0[8]	δ8	hδ8	qδ8	133 • 331
E8	Uniform 8-honeycomb	0[9]	δ9	hδ9	qδ9	152 • 251 • 521
E9	Uniform 9-honeycomb	0[10]	δ10	hδ10	qδ10
E10	Uniform 10-honeycomb	0[11]	δ11	hδ11	qδ11
En−1	Uniform (n−1)-honeycomb	0[n]	δn	hδn	qδn	1k2 • 2k1 • k21