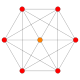
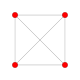
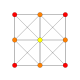
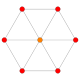
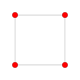
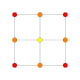
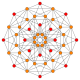
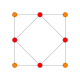
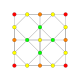
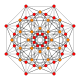
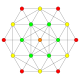
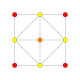
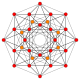
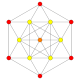
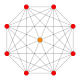
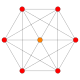
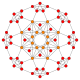
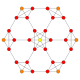
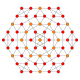
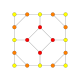
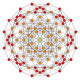
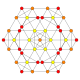
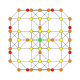
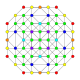
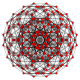
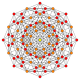
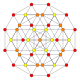
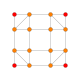
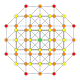
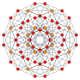
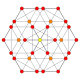
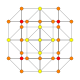
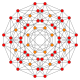
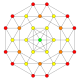
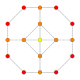
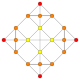
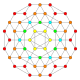
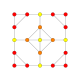
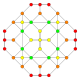
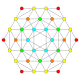
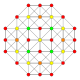
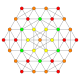
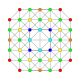
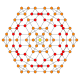
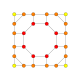
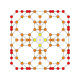
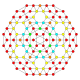
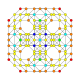
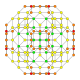
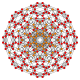
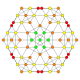
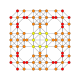
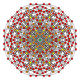
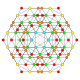
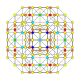
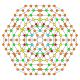
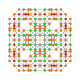
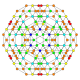
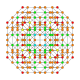
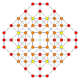
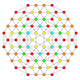
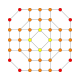
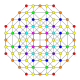
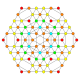
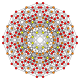
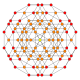
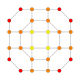
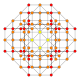
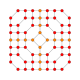
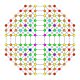
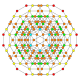
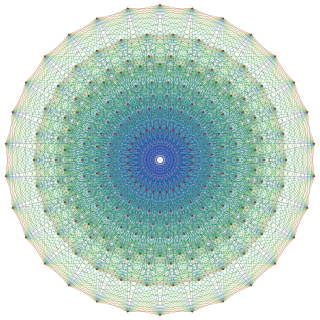
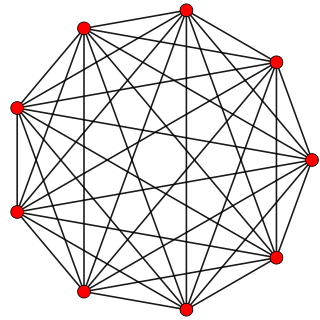
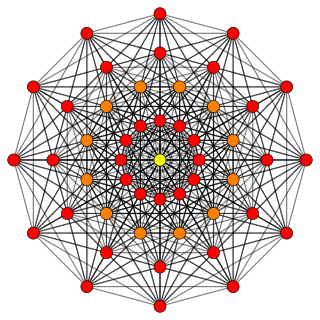
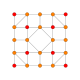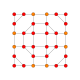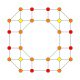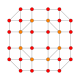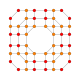B5 polytope

Last updated March 12, 2019

Orthographic projections in the B₅ Coxeter plane
5-cube	5-orthoplex	5-demicube

In 5-dimensional geometry, there are 31 uniform polytopes with B₅ symmetry. There are two regular forms, the 5-orthoplex, and 5-cube with 10 and 32 vertices respectively. The 5-demicube is added as an alternation of the 5-cube.

Geometry is a branch of mathematics concerned with questions of shape, size, relative position of figures, and the properties of space. A mathematician who works in the field of geometry is called a geometer.

In geometry, a uniform 5-polytope is a five-dimensional uniform polytope. By definition, a uniform 5-polytope is vertex-transitive and constructed from uniform 4-polytope facets.

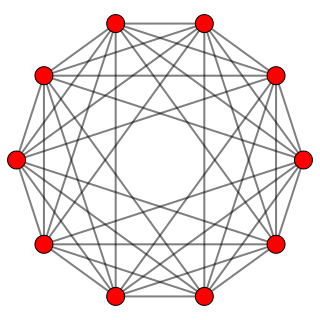
In five-dimensional geometry, a 5-orthoplex, or 5-cross polytope, is a five-dimensional polytope with 10 vertices, 40 edges, 80 triangle faces, 80 tetrahedron cells, 32 5-cell 4-faces.

Orthographic projection is a means of representing three-dimensional objects in two dimensions. It is a form of parallel projection, in which all the projection lines are orthogonal to the projection plane, resulting in every plane of the scene appearing in affine transformation on the viewing surface. The obverse of an orthographic projection is an oblique projection, which is a parallel projection in which the projection lines are not orthogonal to the projection plane.

Graphs

Symmetric orthographic projections of these 32 polytopes can be made in the B₅, B₄, B₃, B₂, A₃, Coxeter planes. A_k has [k+1] symmetry, and B_k has [2k] symmetry.

These 32 polytopes are each shown in these 5 symmetry planes, with vertices and edges drawn, and vertices colored by the number of overlapping vertices in each projective position.

#	Graph B₅ / A₄ [10]	Graph B₄ / D₅ [8]	Graph B₃ / A₂ [6]	Graph B₂ [4]	Graph A₃ [4]	Coxeter-Dynkin diagram and Schläfli symbol Johnson and Bowers names
1						h{4,3,3,3} 5-demicube Hemipenteract (hin)
2						{4,3,3,3} 5-cube Penteract (pent)
3						t₁{4,3,3,3} = r{4,3,3,3} Rectified 5-cube Rectified penteract (rin)
4						t₂{4,3,3,3} = 2r{4,3,3,3} Birectified 5-cube Penteractitriacontiditeron (nit)
5						t₁{3,3,3,4} = r{3,3,3,4} Rectified 5-orthoplex Rectified triacontiditeron (rat)
6						{3,3,3,4} 5-orthoplex Triacontiditeron (tac)
7						t_0,1{4,3,3,3} = t{3,3,3,4} Truncated 5-cube Truncated penteract (tan)
8						t_1,2{4,3,3,3} = 2t{4,3,3,3} Bitruncated 5-cube Bitruncated penteract (bittin)
9						t_0,2{4,3,3,3} = rr{4,3,3,3} Cantellated 5-cube Rhombated penteract (sirn)
10						t_1,3{4,3,3,3} = 2rr{4,3,3,3} Bicantellated 5-cube Small birhombi-penteractitriacontiditeron (sibrant)
11						t_0,3{4,3,3,3} Runcinated 5-cube Prismated penteract (span)
12						t_0,4{4,3,3,3} = 2r2r{4,3,3,3} Stericated 5-cube Small celli-penteractitriacontiditeron (scant)
13						t_0,1{3,3,3,4} = t{3,3,3,4} Truncated 5-orthoplex Truncated triacontiditeron (tot)
14						t_1,2{3,3,3,4} = 2t{3,3,3,4} Bitruncated 5-orthoplex Bitruncated triacontiditeron (bittit)
15						t_0,2{3,3,3,4} = rr{3,3,3,4} Cantellated 5-orthoplex Small rhombated triacontiditeron (sart)
16						t_0,3{3,3,3,4} Runcinated 5-orthoplex Small prismated triacontiditeron (spat)
17						t_0,1,2{4,3,3,3} = tr{4,3,3,3} Cantitruncated 5-cube Great rhombated penteract (girn)
18						t_1,2,3{4,3,3,3} = tr{4,3,3,3} Bicantitruncated 5-cube Great birhombi-penteractitriacontiditeron (gibrant)
19						t_0,1,3{4,3,3,3} Runcitruncated 5-cube Prismatotruncated penteract (pattin)
20						t_0,2,3{4,3,3,3} Runcicantellated 5-cube Prismatorhomated penteract (prin)
21						t_0,1,4{4,3,3,3} Steritruncated 5-cube Cellitruncated penteract (capt)
22						t_0,2,4{4,3,3,3} Stericantellated 5-cube Cellirhombi-penteractitriacontiditeron (carnit)
23						t_0,1,2,3{4,3,3,3} Runcicantitruncated 5-cube Great primated penteract (gippin)
24						t_0,1,2,4{4,3,3,3} Stericantitruncated 5-cube Celligreatorhombated penteract (cogrin)
25						t_0,1,3,4{4,3,3,3} Steriruncitruncated 5-cube Celliprismatotrunki-penteractitriacontiditeron (captint)
26						t_0,1,2,3,4{4,3,3,3} Omnitruncated 5-cube Great celli-penteractitriacontiditeron (gacnet)
27						t_0,1,2{3,3,3,4} = tr{3,3,3,4} Cantitruncated 5-orthoplex Great rhombated triacontiditeron (gart)
28						t_0,1,3{3,3,3,4} Runcitruncated 5-orthoplex Prismatotruncated triacontiditeron (pattit)
29						t_0,2,3{3,3,3,4} Runcicantellated 5-orthoplex Prismatorhombated triacontiditeron (pirt)
30						t_0,1,4{3,3,3,4} Steritruncated 5-orthoplex Cellitruncated triacontiditeron (cappin)
31						t_0,1,2,3{3,3,3,4} Runcicantitruncated 5-orthoplex Great prismatorhombated triacontiditeron (gippit)
32						t_0,1,2,4{3,3,3,4} Stericantitruncated 5-orthoplex Celligreatorhombated triacontiditeron (cogart)

Related Research Articles

In 8-dimensional geometry, there are 255 uniform polytopes with E₈ symmetry. The three simplest forms are the 4₂₁, 2₄₁, and 1₄₂ polytopes, composed of 240, 2160 and 17280 vertices respectively.

In 7-dimensional geometry, there are 127 uniform polytopes with E₇ symmetry. The three simplest forms are the 3₂₁, 2₃₁, and 1₃₂ polytopes, composed of 56, 126, and 576 vertices respectively.

In 6-dimensional geometry, there are 39 uniform polytopes with E₆ symmetry. The two simplest forms are the 2₂₁ and 1₂₂ polytopes, composed of 27 and 72 vertices respectively.

In geometry of five dimensions or higher, a cantic 5-cube, cantihalf 5-cube, truncated 5-demicube is a uniform 5-polytope, being a truncation of the 5-demicube. It has half the vertices of a cantellated 5-cube.

In eight-dimensional geometry, a pentellated 8-simplex is a convex uniform 8-polytope with 5th order truncations of the regular 8-simplex.

In 8-dimensional geometry, there are 135 uniform polytopes with A₈ symmetry. There is one self-dual regular form, the 8-simplex with 9 vertices.

In 7-dimensional geometry, there are 128 uniform polytopes with B₇ symmetry. There are two regular forms, the 7-orthoplex, and 8-cube with 14 and 128 vertices respectively. The 7-demicube is added with half of the symmetry.

In 7-dimensional geometry, there are 71 uniform polytopes with A₇ symmetry. There is one self-dual regular form, the 7-simplex with 8 vertices.

In 6-dimensional geometry, there are 35 uniform polytopes with A₆ symmetry. There is one self-dual regular form, the 6-simplex with 7 vertices.

In 6-dimensional geometry, there are 64 uniform polytopes with B₆ symmetry. There are two regular forms, the 6-orthoplex, and 6-cube with 12 and 64 vertices respectively. The 6-demicube is added with half the symmetry.

In 6-dimensional geometry, there are 47 uniform polytopes with D₆ symmetry, 16 are unique, and 31 are shared with the B₆ symmetry. There are two regular forms, the 6-orthoplex, and 6-demicube with 12 and 32 vertices respectively.

In 7-dimensional geometry, there are 95 uniform polytopes with D₇ symmetry; 32 are unique, and 63 are shared with the B₇ symmetry. There are two regular forms, the 7-orthoplex, and 7-demicube with 14 and 64 vertices respectively.

In 5-dimensional geometry, there are 19 uniform polytopes with A₅ symmetry. There is one self-dual regular form, the 5-simplex with 6 vertices.

In 5-dimensional geometry, there are 23 uniform polytopes with D₅ symmetry, 8 are unique, and 15 are shared with the B₅ symmetry. There are two special forms, the 5-orthoplex, and 5-demicube with 10 and 16 vertices respectively.

In six-dimensional geometry, a runcic 5-cube or is a convex uniform 5-polytope. There are 2 runcic forms for the 5-cube. Runcic 5-cubes have half the vertices of runcinated 5-cubes.

In seven-dimensional geometry, a cantic 7-cube or truncated 7-demicube as a uniform 7-polytope, being a truncation of the 7-demicube.

In 4-dimensional geometry, there are 9 uniform polytopes with A₄ symmetry. There is one self-dual regular form, the 5-cell with 5 vertices.

In 4-dimensional geometry, there are 15 uniform 4-polytopes with B₄ symmetry. There are two regular forms, the tesseract, and 16-cell with 16 and 8 vertices respectively.

In 4-dimensional geometry, there are 7 uniform 4-polytopes with reflections of D₄ symmetry, all are shared with higher symmetry constructions in the B₄ or F₄ symmetry families. there is also one half symmetry alternation, the snub 24-cell.

References

H.S.M. Coxeter:
- H.S.M. Coxeter, Regular Polytopes, 3rd Edition, Dover New York, 1973
Kaleidoscopes: Selected Writings of H.S.M. Coxeter, edited by F. Arthur Sherk, Peter McMullen, Anthony C. Thompson, Asia Ivic Weiss, Wiley-Interscience Publication, 1995, ISBN 978-0-471-01003-6 ^[1]
- (Paper 22) H.S.M. Coxeter, Regular and Semi Regular Polytopes I, [Math. Zeit. 46 (1940) 380-407, MR 2,10]
- (Paper 23) H.S.M. Coxeter, Regular and Semi-Regular Polytopes II, [Math. Zeit. 188 (1985) 559-591]
- (Paper 24) H.S.M. Coxeter, Regular and Semi-Regular Polytopes III, [Math. Zeit. 200 (1988) 3-45]
N.W. Johnson: The Theory of Uniform Polytopes and Honeycombs, Ph.D. Dissertation, University of Toronto, 1966

Harold Scott MacDonald Coxeter Canadian mathematician

Harold Scott MacDonald "Donald" Coxeter, FRS, FRSC, was a British-born Canadian geometer. Coxeter is regarded as one of the greatest geometers of the 20th century. He was born in London, received his BA (1929) and PhD (1931) from Cambridge, but lived in Canada from age 29. He was always called Donald, from his third name MacDonald. He was most noted for his work on regular polytopes and higher-dimensional geometries. He was a champion of the classical approach to geometry, in a period when the tendency was to approach geometry more and more via algebra.

International Standard Book Number Unique numeric book identifier

The International Standard Book Number (ISBN) is a numeric commercial book identifier which is intended to be unique. Publishers purchase ISBNs from an affiliate of the International ISBN Agency.

External links

Klitzing, Richard. "5D uniform polytopes (polytera)".

Notes

↑ Wiley::Kaleidoscopes: Selected Writings of H.S.M. Coxeter

v t e Fundamental convex regular and uniform polytopes in dimensions 2–10
Family	A_n	B_n	I₂(p) / D_n	E₆ / E₇ / E₈ / F₄ / G₂	H_n
Regular polygon	Triangle	Square	p-gon	Hexagon	Pentagon
Uniform polyhedron	Tetrahedron	Octahedron • Cube	Demicube		Dodecahedron • Icosahedron
Uniform 4-polytope	5-cell	16-cell • Tesseract	Demitesseract	24-cell	120-cell • 600-cell
Uniform 5-polytope	5-simplex	5-orthoplex • 5-cube	5-demicube
Uniform 6-polytope	6-simplex	6-orthoplex • 6-cube	6-demicube	1₂₂ • 2₂₁
Uniform 7-polytope	7-simplex	7-orthoplex • 7-cube	7-demicube	1₃₂ • 2₃₁ • 3₂₁
Uniform 8-polytope	8-simplex	8-orthoplex • 8-cube	8-demicube	1₄₂ • 2₄₁ • 4₂₁
Uniform 9-polytope	9-simplex	9-orthoplex • 9-cube	9-demicube
Uniform 10-polytope	10-simplex	10-orthoplex • 10-cube	10-demicube
Uniform n-polytope	n-simplex	n-orthoplex • n-cube	n-demicube	1_k2 • 2_k1 • k₂₁	n-pentagonal polytope
Topics: Polytope families • Regular polytope • List of regular polytopes and compounds

This page is based on this Wikipedia article
Text is available under the CC BY-SA 4.0 license; additional terms may apply.
Images, videos and audio are available under their respective licenses.

[1] Wiley::Kaleidoscopes: Selected Writings of H.S.M. Coxeter