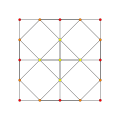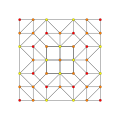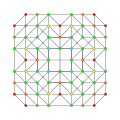A5 polytope

Orthographic projections
A₅ Coxeter plane

5-simplex

In 5-dimensional geometry, there are 19 uniform polytopes with A₅ symmetry. There is one self-dual regular form, the 5-simplex with 6 vertices.

Each can be visualized as symmetric orthographic projections in the Coxeter planes of the A₅ Coxeter group and other subgroups.

Graphs

Symmetric orthographic projections of these 19 polytopes can be made in the A₅, A₄, A₃, A₂ Coxeter planes. A_k graphs have [k+1] symmetry. For even k and symmetrically nodea_1ed-diagrams, symmetry doubles to [2(k+1)].

These 19 polytopes are each shown in these 4 symmetry planes, with vertices and edges drawn and vertices colored by the number of overlapping vertices in each projective position.

#	Coxeter plane graphs				Coxeter-Dynkin diagram Schläfli symbol Name
	[6]	[5]	[4]	[3]
	A5	A4	A3	A2
1					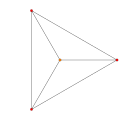{3,3,3,3} 5-simplex (hix)
2					t1{3,3,3,3} or r{3,3,3,3} Rectified 5-simplex (rix)
3				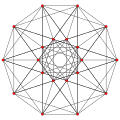	t2{3,3,3,3} or 2r{3,3,3,3} Birectified 5-simplex (dot)
4					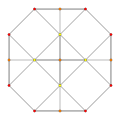t0,1{3,3,3,3} or t{3,3,3,3} Truncated 5-simplex (tix)
5				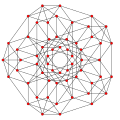	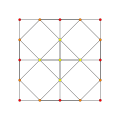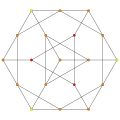t1,2{3,3,3,3} or 2t{3,3,3,3} Bitruncated 5-simplex (bittix)
6					t0,2{3,3,3,3} or rr{3,3,3,3} Cantellated 5-simplex (sarx)
7					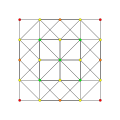t1,3{3,3,3,3} or 2rr{3,3,3,3} Bicantellated 5-simplex (sibrid)
8		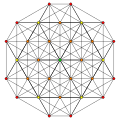			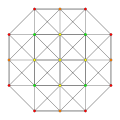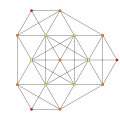t0,3{3,3,3,3} Runcinated 5-simplex (spix)
9		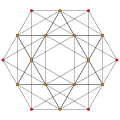			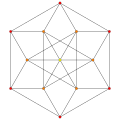t0,4{3,3,3,3} or 2r2r{3,3,3,3} Stericated 5-simplex (scad)
10					t0,1,2{3,3,3,3} or tr{3,3,3,3} Cantitruncated 5-simplex (garx)
11		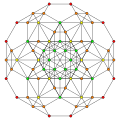			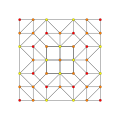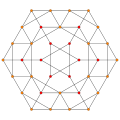t1,2,3{3,3,3,3} or 2tr{3,3,3,3} Bicantitruncated 5-simplex (gibrid)
12					t0,1,3{3,3,3,3} Runcitruncated 5-simplex (pattix)
13		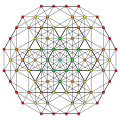			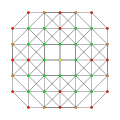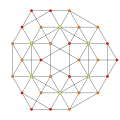t0,2,3{3,3,3,3} Runcicantellated 5-simplex (pirx)
14					t0,1,4{3,3,3,3} Steritruncated 5-simplex (cappix)
15					t0,2,4{3,3,3,3} Stericantellated 5-simplex (card)
16		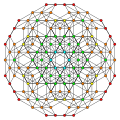			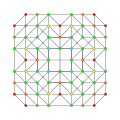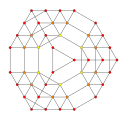t0,1,2,3{3,3,3,3} Runcicantitruncated 5-simplex (gippix)
17					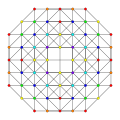t0,1,2,4{3,3,3,3} Stericantitruncated 5-simplex (cograx)
18					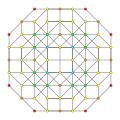t0,1,3,4{3,3,3,3} Steriruncitruncated 5-simplex (captid)
19					t0,1,2,3,4{3,3,3,3} Omnitruncated 5-simplex (gocad)

A5 polytopes
t0	t1	t2	t0,1	t0,2	t1,2	t0,3
t1,3	t0,4	t0,1,2	t0,1,3	t0,2,3	t1,2,3	t0,1,4
t0,2,4	t0,1,2,3	t0,1,2,4	t0,1,3,4	t0,1,2,3,4

References

• H.S.M. Coxeter:
  • H.S.M. Coxeter, Regular Polytopes, 3rd Edition, Dover, New York, 1973
• Kaleidoscopes: Selected Writings of H.S.M. Coxeter, edited by F. Arthur Sherk, Peter McMullen, Anthony C. Thompson, and Asia Ivic Weiss, Wiley-Interscience Publication, 1995, ISBN   978-0-471-01003-6 ^[1]
  • (Paper 22) H.S.M. Coxeter, Regular and Semi Regular Polytopes I, [Math. Zeit. 46 (1940) 380–407, MR 2, 10]
  • (Paper 23) H.S.M. Coxeter, Regular and Semi-Regular Polytopes II, [Math. Zeit. 188 (1985) 559-591]
  • (Paper 24) H.S.M. Coxeter, Regular and Semi-Regular Polytopes III, [Math. Zeit. 200 (1988) 3-45]
• N.W. Johnson: The Theory of Uniform Polytopes and Honeycombs, Ph.D. Dissertation, University of Toronto, 1966

External links

• Klitzing, Richard. "5D uniform polytopes (polytera)".

Notes

1. "Wiley::Kaleidoscopes: Selected Writings of H.S.M. Coxeter". Archived from the original on 2016-07-11. Retrieved 2011-03-30.

v t e Fundamental convex regular and uniform polytopes in dimensions 2–10
Family	An	Bn	I2(p) / Dn	E6 / E7 / E8 / F4 / G2	Hn
Regular polygon	Triangle	Square	p-gon	Hexagon	Pentagon
Uniform polyhedron	Tetrahedron	Octahedron • Cube	Demicube		Dodecahedron • Icosahedron
Uniform polychoron	Pentachoron	16-cell • Tesseract	Demitesseract	24-cell	120-cell • 600-cell
Uniform 5-polytope	5-simplex	5-orthoplex • 5-cube	5-demicube
Uniform 6-polytope	6-simplex	6-orthoplex • 6-cube	6-demicube	122 • 221
Uniform 7-polytope	7-simplex	7-orthoplex • 7-cube	7-demicube	132 • 231 • 321
Uniform 8-polytope	8-simplex	8-orthoplex • 8-cube	8-demicube	142 • 241 • 421
Uniform 9-polytope	9-simplex	9-orthoplex • 9-cube	9-demicube
Uniform 10-polytope	10-simplex	10-orthoplex • 10-cube	10-demicube
Uniform n-polytope	n-simplex	n-orthoplex • n-cube	n-demicube	1k2 • 2k1 • k21	n-pentagonal polytope
Topics: Polytope families • Regular polytope • List of regular polytopes and compounds • Polytope operations