In geometry, a 4-polytope is a four-dimensional polytope. It is a connected and closed figure, composed of lower-dimensional polytopal elements: vertices, edges, faces (polygons), and cells (polyhedra). Each face is shared by exactly two cells. The 4-polytopes were discovered by the Swiss mathematician Ludwig Schläfli before 1853.

In geometry, a uniform 4-polytope is a 4-dimensional polytope which is vertex-transitive and whose cells are uniform polyhedra, and faces are regular polygons.

In hyperbolic geometry, the order-4 dodecahedral honeycomb is one of four compact regular space-filling tessellations of hyperbolic 3-space. With Schläfli symbol {5,3,4}, it has four dodecahedra around each edge, and 8 dodecahedra around each vertex in an octahedral arrangement. Its vertices are constructed from 3 orthogonal axes. Its dual is the order-5 cubic honeycomb.

In hyperbolic geometry, the order-5 cubic honeycomb is one of four compact regular space-filling tessellations in hyperbolic 3-space. With Schläfli symbol {4,3,5}, it has five cubes {4,3} around each edge, and 20 cubes around each vertex. It is dual with the order-4 dodecahedral honeycomb.

In geometry, the icosahedral honeycomb is one of four compact, regular, space-filling tessellations in hyperbolic 3-space. With Schläfli symbol {3,5,3}, there are three icosahedra around each edge, and 12 icosahedra around each vertex, in a regular dodecahedral vertex figure.

In four-dimensional geometry, a cantellated 5-cell is a convex uniform 4-polytope, being a cantellation of the regular 5-cell.

In four-dimensional geometry, a cantellated 120-cell is a convex uniform 4-polytope, being a cantellation of the regular 120-cell.

In four-dimensional geometry, a runcinated 120-cell is a convex uniform 4-polytope, being a runcination of the regular 120-cell.

In geometry, a uniform polytope of dimension three or higher is a vertex-transitive polytope bounded by uniform facets. The uniform polytopes in two dimensions are the regular polygons.

In geometry, a truncated tetrahedral prism is a convex uniform polychoron. This polychoron has 10 polyhedral cells: 2 truncated tetrahedra connected by 4 triangular prisms and 4 hexagonal prisms. It has 24 faces: 8 triangular, 18 square, and 8 hexagons. It has 48 edges and 24 vertices.
In 4-dimensional geometry, a truncated octahedral prism or omnitruncated tetrahedral prism is a convex uniform 4-polytope. This 4-polytope has 16 cells It has 64 faces, and 96 edges and 48 vertices.

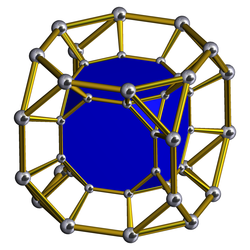
In geometry, a truncated dodecahedral prism is a convex uniform polychoron.

In geometry, a rhombicosidodecahedral prism or small rhombicosidodecahedral prism is a convex uniform polychoron.
In geometry, a rhombicuboctahedral prism is a convex uniform polychoron.

In geometry, a truncated cuboctahedral prism or great rhombicuboctahedral prism is a convex uniform polychoron.
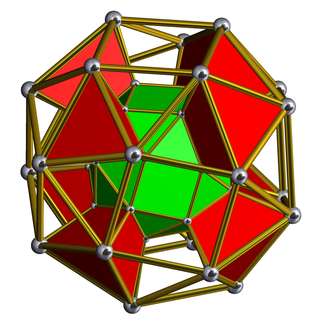
In geometry, a snub cubic prism or snub cuboctahedral prism is a convex uniform polychoron.

In geometry, a truncated icosahedral prism is a convex uniform polychoron.

In geometry, a truncated icosidodecahedral prism or great rhombicosidodecahedral prism is a convex uniform 4-polytope.

The order-6 cubic honeycomb is a paracompact regular space-filling tessellation in hyperbolic 3-space. It is paracompact because it has vertex figures composed of an infinite number of facets, with all vertices as ideal points at infinity. With Schläfli symbol {4,3,6}, the honeycomb has six ideal cubes meeting along each edge. Its vertex figure is an infinite triangular tiling. Its dual is the order-4 hexagonal tiling honeycomb.