Chaim Goodman-Strauss (born June 22, 1967 in Austin, Texas) is an American mathematician who works in convex geometry, especially aperiodic tiling. He retired from the faculty of the University of Arkansas and currently serves as outreach mathematician for the National Museum of Mathematics. He is co-author with John H. Conway and Heidi Burgiel of The Symmetries of Things , a comprehensive book surveying the mathematical theory of patterns. [1]
Goodman-Strauss received both his B.S. (1988) and Ph.D. (1994) in mathematics from the University of Texas at Austin. [2] His doctoral advisor was John Edwin Luecke. [3] He joined the faculty at the University of Arkansas, Fayetteville (UA) in 1994 and served as departmental chair from 2008 to 2015. He held visiting positions at the National Autonomous University of Mexico and Princeton University. [2] [4]
During 1995 he did research at The Geometry Center, a mathematics research and education center at the University of Minnesota, where he investigated aperiodic tilings of the plane. [5]
Goodman-Strauss has been fascinated by patterns and mathematical paradoxes for as long as he can remember. He attended a lecture about the mathematician Georg Cantor when he was 17 and says, "I was already doomed to be a mathematician, but that lecture sealed my fate." [6] He became a mathematics writer and popularizer. From 2004 to 2012, in conjunction with KUAF 91.3 FM, the University of Arkansas NPR affiliate, he presented "The Math Factor," a podcast website dealing with recreational mathematics. [7] He is an admirer of Martin Gardner and is on the advisory council of Gathering 4 Gardner, an organization that celebrates the legacy of the famed mathematics popularizer and Scientific American columnist, [8] and is active in the associated Celebration of Mind events. [9] [10] In 2022 Goodman-Strauss was awarded the National Museum of Mathematics' Rosenthal Prize, which recognizes innovation and inspiration in math teaching. [11]
On Mar 20, 2023 Strauss, together with David Smith, Joseph Samuel Myers and Craig S. Kaplan, announced the proof that the tile discovered by David Smith is an aperiodic monotile, [12] i.e., a solution to a longstanding open einstein problem. [13] The team continues to refine this work. [14]
In 2008 Goodman-Strauss teamed up with J. H. Conway and Heidi Burgiel to write The Symmetries of Things , an exhaustive and reader-accessible overview of the mathematical theory of patterns. He produced hundreds of full-color images for this book using software that he developed for the purpose. [15] The Mathematical Association of America said, "The first thing one notices when one picks up a copy … is that it is a beautiful book … filled with gorgeous color pictures … many of which were generated by Goodman-Strauss. Unlike some books which add in illustrations to keep the reader's attention, the pictures are genuinely essential to the topic of this book." [16]
He also creates large-scale sculptures inspired by mathematics, and some of these have been featured at Gathering 4 Gardner conferences. [17]
In mathematics, a prototile is one of the shapes of a tile in a tessellation.
A tessellation or tiling is the covering of a surface, often a plane, using one or more geometric shapes, called tiles, with no overlaps and no gaps. In mathematics, tessellation can be generalized to higher dimensions and a variety of geometries.
An aperiodic tiling is a non-periodic tiling with the additional property that it does not contain arbitrarily large periodic regions or patches. A set of tile-types is aperiodic if copies of these tiles can form only non-periodic tilings.
In geometry, the truncated hexagonal tiling is a semiregular tiling of the Euclidean plane. There are 2 dodecagons (12-sides) and one triangle on each vertex.
In geometry, the truncated square tiling is a semiregular tiling by regular polygons of the Euclidean plane with one square and two octagons on each vertex. This is the only edge-to-edge tiling by regular convex polygons which contains an octagon. It has Schläfli symbol of t{4,4}.
In geometry, the snub hexagonal tiling is a semiregular tiling of the Euclidean plane. There are four triangles and one hexagon on each vertex. It has Schläfli symbol sr{3,6}. The snub tetrahexagonal tiling is a related hyperbolic tiling with Schläfli symbol sr{4,6}.
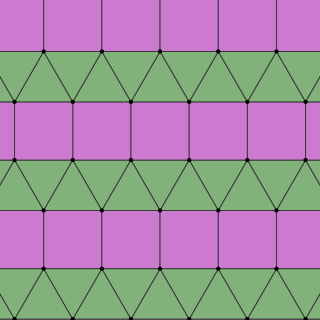
In geometry, the elongated triangular tiling is a semiregular tiling of the Euclidean plane. There are three triangles and two squares on each vertex. It is named as a triangular tiling elongated by rows of squares, and given Schläfli symbol {3,6}:e.
In geometry, the tetrapentagonal tiling is a uniform tiling of the hyperbolic plane. It has Schläfli symbol of t1{4,5} or r{4,5}.
In geometry, the snub octaoctagonal tiling is a uniform tiling of the hyperbolic plane. It has Schläfli symbol of sr{8,8}.
In geometry, the truncated order-3 apeirogonal tiling is a uniform tiling of the hyperbolic plane with a Schläfli symbol of t{∞,3}.
In geometry, the truncated infinite-order triangular tiling is a uniform tiling of the hyperbolic plane with a Schläfli symbol of t{3,∞}.
In geometry, the truncated triapeirogonal tiling is a uniform tiling of the hyperbolic plane with a Schläfli symbol of tr{∞,3}.
In geometry, the snub triapeirogonal tiling is a uniform tiling of the hyperbolic plane with a Schläfli symbol of sr{∞,3}.
In geometry, the infinite-order square tiling is a regular tiling of the hyperbolic plane. It has Schläfli symbol of {4,∞}. All vertices are ideal, located at "infinity", seen on the boundary of the Poincaré hyperbolic disk projection.
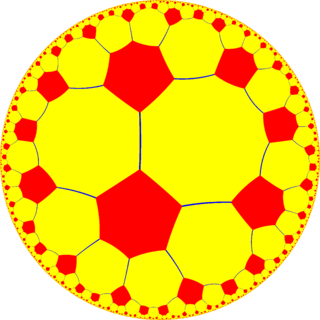
In geometry, the truncated order-6 pentagonal tiling is a uniform tiling of the hyperbolic plane. It has Schläfli symbol of t1,2{6,5}.
In geometry, the quarter order-6 square tiling is a uniform tiling of the hyperbolic plane. It has Schläfli symbol of q{4,6}. It is constructed from *3232 orbifold notation, and can be seen as a half symmetry of *443 and *662, and quarter symmetry of *642.
In plane geometry, the einstein problem asks about the existence of a single prototile that by itself forms an aperiodic set of prototiles; that is, a shape that can tessellate space but only in a nonperiodic way. Such a shape is called an einstein, a word play on ein Stein, German for "one stone".
Craig S. Kaplan is a Canadian computer scientist, mathematician, and mathematical artist. He is an editor of the Journal of Mathematics and the Arts, and an organizer of the Bridges Conference on mathematics and art. He is an associate professor of computer science at the University of Waterloo, Canada.
David Smith is an amateur mathematician and retired print technician from Bridlington, England, who is best known for his discoveries related to aperiodic monotiles that helped to solve the einstein problem.
| International | |
|---|---|
| National | |
| Academics | |
| Other | |
