Day convolution

Last updated January 29, 2025

In mathematics, specifically in category theory, Day convolution is an operation on functors that can be seen as a categorified version of function convolution. It was first introduced by Brian Day in 1970^[1] in the general context of enriched functor categories.

Definition

First version

Given $F,G\colon \mathbf {C} \to \mathbf {D}$ for two symmetric monoidal $\mathbf {C} ,\mathbf {D}$ , we define their Day convolution as follows.

It is the left kan extension along $\mathbf {C} \times \mathbf {C} \to ^{\otimes }\mathbf {C}$ of the composition $\mathbf {C} \times \mathbf {C} \to ^{F,G}\mathbf {D} \times \mathbf {D} \to ^{\otimes }\mathbf {D}$

Thus evaluated on an object $O\in \mathbf {C}$ , intuitively we get a colimit in $\mathbf {D}$ of $F(x)\otimes G(y)$ along approximations of $O\in \mathbf {C}$ as a pure tensor $x\otimes y$

Left kan extensions are computed via coends, which leads to the version below.

Enriched version

Let $(\mathbf {C} ,\otimes _{c})$ be a monoidal category enriched over a symmetric monoidal closed category $(V,\otimes )$ . Given two functors $F,G\colon \mathbf {C} \to V$ , we define their Day convolution as the following coend.^[2]

F\otimes _{d}G=\int ^{x,y\in \mathbf {C} }\mathbf {C} (x\otimes _{c}y,-)\otimes Fx\otimes Gy

If $\otimes _{c}$ is symmetric, then $\otimes _{d}$ is also symmetric. We can show this defines an associative monoidal product:

{\begin{aligned}&(F\otimes _{d}G)\otimes _{d}H\\[5pt]\cong {}&\int ^{c_{1},c_{2}}(F\otimes _{d}G)c_{1}\otimes Hc_{2}\otimes \mathbf {C} (c_{1}\otimes _{c}c_{2},-)\\[5pt]\cong {}&\int ^{c_{1},c_{2}}\left(\int ^{c_{3},c_{4}}Fc_{3}\otimes Gc_{4}\otimes \mathbf {C} (c_{3}\otimes _{c}c_{4},c_{1})\right)\otimes Hc_{2}\otimes \mathbf {C} (c_{1}\otimes _{c}c_{2},-)\\[5pt]\cong {}&\int ^{c_{1},c_{2},c_{3},c_{4}}Fc_{3}\otimes Gc_{4}\otimes Hc_{2}\otimes \mathbf {C} (c_{3}\otimes _{c}c_{4},c_{1})\otimes \mathbf {C} (c_{1}\otimes _{c}c_{2},-)\\[5pt]\cong {}&\int ^{c_{1},c_{2},c_{3},c_{4}}Fc_{3}\otimes Gc_{4}\otimes Hc_{2}\otimes \mathbf {C} (c_{3}\otimes _{c}c_{4}\otimes _{c}c_{2},-)\\[5pt]\cong {}&\int ^{c_{1},c_{2},c_{3},c_{4}}Fc_{3}\otimes Gc_{4}\otimes Hc_{2}\otimes \mathbf {C} (c_{2}\otimes _{c}c_{4},c_{1})\otimes \mathbf {C} (c_{3}\otimes _{c}c_{1},-)\\[5pt]\cong {}&\int ^{c_{1},c_{3}}Fc_{3}\otimes (G\otimes _{d}H)c_{1}\otimes \mathbf {C} (c_{3}\otimes _{c}c_{1},-)\\[5pt]\cong {}&F\otimes _{d}(G\otimes _{d}H)\end{aligned}}

Related Research Articles

In mathematics, the tensor product $of two vector spaces V and W is a vector space to which is associated a bilinear map that maps a pair to an element of denoted ⁠ ⁠ .$

In mathematics, the Yoneda lemma is a fundamental result in category theory. It is an abstract result on functors of the type morphisms into a fixed object. It is a vast generalisation of Cayley's theorem from group theory. It allows the embedding of any locally small category into a category of functors defined on that category. It also clarifies how the embedded category, of representable functors and their natural transformations, relates to the other objects in the larger functor category. It is an important tool that underlies several modern developments in algebraic geometry and representation theory. It is named after Nobuo Yoneda.

In category theory, a branch of mathematics, a natural transformation provides a way of transforming one functor into another while respecting the internal structure of the categories involved. Hence, a natural transformation can be considered to be a "morphism of functors". Informally, the notion of a natural transformation states that a particular map between functors can be done consistently over an entire category.

In mathematics, a monoidal category is a category $equipped with a bifunctor$

In mathematics, particularly homological algebra, an exact functor is a functor that preserves short exact sequences. Exact functors are convenient for algebraic calculations because they can be directly applied to presentations of objects. Much of the work in homological algebra is designed to cope with functors that fail to be exact, but in ways that can still be controlled.

In mathematics, especially in category theory, a closed monoidal category is a category that is both a monoidal category and a closed category in such a way that the structures are compatible.

This is a glossary of properties and concepts in category theory in mathematics.

In mathematics, specifically in category theory, hom-sets give rise to important functors to the category of sets. These functors are called hom-functors and have numerous applications in category theory and other branches of mathematics.

In category theory, an end of a functor $is a universal dinatural transformation from an object e of X to S .$

String diagrams are a formal graphical language for representing morphisms in monoidal categories, or more generally 2-cells in 2-categories. They are a prominent tool in applied category theory. When interpreted in the monoidal category of vector spaces and linear maps with the tensor product, string diagrams are called tensor networks or Penrose graphical notation. This has led to the development of categorical quantum mechanics where the axioms of quantum theory are expressed in the language of monoidal categories.

In category theory, monoidal functors are functors between monoidal categories which preserve the monoidal structure. More specifically, a monoidal functor between two monoidal categories consists of a functor between the categories, along with two coherence maps—a natural transformation and a morphism that preserve monoidal multiplication and unit, respectively. Mathematicians require these coherence maps to satisfy additional properties depending on how strictly they want to preserve the monoidal structure; each of these properties gives rise to a slightly different definition of monoidal functors

Suppose that $and are two monoidal categories and$

In category theory, a branch of mathematics, compact closed categories are a general context for treating dual objects. The idea of a dual object generalizes the more familiar concept of the dual of a finite-dimensional vector space. So, the motivating example of a compact closed category is FdVect, the category having finite-dimensional vector spaces as objects and linear maps as morphisms, with tensor product as the monoidal structure. Another example is Rel, the category having sets as objects and relations as morphisms, with Cartesian monoidal structure.

In category theory, a branch of mathematics, a dual object is an analogue of a dual vector space from linear algebra for objects in arbitrary monoidal categories. It is only a partial generalization, based upon the categorical properties of duality for finite-dimensional vector spaces. An object admitting a dual is called a dualizable object. In this formalism, infinite-dimensional vector spaces are not dualizable, since the dual vector space V^∗ doesn't satisfy the axioms. Often, an object is dualizable only when it satisfies some finiteness or compactness property.

In category theory, a branch of mathematics, dagger compact categories first appeared in 1989 in the work of Sergio Doplicher and John E. Roberts on the reconstruction of compact topological groups from their category of finite-dimensional continuous unitary representations. They also appeared in the work of John Baez and James Dolan as an instance of semistrict k-tuply monoidal n-categories, which describe general topological quantum field theories, for n = 1 and k = 3. They are a fundamental structure in Samson Abramsky and Bob Coecke's categorical quantum mechanics.

In the mathematical field of category theory, a dagger symmetric monoidal category is a monoidal category $that also possesses a dagger structure. That is, this category comes equipped not only with a tensor product in the category theoretic sense but also with a dagger structure, which is used to describe unitary morphisms and self-adjoint morphisms in : abstract analogues of those found in FdHilb, the category of finite-dimensional Hilbert spaces. This type of category was introduced by Peter Selinger as an intermediate structure between dagger categories and the dagger compact categories that are used in categorical quantum mechanics, an area that now also considers dagger symmetric monoidal categories when dealing with infinite-dimensional quantum mechanical concepts.$

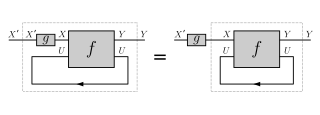
In category theory, a traced monoidal category is a category with some extra structure which gives a reasonable notion of feedback.

In mathematics, Hochschild homology (and cohomology) is a homology theory for associative algebras over rings. There is also a theory for Hochschild homology of certain functors. Hochschild cohomology was introduced by Gerhard Hochschild (1945) for algebras over a field, and extended to algebras over more general rings by Henri Cartan and Samuel Eilenberg (1956).

In category theory, a branch of mathematics, a rigid category is a monoidal category where every object is rigid, that is, has a dual X^* and a morphism 1 → X ⊗ X^* satisfying natural conditions. The category is called right rigid or left rigid according to whether it has right duals or left duals. They were first defined by Neantro Saavedra Rivano in his thesis on Tannakian categories.

In category theory, a branch of mathematics, Mac Lane's coherence theorem states, in the words of Saunders Mac Lane, “every diagram commutes”. But regarding a result about certain commutative diagrams, Kelly is states as follows: "no longer be seen as constituting the essence of a coherence theorem". More precisely, it states every formal diagram commutes, where "formal diagram" is an analog of well-formed formulae and terms in proof theory.

References

↑ Day, Brian (1970). "On closed categories of functors". Reports of the Midwest Category Seminar IV, Lecture Notes in Mathematics. 139: 1–38.
↑ Loregian, Fosco (2021). (Co)end Calculus. p. 51. arXiv: 1501.02503 . doi:10.1017/9781108778657. ISBN 9781108778657. S2CID 237839003.

External links

Day convolution at the nLab

This page is based on this Wikipedia article
Text is available under the CC BY-SA 4.0 license; additional terms may apply.
Images, videos and audio are available under their respective licenses.

[1] Day, Brian (1970). "On closed categories of functors". Reports of the Midwest Category Seminar IV, Lecture Notes in Mathematics. 139: 1–38.

[2] Loregian, Fosco (2021). (Co)end Calculus. p. 51. arXiv: 1501.02503 . doi:10.1017/9781108778657. ISBN 9781108778657. S2CID 237839003.

[1]

[2]