In topology, a field within mathematics, desuspension is an operation inverse to suspension. [1]
In general, given an n-dimensional space , the suspension has dimension n + 1. Thus, the operation of suspension creates a way of moving up in dimension. In the 1950s, to define a way of moving down, mathematicians introduced an inverse operation , called desuspension. [2] Therefore, given an n-dimensional space , the desuspension has dimension n – 1.
In general, .
The reasons to introduce desuspension:
In mathematics and computer science, currying is the technique of translating the evaluation of a function that takes multiple arguments into evaluating a sequence of functions, each with a single argument. For example, currying a function that takes three arguments creates a nested unary function , so that the code
In mathematics, a diffeomorphism is an isomorphism of smooth manifolds. It is an invertible function that maps one differentiable manifold to another such that both the function and its inverse are differentiable.
In algebra, a homomorphism is a structure-preserving map between two algebraic structures of the same type. The word homomorphism comes from the Ancient Greek language: ὁμός meaning "same" and μορφή meaning "form" or "shape". However, the word was apparently introduced to mathematics due to a (mis)translation of German ähnlich meaning "similar" to ὁμός meaning "same". The term "homomorphism" appeared as early as 1892, when it was attributed to the German mathematician Felix Klein (1849–1925).
In mathematics, a topological space is, roughly speaking, a geometrical space in which closeness is defined but cannot necessarily be measured by a numeric distance. More specifically, a topological space is a set whose elements are called points, along with an additional structure called a topology, which can be defined as a set of neighbourhoods for each point that satisfy some axioms formalizing the concept of closeness. There are several equivalent definitions of a topology, the most commonly used of which is the definition through open sets, which is easier than the others to manipulate.
In mathematics, an embedding is one instance of some mathematical structure contained within another instance, such as a group that is a subgroup.
In mathematics, homology is a general way of associating a sequence of algebraic objects, such as abelian groups or modules, with other mathematical objects such as topological spaces. Homology groups were originally defined in algebraic topology. Similar constructions are available in a wide variety of other contexts, such as abstract algebra, groups, Lie algebras, Galois theory, and algebraic geometry.
In gauge theory and mathematical physics, a topological quantum field theory is a quantum field theory which computes topological invariants.
In mathematics, the braid group on n strands, also known as the Artin braid group, is the group whose elements are equivalence classes of n-braids, and whose group operation is composition of braids. Example applications of braid groups include knot theory, where any knot may be represented as the closure of certain braids ; in mathematical physics where Artin's canonical presentation of the braid group corresponds to the Yang–Baxter equation ; and in monodromy invariants of algebraic geometry.
In topology, a branch of mathematics, the smash product of two pointed spaces (i.e. topological spaces with distinguished basepoints) (X,x0) and (Y, y0) is the quotient of the product space X × Y under the identifications (x, y0) ∼ (x0, y) for all x in X and y in Y. The smash product is itself a pointed space, with basepoint being the equivalence class of (x0, y0). The smash product is usually denoted X ∧ Y or X ⨳ Y. The smash product depends on the choice of basepoints (unless both X and Y are homogeneous).
In mathematics, in the subfield of geometric topology, the mapping class group is an important algebraic invariant of a topological space. Briefly, the mapping class group is a certain discrete group corresponding to symmetries of the space.
In algebraic topology, a branch of mathematics, a spectrum is an object representing a generalized cohomology theory. Every such cohomology theory is representable, as follows from Brown's representability theorem. This means that, given a cohomology theory
,
In mathematics, a pointed space or based space is a topological space with a distinguished point, the basepoint. The distinguished point is just simply one particular point, picked out from the space, and given a name, such as that remains unchanged during subsequent discussion, and is kept track of during all operations.
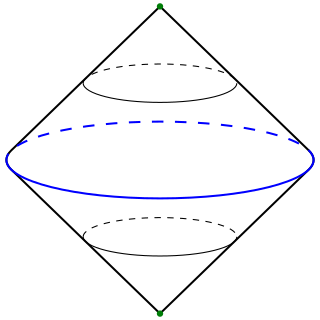
In topology, a branch of mathematics, the suspension of a topological space X is intuitively obtained by stretching X into a cylinder and then collapsing both end faces to points. One views X as "suspended" between these end points. The suspension of X is denoted by SX or susp(X).
In mathematics, the homotopy category is a category built from the category of topological spaces which in a sense identifies two spaces that have the same shape. The phrase is in fact used for two different categories, as discussed below.
In topology, a branch of mathematics, the loop space ΩX of a pointed topological space X is the space of (based) loops in X, i.e. continuous pointed maps from the pointed circle S1 to X, equipped with the compact-open topology. Two loops can be multiplied by concatenation. With this operation, the loop space is an A∞-space. That is, the multiplication is homotopy-coherently associative.
In mathematics, nuclear spaces are topological vector spaces that can be viewed as a generalization of finite dimensional Euclidean spaces and share many of their desirable properties. Nuclear spaces are however quite different from Hilbert spaces, another generalization of finite dimensional Euclidean spaces. They were introduced by Alexander Grothendieck.
In mathematics, stable homotopy theory is the part of homotopy theory concerned with all structure and phenomena that remain after sufficiently many applications of the suspension functor. A founding result was the Freudenthal suspension theorem, which states that given any pointed space , the homotopy groups stabilize for sufficiently large. In particular, the homotopy groups of spheres stabilize for . For example,
String diagrams are a formal graphical language for representing morphisms in monoidal categories, or more generally 2-cells in 2-categories. They are a prominent tool in applied category theory. When interpreted in the monoidal category of vector spaces and linear maps with the tensor product, string diagrams are called tensor networks or Penrose graphical notation. This has led to the development of categorical quantum mechanics where the axioms of quantum theory are expressed in the language of monoidal categories.
In mathematics, a space is a set with some added structure. While modern mathematics uses many types of spaces, such as Euclidean spaces, linear spaces, topological spaces, Hilbert spaces, or probability spaces, it does not define the notion of "space" itself.
This is a glossary of properties and concepts in algebraic topology in mathematics.
