Development (differential geometry)

Last updated March 24, 2019

In classical differential geometry, development refers to the simple idea of rolling one smooth surface over another in Euclidean space. For example, the tangent plane to a surface (such as the sphere or the cylinder) at a point can be rolled around the surface to obtain the tangent plane at other points.

Differential geometry is a mathematical discipline that uses the techniques of differential calculus, integral calculus, linear algebra and multilinear algebra to study problems in geometry. The theory of plane and space curves and surfaces in the three-dimensional Euclidean space formed the basis for development of differential geometry during the 18th century and the 19th century.

In geometry, Euclidean space encompasses the two-dimensional Euclidean plane, the three-dimensional space of Euclidean geometry, and similar spaces of higher dimension. It is named after the Ancient Greek mathematician Euclid of Alexandria. The term "Euclidean" distinguishes these spaces from other types of spaces considered in modern geometry. Euclidean spaces also generalize to higher dimensions.

A sphere is a perfectly round geometrical object in three-dimensional space that is the surface of a completely round ball.

Properties

The tangential contact between the surfaces being rolled over one another provides a relation between points on the two surfaces. If this relation is (perhaps only in a local sense) a bijection between the surfaces, then the two surfaces are said to be developable on each other or developments of each other. Differently put, the correspondence provides an isometry, locally, between the two surfaces.

In mathematics, a phenomenon is sometimes said to occur locally if, roughly speaking, it occurs on sufficiently small or arbitrarily small neighborhoods of points.

Bijection one to one and onto mapping of a set X to a set Y

In mathematics, a bijection, bijective function, or one-to-one correspondence is a function between the elements of two sets, where each element of one set is paired with exactly one element of the other set, and each element of the other set is paired with exactly one element of the first set. There are no unpaired elements. In mathematical terms, a bijective function f: X → Y is a one-to-one (injective) and onto (surjective) mapping of a set X to a set Y.

In mathematics, an isometry is a distance-preserving transformation between metric spaces, usually assumed to be bijective.

In particular, if one of the surfaces is a plane, then the other is called a developable surface: thus a developable surface is one which is locally isometric to a plane. The cylinder is developable, but the sphere is not.

In mathematics, a developable surface is a smooth surface with zero Gaussian curvature. That is, it is a surface that can be flattened onto a plane without distortion. Conversely, it is a surface which can be made by transforming a plane. In three dimensions all developable surfaces are ruled surfaces. There are developable surfaces in R⁴ which are not ruled.

Flat connections

Development can be generalized further using flat connections. From this point of view, rolling the tangent plane over a surface defines an affine connection on the surface (it provides an example of parallel transport along a curve), and a developable surface is one for which this connection is flat.

In the branch of mathematics called differential geometry, an affine connection is a geometric object on a smooth manifold which connects nearby tangent spaces, so it permits tangent vector fields to be differentiated as if they were functions on the manifold with values in a fixed vector space. The notion of an affine connection has its roots in 19th-century geometry and tensor calculus, but was not fully developed until the early 1920s, by Élie Cartan and Hermann Weyl. The terminology is due to Cartan and has its origins in the identification of tangent spaces in Euclidean space $R n$ by translation: the idea is that a choice of affine connection makes a manifold look infinitesimally like Euclidean space not just smoothly, but as an affine space.

In geometry, parallel transport is a way of transporting geometrical data along smooth curves in a manifold. If the manifold is equipped with an affine connection, then this connection allows one to transport vectors of the manifold along curves so that they stay parallel with respect to the connection.

Curve object similar to a line but which is not required to be straight

In mathematics, a curve is, generally speaking, an object similar to a line but that need not be straight. Thus, a curve is a generalization of a line, in that its curvature need not be zero.

More generally any flat Cartan connection on a manifold defines a development of that manifold onto the model space. Perhaps the most famous example is the development of conformally flat n-manifolds, in which the model-space is the n-sphere. The development of a conformally flat manifold is a conformal local diffeomorphism from the universal cover of the manifold to the n-sphere.

In the mathematical field of differential geometry, a Cartan connection is a flexible generalization of the notion of an affine connection. It may also be regarded as a specialization of the general concept of a principal connection, in which the geometry of the principal bundle is tied to the geometry of the base manifold using a solder form. Cartan connections describe the geometry of manifolds modelled on homogeneous spaces.

Manifold topological space that at each point resembles Euclidean space

In mathematics, a manifold is a topological space that locally resembles Euclidean space near each point. More precisely, each point of an n-dimensional manifold has a neighbourhood that is homeomorphic to the Euclidean space of dimension n. In this more precise terminology, a manifold is referred to as an n-manifold.

In mathematics, a Klein geometry is a type of geometry motivated by Felix Klein in his influential Erlangen program. More specifically, it is a homogeneous space X together with a transitive action on X by a Lie group G, which acts as the symmetry group of the geometry.

Undevelopable surfaces

The class of double-curved surfaces (undevelopable surfaces) contains objects that cannot be simply unfolded (developed). Such surfaces can be developed only approximately with some distortions of linear surface elements (see the Stretched grid method)

The stretched grid method (SGM) is a numerical technique for finding approximate solutions of various mathematical and engineering problems that can be related to an elastic grid behavior. In particular, meteorologists use the stretched grid method for weather prediction and engineers use the stretched grid method to design tents and other tensile structures.

Related Research Articles

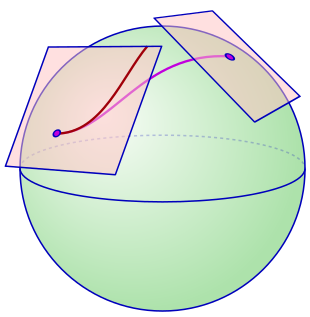
In mathematics, curvature is any of a number of loosely related concepts in different areas of geometry. Intuitively, curvature is the amount by which a geometric object such as a surface deviates from being a flat plane, or a curve from being straight as in the case of a line, but this is defined in different ways depending on the context. There is a key distinction between extrinsic curvature, which is defined for objects embedded in another space – in a way that relates to the radius of curvature of circles that touch the object – and intrinsic curvature, which is defined in terms of the lengths of curves within a Riemannian manifold.

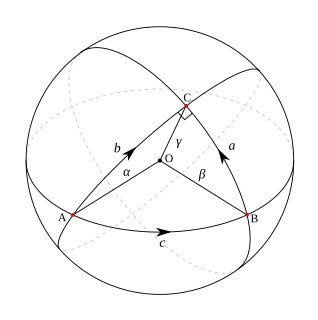
In differential geometry, a geodesic is a generalization of the notion of a "straight line" to "curved spaces". The term "geodesic" comes from geodesy, the science of measuring the size and shape of Earth; in the original sense, a geodesic was the shortest route between two points on the Earth's surface, namely, a segment of a great circle. The term has been generalized to include measurements in much more general mathematical spaces; for example, in graph theory, one might consider a geodesic between two vertices/nodes of a graph.

In mathematics, particularly in complex analysis, a Riemann surface is a one-dimensional complex manifold. These surfaces were first studied by and are named after Bernhard Riemann. Riemann surfaces can be thought of as deformed versions of the complex plane: locally near every point they look like patches of the complex plane, but the global topology can be quite different. For example, they can look like a sphere or a torus or several sheets glued together.

Riemannian geometry is the branch of differential geometry that studies Riemannian manifolds, smooth manifolds with a Riemannian metric, i.e. with an inner product on the tangent space at each point that varies smoothly from point to point. This gives, in particular, local notions of angle, length of curves, surface area and volume. From those, some other global quantities can be derived by integrating local contributions.

In differential geometry, the tangent bundle of a differentiable manifold $is a manifold which assembles all the tangent vectors in M . As a set, it is given by the disjoint union of the tangent spaces of M . That is,$

In differential geometry, the Gaussian curvature or Gauss curvatureΚ of a surface at a point is the product of the principal curvatures, κ₁ and κ₂, at the given point:

In mathematics, conformal geometry is the study of the set of angle-preserving (conformal) transformations on a space.

In mathematics, a moving frame is a flexible generalization of the notion of an ordered basis of a vector space often used to study the extrinsic differential geometry of smooth manifolds embedded in a homogeneous space.

This is a glossary of some terms used in Riemannian geometry and metric geometry — it doesn't cover the terminology of differential topology.

In mathematics, a differentiable manifold is a type of manifold that is locally similar enough to a linear space to allow one to do calculus. Any manifold can be described by a collection of charts, also known as an atlas. One may then apply ideas from calculus while working within the individual charts, since each chart lies within a linear space to which the usual rules of calculus apply. If the charts are suitably compatible, then computations done in one chart are valid in any other differentiable chart.

In mathematics, the differential geometry of surfaces deals with the differential geometry of smooth surfaces with various additional structures, most often, a Riemannian metric. Surfaces have been extensively studied from various perspectives: extrinsically, relating to their embedding in Euclidean space and intrinsically, reflecting their properties determined solely by the distance within the surface as measured along curves on the surface. One of the fundamental concepts investigated is the Gaussian curvature, first studied in depth by Carl Friedrich Gauss, who showed that curvature was an intrinsic property of a surface, independent of its isometric embedding in Euclidean space.

In mathematics, the Riemannian connection on a surface or Riemannian 2-manifold refers to several intrinsic geometric structures discovered by Tullio Levi-Civita, Élie Cartan and Hermann Weyl in the early part of the twentieth century: parallel transport, covariant derivative and connection form. These concepts were put in their current form with principal bundles only in the 1950s. The classical nineteenth century approach to the differential geometry of surfaces, due in large part to Carl Friedrich Gauss, has been reworked in this modern framework, which provides the natural setting for the classical theory of the moving frame as well as the Riemannian geometry of higher-dimensional Riemannian manifolds. This account is intended as an introduction to the theory of connections.

In differential geometry and the study of Lie groups, a parabolic geometry is a homogeneous space G/P which is the quotient of a semisimple Lie group G by a parabolic subgroup P. More generally, the curved analogs of a parabolic geometry in this sense is also called a parabolic geometry: any geometry that is modeled on such a space by means of a Cartan connection.

References

Sharpe, R.W. (1997). Differential Geometry: Cartan's Generalization of Klein's Erlangen Program. Springer-Verlag, New York. ISBN 0-387-94732-9.

This page is based on this Wikipedia article
Text is available under the CC BY-SA 4.0 license; additional terms may apply.
Images, videos and audio are available under their respective licenses.