
In mathematics, more specifically calculus, L'Hôpital's rule or L'Hospital's rule, also known as Bernoulli's rule, is a theorem which provides a technique to evaluate limits of indeterminate forms. Application of the rule often converts an indeterminate form to an expression that can be easily evaluated by substitution. The rule is named after the 17th-century French mathematician Guillaume de l'Hôpital. Although the rule is often attributed to L'Hôpital, the theorem was first introduced to him in 1694 by the Swiss mathematician Johann Bernoulli.
In mathematics, the infimum of a subset of a partially ordered set is a greatest element in that is less than or equal to each element of if such an element exists. Consequently, the term greatest lower bound is also commonly used.

In mathematics, the limit inferior and limit superior of a sequence can be thought of as limiting bounds on the sequence. They can be thought of in a similar fashion for a function. For a set, they are the infimum and supremum of the set's limit points, respectively. In general, when there are multiple objects around which a sequence, function, or set accumulates, the inferior and superior limits extract the smallest and largest of them; the type of object and the measure of size is context-dependent, but the notion of extreme limits is invariant. Limit inferior is also called infimum limit, limit infimum, liminf, inferior limit, lower limit, or inner limit; limit superior is also known as supremum limit, limit supremum, limsup, superior limit, upper limit, or outer limit.
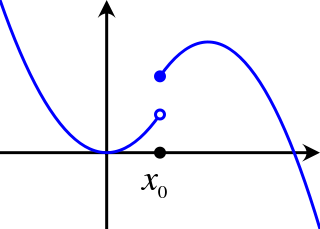
In mathematical analysis, semicontinuity is a property of extended real-valued functions that is weaker than continuity. An extended real-valued function is uppersemicontinuous at a point if, roughly speaking, the function values for arguments near are not much higher than
In the mathematical field of real analysis, the monotone convergence theorem is any of a number of related theorems proving the convergence of monotonic sequences that are also bounded. Informally, the theorems state that if a sequence is increasing and bounded above by a supremum, then the sequence will converge to the supremum; in the same way, if a sequence is decreasing and is bounded below by an infimum, it will converge to the infimum.

In calculus, the extreme value theorem states that if a real-valued function is continuous on the closed interval , then must attain a maximum and a minimum, each at least once. That is, there exist numbers and in such that:
In mathematics, Fatou's lemma establishes an inequality relating the Lebesgue integral of the limit inferior of a sequence of functions to the limit inferior of integrals of these functions. The lemma is named after Pierre Fatou.
In mathematics, the limit of a sequence of sets is a set whose elements are determined by the sequence in either of two equivalent ways: (1) by upper and lower bounds on the sequence that converge monotonically to the same set and (2) by convergence of a sequence of indicator functions which are themselves real-valued. As is the case with sequences of other objects, convergence is not necessary or even usual.
In mathematics, smooth functions and analytic functions are two very important types of functions. One can easily prove that any analytic function of a real argument is smooth. The converse is not true, as demonstrated with the counterexample below.

In mathematics, the oscillation of a function or a sequence is a number that quantifies how much that sequence or function varies between its extreme values as it approaches infinity or a point. As is the case with limits, there are several definitions that put the intuitive concept into a form suitable for a mathematical treatment: oscillation of a sequence of real numbers, oscillation of a real-valued function at a point, and oscillation of a function on an interval.
In mathematics, the exponential function can be characterized in many ways. The following characterizations (definitions) are most common. This article discusses why each characterization makes sense, and why the characterizations are independent of and equivalent to each other. As a special case of these considerations, it will be demonstrated that the three most common definitions given for the mathematical constant e are equivalent to each other.
In number theory, natural density is one method to measure how "large" a subset of the set of natural numbers is. It relies chiefly on the probability of encountering members of the desired subset when combing through the interval [1, n] as n grows large.
In the field of mathematical analysis for the calculus of variations, Γ-convergence (Gamma-convergence) is a notion of convergence for functionals. It was introduced by Ennio de Giorgi.
In calculus, a branch of mathematics, the notions of one-sided differentiability and semi-differentiability of a real-valued function f of a real variable are weaker than differentiability. Specifically, the function f is said to be right differentiable at a point a if, roughly speaking, a derivative can be defined as the function's argument x moves to a from the right, and left differentiable at a if the derivative can be defined as x moves to a from the left.
In mathematics, the Fatou–Lebesgue theorem establishes a chain of inequalities relating the integrals of the limit inferior and the limit superior of a sequence of functions to the limit inferior and the limit superior of integrals of these functions. The theorem is named after Pierre Fatou and Henri Léon Lebesgue.
In mathematics, the concepts of essential infimum and essential supremum are related to the notions of infimum and supremum, but adapted to measure theory and functional analysis, where one often deals with statements that are not valid for all elements in a set, but rather almost everywhere, i.e., except on a set of measure zero.
In mathematics, the Hardy–Littlewood maximal operatorM is a significant non-linear operator used in real analysis and harmonic analysis. It takes a locally integrable function f : Rd → C and returns another function Mf that, at each point x ∈ Rd, gives the maximum average value that f can have on balls centered at that point. More precisely,
In mathematics, the limit comparison test (LCT) is a method of testing for the convergence of an infinite series.
In mathematics, specifically in number theory, the extremal orders of an arithmetic function are best possible bounds of the given arithmetic function. Specifically, if f(n) is an arithmetic function and m(n) is a non-decreasing function that is ultimately positive and
In mathematics, a càdlàg, RCLL, or corlol function is a function defined on the real numbers that is everywhere right-continuous and has left limits everywhere. Càdlàg functions are important in the study of stochastic processes that admit jumps, unlike Brownian motion, which has continuous sample paths. The collection of càdlàg functions on a given domain is known as Skorokhod space.













