Distance decay

Last updated October 12, 2024

Distance decay is a geographical term which describes the effect of distance on cultural or spatial interactions.^[1] The distance decay effect states that the interaction between two locales declines as the distance between them increases. Once the distance is outside of the two locales' activity space, their interactions begin to decrease. It is thus an assertion that the mathematics of the inverse square law in physics can be applied to many geographic phenomena, and is one of the ways in which physics principles such as gravity are often applied metaphorically to geographic situations.

Mathematical models

Distance decay is graphically represented by a curving line that swoops concavely downward as distance along the x-axis increases. Distance decay can be mathematically represented as an inverse-square law by the expression

I={\text{constant}}\times d^{-2}

or

I\propto 1/d^{2},

where $I$ is interaction and $d$ is distance. In practice, it is often parameterized to fit a specific situation, such as

I={\frac {A}{(d+B)^{k}}},

in which the constant $A$ is a vertical stretching factor, $B$ is a horizontal shift (so that the curve has a y-axis intercept at a finite value), and $k$ is the decay power.

It can take other forms such as negative exponential,^[2] i.e.

I\propto e^{-d}.

In addition to fitting the parameters, a cutoff value can be added to a distance decay function to specify a distance beyond which spatial interaction drops to zero, or to delineate a "zone of indifference" in which all interactions have the same strength.^[3]

Applications

Distance decay is evident in town/city centres. It can refer to various things which decline with greater distance from the center of the central business district (CBD):

density of pedestrian traffic
street quality
quality of shops (depending on definitions of 'quality' and 'center')
height of buildings
price of land

Distance decay weighs into the decision to migrate, leading many migrants to move less far.

With the advent of faster travel and communications technology, such as telegraphs, telephones, broadcasting, and internet, the effects of distance have been reduced, a trend known as time-space convergence.^[4] Exceptions include places previously connected by now-abandoned railways, for example, have fallen off the beaten path.

Related concepts

Related terms include "friction of distance", which describes the forces that create the distance decay effect. Waldo R. Tobler's "First law of geography", an informal statement that "All things are related, but near things are more related than far things," and the mathematical principle spatial autocorrelation are similar expressions of distance decay effects. "Loss of Strength Gradient" holds that the amount of a nation's military power that could be brought to bear in any part of the world depends on geographic distance.

Related Research Articles

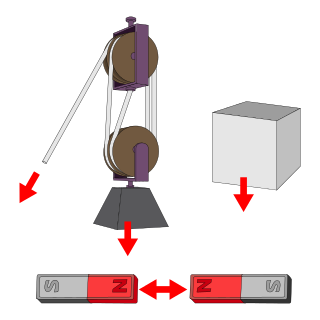
A force is an influence that can cause an object to change its velocity unless counterbalanced by other forces. The concept of force makes the everyday notion of pushing or pulling mathematically precise. Because the magnitude and direction of a force are both important, force is a vector quantity. The SI unit of force is the newton (N), and force is often represented by the symbol $F$ .

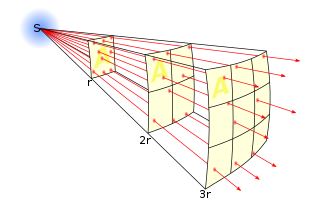
In science, an inverse-square law is any scientific law stating that the observed "intensity" of a specified physical quantity is inversely proportional to the square of the distance from the source of that physical quantity. The fundamental cause for this can be understood as geometric dilution corresponding to point-source radiation into three-dimensional space.

In mathematics, two sequences of numbers, often experimental data, are proportional or directly proportional if their corresponding elements have a constant ratio. The ratio is called coefficient of proportionality and its reciprocal is known as constant of normalization. Two sequences are inversely proportional if corresponding elements have a constant product, also called the coefficient of proportionality.

In physics, a fifth force refers to a hypothetical fundamental interaction beyond the four known interactions in nature: gravitational, electromagnetic, strong nuclear, and weak nuclear forces. Some speculative theories have proposed a fifth force to explain various anomalous observations that do not fit existing theories. The specific characteristics of a putative fifth force depend on which hypothesis is being advanced. No evidence to support these models has been found.

Newton's law of universal gravitation states that every particle attracts every other particle in the universe with a force that is proportional to the product of their masses and inversely proportional to the square of the distance between their centers. Separated objects attract and are attracted as if all their mass were concentrated at their centers. The publication of the law has become known as the "first great unification", as it marked the unification of the previously described phenomena of gravity on Earth with known astronomical behaviors.

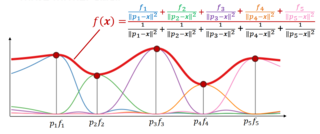
Inverse distance weighting (IDW) is a type of deterministic method for multivariate interpolation with a known scattered set of points. The assigned values to unknown points are calculated with a weighted average of the values available at the known points. This method can also be used to create spatial weights matrices in spatial autocorrelation analyses.

The surface gravity, g, of an astronomical object is the gravitational acceleration experienced at its surface at the equator, including the effects of rotation. The surface gravity may be thought of as the acceleration due to gravity experienced by a hypothetical test particle which is very close to the object's surface and which, in order not to disturb the system, has negligible mass. For objects where the surface is deep in the atmosphere and the radius not known, the surface gravity is given at the 1 bar pressure level in the atmosphere.

Spatial ecology studies the ultimate distributional or spatial unit occupied by a species. In a particular habitat shared by several species, each of the species is usually confined to its own microhabitat or spatial niche because two species in the same general territory cannot usually occupy the same ecological niche for any significant length of time.

The First Law of Geography, according to Waldo Tobler, is "everything is related to everything else, but near things are more related than distant things." This first law is the foundation of the fundamental concepts of spatial dependence and spatial autocorrelation and is utilized specifically for the inverse distance weighting method for spatial interpolation and to support the regionalized variable theory for kriging. The first law of geography is the fundamental assumption used in all spatial analysis.

<span class="mw-page-title-main">Spatial analysis</span> Formal techniques which study entities using their topological, geometric, or geographic properties

Spatial analysis is any of the formal techniques which studies entities using their topological, geometric, or geographic properties. Spatial analysis includes a variety of techniques using different analytic approaches, especially spatial statistics. It may be applied in fields as diverse as astronomy, with its studies of the placement of galaxies in the cosmos, or to chip fabrication engineering, with its use of "place and route" algorithms to build complex wiring structures. In a more restricted sense, spatial analysis is geospatial analysis, the technique applied to structures at the human scale, most notably in the analysis of geographic data. It may also be applied to genomics, as in transcriptomics data.

In quantum field theory and statistical mechanics, the Hohenberg–Mermin–Wagner theorem or Mermin–Wagner theorem states that continuous symmetries cannot be spontaneously broken at finite temperature in systems with sufficiently short-range interactions in dimensions $d \leq 2$ . Intuitively, this theorem implies that long-range fluctuations can be created with little energy cost, and since they increase the entropy, they are favored.

Friction of distance is a core principle of geography that states that movement incurs some form of cost, in the form of physical effort, energy, time, and/or the expenditure of other resources, and that these costs are proportional to the distance traveled. This cost is thus a resistance against movement, analogous to the effect of friction against movement in classical mechanics. The subsequent preference for minimizing distance and its cost underlies a vast array of geographic patterns from economic agglomeration to wildlife migration, as well as many of the theories and techniques of spatial analysis, such as Tobler's first law of geography, network routing, and cost distance analysis. To a large degree, friction of distance is the primary reason why geography is relevant to many aspects of the world, although its importance has been decreasing with the development of transportation and communication technologies.

The expansion of the universe is the increase in distance between gravitationally unbound parts of the observable universe with time. It is an intrinsic expansion, so it does not mean that the universe expands "into" anything or that space exists "outside" it. To any observer in the universe, it appears that all but the nearest galaxies recede at speeds that are proportional to their distance from the observer, on average. While objects cannot move faster than light, this limitation applies only with respect to local reference frames and does not limit the recession rates of cosmologically distant objects.

In classical mechanics, Newton's theorem of revolving orbits identifies the type of central force needed to multiply the angular speed of a particle by a factor k without affecting its radial motion. Newton applied his theorem to understanding the overall rotation of orbits that is observed for the Moon and planets. The term "radial motion" signifies the motion towards or away from the center of force, whereas the angular motion is perpendicular to the radial motion.

In statistics, Moran's I is a measure of spatial autocorrelation developed by Patrick Alfred Pierce Moran. Spatial autocorrelation is characterized by a correlation in a signal among nearby locations in space. Spatial autocorrelation is more complex than one-dimensional autocorrelation because spatial correlation is multi-dimensional and multi-directional.

Proximity analysis is a class of spatial analysis tools and algorithms that employ geographic distance as a central principle. Distance is fundamental to geographic inquiry and spatial analysis, due to principles such as the friction of distance, Tobler's first law of geography, and Spatial autocorrelation, which are incorporated into analytical tools. Proximity methods are thus used in a variety of applications, especially those that involve movement and interaction.

A boundary problem in analysis is a phenomenon in which geographical patterns are differentiated by the shape and arrangement of boundaries that are drawn for administrative or measurement purposes. The boundary problem occurs because of the loss of neighbors in analyses that depend on the values of the neighbors. While geographic phenomena are measured and analyzed within a specific unit, identical spatial data can appear either dispersed or clustered depending on the boundary placed around the data. In analysis with point data, dispersion is evaluated as dependent of the boundary. In analysis with areal data, statistics should be interpreted based upon the boundary.

This glossary of physics is a list of definitions of terms and concepts relevant to physics, its sub-disciplines, and related fields, including mechanics, materials science, nuclear physics, particle physics, and thermodynamics. For more inclusive glossaries concerning related fields of science and technology, see Glossary of chemistry terms, Glossary of astronomy, Glossary of areas of mathematics, and Glossary of engineering.

The Gurzhi effect was theoretically predicted by Radii Gurzhi in 1963, and it consists of decreasing of electric resistance $of a finite size conductor with increasing of its temperature . Gurzhi effect usually being considered as the evidence of electron hydrodynamic transport in conducting media. The mechanism of Gurzhi effect is the following. The value of the resistance of the conductor is inverse to the — a mean free path corresponding to the momentum loss from the electrons+phonons system where is the average distance which electron pass between two consecutive interactions with a boundary, and is a mean free path corresponding to other possibilities of momentum loss. The electron reflection from the boundary is assumed to be diffusive.$

Arbia's law of geography states, "Everything is related to everything else, but things observed at a coarse spatial resolution are more related than things observed at a finer resolution." Originally proposed as the 2nd law of geography, this is one of several laws competing for that title. Because of this, Arbia's law is sometimes referred to as the second law of geography, or Arbia's second law of geography.

References

Taverna, Kristin; Xi, Weimin. "Working Group on Distance Decay". University of North Carolina at Chapel Hill. Archived from the original on 2011-09-30. Retrieved 2006-08-31.
De Blij, Harm J.; Murphy, Alexander B.; Fouberg, Erin Hogan (2007). Human geography: people, place, and culture (8th ed.). New York: J. Wiley. pp. 68–69. ISBN 978-0-471-67951-6. OCLC 62132765.

↑ Taylor, Peter J. (1983). Distance Decay in Spatial Interactions (PDF). ISBN 0-86094-090-X. OCLC 12306293.
↑ Nekola, Jeffrey C.; White, Peter S. (July 1999). "The distance decay of similarity in biogeography and ecology" (PDF). Journal of Biogeography . 26 (4): 867–878. Bibcode:1999JBiog..26..867N. doi:10.1046/j.1365-2699.1999.00305.x. ISSN 0305-0270.
↑ Grekousis, George (2020). Spatial analysis methods and practice (First ed.). New York, NY: Cambridge University Press. pp. 20–23. ISBN 978-1-108-61452-8.
↑ Matous, Petr; Todo, Yasuyuki; Mojo, Dagne (July 2013). "Boots are made for walking: interactions across physical and social space in infrastructure-poor regions". Journal of Transport Geography . 31: 226–235. Bibcode:2013JTGeo..31..226M. doi:10.1016/j.jtrangeo.2013.04.001.

This page is based on this Wikipedia article
Text is available under the CC BY-SA 4.0 license; additional terms may apply.
Images, videos and audio are available under their respective licenses.

[1] Taylor, Peter J. (1983). Distance Decay in Spatial Interactions (PDF). ISBN 0-86094-090-X. OCLC 12306293.

[2] Nekola, Jeffrey C.; White, Peter S. (July 1999). "The distance decay of similarity in biogeography and ecology" (PDF). Journal of Biogeography . 26 (4): 867–878. Bibcode:1999JBiog..26..867N. doi:10.1046/j.1365-2699.1999.00305.x. ISSN 0305-0270.

[3] Grekousis, George (2020). Spatial analysis methods and practice (First ed.). New York, NY: Cambridge University Press. pp. 20–23. ISBN 978-1-108-61452-8.

[4] Matous, Petr; Todo, Yasuyuki; Mojo, Dagne (July 2013). "Boots are made for walking: interactions across physical and social space in infrastructure-poor regions". Journal of Transport Geography . 31: 226–235. Bibcode:2013JTGeo..31..226M. doi:10.1016/j.jtrangeo.2013.04.001.

[1]

[2]

[3]

[4]