An electronic oscillator is an electronic circuit that produces a periodic, oscillating or alternating current (AC) signal, usually a sine wave, square wave or a triangle wave, powered by a direct current (DC) source. Oscillators are found in many electronic devices, such as radio receivers, television sets, radio and television broadcast transmitters, computers, computer peripherals, cellphones, radar, and many other devices.
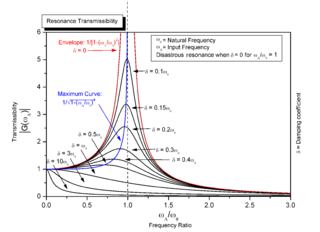
Resonance is the phenomenon, pertaining to oscillatory dynamical systems, wherein amplitude rises are caused by an external force with time-varying amplitude with the same frequency of variation as the natural frequency of the system. The amplitude rises that occur are a result of the fact that applied external forces at the natural frequency entail a net increase in mechanical energy of the system.

In physics, a plasmon is a quantum of plasma oscillation. Just as light consists of photons, the plasma oscillation consists of plasmons. The plasmon can be considered as a quasiparticle since it arises from the quantization of plasma oscillations, just like phonons are quantizations of mechanical vibrations. Thus, plasmons are collective oscillations of the free electron gas density. For example, at optical frequencies, plasmons can couple with a photon to create another quasiparticle called a plasmon polariton.
In classical and quantum mechanics, geometric phase is a phase difference acquired over the course of a cycle, when a system is subjected to cyclic adiabatic processes, which results from the geometrical properties of the parameter space of the Hamiltonian. The phenomenon was independently discovered by S. Pancharatnam (1956), in classical optics and by H. C. Longuet-Higgins (1958) in molecular physics; it was generalized by Michael Berry in (1984). It is also known as the Pancharatnam–Berry phase, Pancharatnam phase, or Berry phase. It can be seen in the conical intersection of potential energy surfaces and in the Aharonov–Bohm effect. Geometric phase around the conical intersection involving the ground electronic state of the C6H3F3+ molecular ion is discussed on pages 385–386 of the textbook by Bunker and Jensen. In the case of the Aharonov–Bohm effect, the adiabatic parameter is the magnetic field enclosed by two interference paths, and it is cyclic in the sense that these two paths form a loop. In the case of the conical intersection, the adiabatic parameters are the molecular coordinates. Apart from quantum mechanics, it arises in a variety of other wave systems, such as classical optics. As a rule of thumb, it can occur whenever there are at least two parameters characterizing a wave in the vicinity of some sort of singularity or hole in the topology; two parameters are required because either the set of nonsingular states will not be simply connected, or there will be nonzero holonomy.
In electromagnetism, Brillouin scattering, named after Léon Brillouin, refers to the interaction of light with the material waves in a medium. It is mediated by the refractive index dependence on the material properties of the medium; as described in optics, the index of refraction of a transparent material changes under deformation.
In physics, Landau damping, named after its discoverer, Soviet physicist Lev Davidovich Landau (1908–68), is the effect of damping of longitudinal space charge waves in plasma or a similar environment. This phenomenon prevents an instability from developing, and creates a region of stability in the parameter space. It was later argued by Donald Lynden-Bell that a similar phenomenon was occurring in galactic dynamics, where the gas of electrons interacting by electrostatic forces is replaced by a "gas of stars" interacting by gravitational forces. Landau damping can be manipulated exactly in numerical simulations such as particle-in-cell simulation. It was proved to exist experimentally by Malmberg and Wharton in 1964, almost two decades after its prediction by Landau in 1946.

Electromagnetically induced transparency (EIT) is a coherent optical nonlinearity which renders a medium transparent within a narrow spectral range around an absorption line. Extreme dispersion is also created within this transparency "window" which leads to "slow light", described below. It is in essence a quantum interference effect that permits the propagation of light through an otherwise opaque atomic medium.

Neutrino oscillation is a quantum mechanical phenomenon in which a neutrino created with a specific lepton family number can later be measured to have a different lepton family number. The probability of measuring a particular flavor for a neutrino varies between three known states, as it propagates through space.
In physics, an oscillon is a soliton-like phenomenon that occurs in granular and other dissipative media. Oscillons in granular media result from vertically vibrating a plate with a layer of uniform particles placed freely on top. When the sinusoidal vibrations are of the correct amplitude and frequency and the layer of sufficient thickness, a localized wave, referred to as an oscillon, can be formed by locally disturbing the particles. This meta-stable state will remain for a long time in the absence of further perturbation. An oscillon changes form with each collision of the grain layer and the plate, switching between a peak that projects above the grain layer to a crater like depression with a small rim. This self-sustaining state was named by analogy with the soliton, which is a localized wave that maintains its integrity as it moves. Whereas solitons occur as travelling waves in a fluid or as electromagnetic waves in a waveguide, oscillons may be stationary.

In the study of dynamical systems, the van der Pol oscillator is a non-conservative, oscillating system with non-linear damping. It evolves in time according to the second-order differential equation

An optical parametric oscillator (OPO) is a parametric oscillator that oscillates at optical frequencies. It converts an input laser wave with frequency into two output waves of lower frequency by means of second-order nonlinear optical interaction. The sum of the output waves' frequencies is equal to the input wave frequency: . For historical reasons, the two output waves are called "signal" and "idler", where the output wave with higher frequency is the "signal". A special case is the degenerate OPO, when the output frequency is one-half the pump frequency, , which can result in half-harmonic generation when signal and idler have the same polarization.

In classical mechanics, anharmonicity is the deviation of a system from being a harmonic oscillator. An oscillator that is not oscillating in harmonic motion is known as an anharmonic oscillator where the system can be approximated to a harmonic oscillator and the anharmonicity can be calculated using perturbation theory. If the anharmonicity is large, then other numerical techniques have to be used. In reality all oscillating systems are anharmonic, but most approximate the harmonic oscillator the smaller the amplitude of the oscillation is.

A parametric oscillator is a driven harmonic oscillator in which the oscillations are driven by varying some parameters of the system at some frequencies, typically different from the natural frequency of the oscillator. A simple example of a parametric oscillator is a child pumping a playground swing by periodically standing and squatting to increase the size of the swing's oscillations. The child's motions vary the moment of inertia of the swing as a pendulum. The "pump" motions of the child must be at twice the frequency of the swing's oscillations. Examples of parameters that may be varied are the oscillator's resonance frequency and damping .

In physics, a quantum vortex represents a quantized flux circulation of some physical quantity. In most cases, quantum vortices are a type of topological defect exhibited in superfluids and superconductors. The existence of quantum vortices was first predicted by Lars Onsager in 1949 in connection with superfluid helium. Onsager reasoned that quantisation of vorticity is a direct consequence of the existence of a superfluid order parameter as a spatially continuous wavefunction. Onsager also pointed out that quantum vortices describe the circulation of superfluid and conjectured that their excitations are responsible for superfluid phase transitions. These ideas of Onsager were further developed by Richard Feynman in 1955 and in 1957 were applied to describe the magnetic phase diagram of type-II superconductors by Alexei Alexeyevich Abrikosov. In 1935 Fritz London published a very closely related work on magnetic flux quantization in superconductors. London's fluxoid can also be viewed as a quantum vortex.
In continuum mechanics, wave turbulence is a set of nonlinear waves deviated far from thermal equilibrium. Such a state is usually accompanied by dissipation. It is either decaying turbulence or requires an external source of energy to sustain it. Examples are waves on a fluid surface excited by winds or ships, and waves in plasma excited by electromagnetic waves etc.
Injection locking and injection pulling are the frequency effects that can occur when a harmonic oscillator is disturbed by a second oscillator operating at a nearby frequency. When the coupling is strong enough and the frequencies near enough, the second oscillator can capture the first oscillator, causing it to have essentially identical frequency as the second oscillator. This is injection locking. When the second oscillator merely disturbs the first but does not capture it, the effect is called injection pulling. Injection locking and pulling effects are observed in numerous types of physical systems, however the terms are most often associated with electronic oscillators or laser resonators.
In the physics of coupled oscillators, antiresonance, by analogy with resonance, is a pronounced minimum in the amplitude of an oscillator at a particular frequency, accompanied by a large, abrupt shift in its oscillation phase. Such frequencies are known as the system's antiresonant frequencies, and at these frequencies the oscillation amplitude can drop to almost zero. Antiresonances are caused by destructive interference, for example between an external driving force and interaction with another oscillator.
In physics, nonlinear resonance is the occurrence of resonance in a nonlinear system. In nonlinear resonance the system behaviour – resonance frequencies and modes – depends on the amplitude of the oscillations, while for linear systems this is independent of amplitude. The mixing of modes in non-linear systems is termed resonant interaction.

Kapitza's pendulum or Kapitza pendulum is a rigid pendulum in which the pivot point vibrates in a vertical direction, up and down. It is named after Russian Nobel laureate physicist Pyotr Kapitza, who in 1951 developed a theory which successfully explains some of its unusual properties. The unique feature of the Kapitza pendulum is that the vibrating suspension can cause it to balance stably in an inverted position, with the bob above the suspension point. In the usual pendulum with a fixed suspension, the only stable equilibrium position is with the bob hanging below the suspension point; the inverted position is a point of unstable equilibrium, and the smallest perturbation moves the pendulum out of equilibrium. In nonlinear control theory the Kapitza pendulum is used as an example of a parametric oscillator that demonstrates the concept of "dynamic stabilization".

In condensed matter physics, a time crystal is a quantum system of particles whose lowest-energy state is one in which the particles are in repetitive motion. The system cannot lose energy to the environment and come to rest because it is already in its quantum ground state. Time crystals were first proposed theoretically by Frank Wilczek in 2012 as a time-based analogue to common crystals – whereas the atoms in crystals are arranged periodically in space, the atoms in a time crystal are arranged periodically in both space and time. Several different groups have demonstrated matter with stable periodic evolution in systems that are periodically driven. In terms of practical use, time crystals may one day be used as quantum computer memory.









