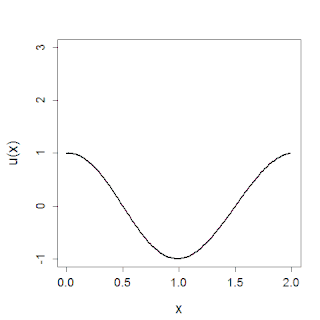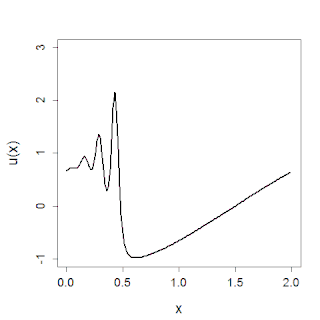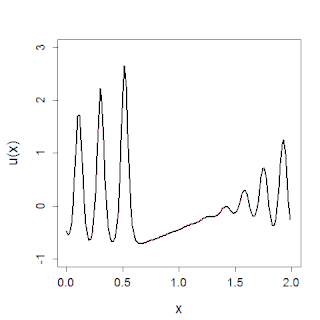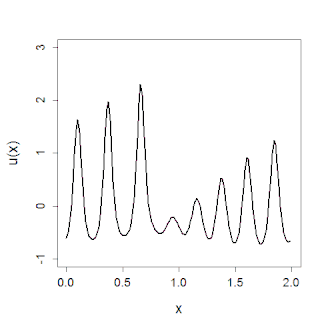
In mathematics, the Korteweg–De Vries (KdV) equation is a partial differential equation (PDE) which serves as a mathematical model of waves on shallow water surfaces. It is particularly notable as the prototypical example of an integrable PDE and exhibits many of the expected behaviors for an integrable PDE, such as a large number of explicit solutions, in particular soliton solutions, and an infinite number of conserved quantities, despite the nonlinearity which typically renders PDEs intractable. The KdV can be solved by the inverse scattering method (ISM). In fact, Gardner, Greene, Kruskal and Miura developed the classical inverse scattering method to solve the KdV equation.
In mathematics and physics, the inverse scattering problem is the problem of determining characteristics of an object, based on data of how it scatters incoming radiation or particles. It is the inverse problem to the direct scattering problem, which is to determine how radiation or particles are scattered based on the properties of the scatterer.
In mathematics and its applications, a Sturm–Liouville problem is a second-order linear ordinary differential equation of the form:
In mathematics, Bäcklund transforms or Bäcklund transformations relate partial differential equations and their solutions. They are an important tool in soliton theory and integrable systems. A Bäcklund transform is typically a system of first order partial differential equations relating two functions, and often depending on an additional parameter. It implies that the two functions separately satisfy partial differential equations, and each of the two functions is then said to be a Bäcklund transformation of the other.

Martin David Kruskal was an American mathematician and physicist. He made fundamental contributions in many areas of mathematics and science, ranging from plasma physics to general relativity and from nonlinear analysis to asymptotic analysis. His most celebrated contribution was in the theory of solitons.
In mathematics, integrability is a property of certain dynamical systems. While there are several distinct formal definitions, informally speaking, an integrable system is a dynamical system with sufficiently many conserved quantities, or first integrals, that its motion is confined to a submanifold of much smaller dimensionality than that of its phase space.

In mathematics and physics, the Kadomtsev–Petviashvili equation is a partial differential equation to describe nonlinear wave motion. Named after Boris Borisovich Kadomtsev and Vladimir Iosifovich Petviashvili, the KP equation is usually written as

In mathematics, the inverse scattering transform is a method that solves the initial value problem for a nonlinear partial differential equation using mathematical methods related to wave scattering. The direct scattering transform describes how a function scatters waves or generates bound-states. The inverse scattering transform uses wave scattering data to construct the function responsible for wave scattering. The direct and inverse scattering transforms are analogous to the direct and inverse Fourier transforms which are used to solve linear partial differential equations.
In mathematics, in the theory of integrable systems, a Lax pair is a pair of time-dependent matrices or operators that satisfy a corresponding differential equation, called the Lax equation. Lax pairs were introduced by Peter Lax to discuss solitons in continuous media. The inverse scattering transform makes use of the Lax equations to solve such systems.
In mathematics, the KdV hierarchy is an infinite sequence of partial differential equations which contains the Korteweg–de Vries equation.

In fluid dynamics, the Camassa–Holm equation is the integrable, dimensionless and non-linear partial differential equation
In quantum physics, the quantum inverse scattering method (QISM) or the algebraic Bethe ansatz is a method for solving integrable models in 1+1 dimensions, introduced by Leon Takhtajan and L. D. Faddeev in 1979.

Gerald Teschl is an Austrian mathematical physicist and professor of mathematics. He works in the area of mathematical physics; in particular direct and inverse spectral theory with application to completely integrable partial differential equations.
In mathematics, the Novikov–Veselov equation is a natural (2+1)-dimensional analogue of the Korteweg–de Vries (KdV) equation. Unlike another (2+1)-dimensional analogue of KdV, the Kadomtsev–Petviashvili equation, it is integrable via the inverse scattering transform for the 2-dimensional stationary Schrödinger equation. Similarly, the Korteweg–de Vries equation is integrable via the inverse scattering transform for the 1-dimensional Schrödinger equation. The equation is named after S.P. Novikov and A.P. Veselov who published it in Novikov & Veselov (1984).
Clifford Spear Gardner was an American mathematician specializing in applied mathematics.
The unnormalized modified Korteweg–de Vries (KdV) equation is an integrable nonlinear partial differential equation:
A fifth-order Korteweg–De Vries (KdV) equation is a nonlinear partial differential equation in 1+1 dimensions related to the Korteweg–De Vries equation. Fifth order KdV equations may be used to model dispersive phenomena such as plasma waves when the third-order contributions are small. The term may refer to equations of the form
The modified KdV–Burgers equation is a nonlinear partial differential equation
Integrable algorithms are numerical algorithms that rely on basic ideas from the mathematical theory of integrable systems.
The Schamel equation (S-equation) is a nonlinear partial differential equation of first order in time and third order in space. Similar to a Korteweg–De Vries equation (KdV), it describes the development of a localized, coherent wave structure that propagates in a nonlinear dispersive medium. It was first derived in 1973 by Hans Schamel to describe the effects of electron trapping in the trough of the potential of a solitary electrostatic wave structure travelling with ion acoustic speed in a two-component plasma. It now applies to various localized pulse dynamics such as:








