 | Look up eccentric or eccentricity in Wiktionary, the free dictionary. |
Eccentricity or eccentric may refer to:
 | This disambiguation page lists articles associated with the title Eccentricity. If an internal link led you here, you may wish to change the link to point directly to the intended article. |
In physics, an orbit is the gravitationally curved trajectory of an object, such as the trajectory of a planet around a star or a natural satellite around a planet. Normally, orbit refers to a regularly repeating trajectory, although it may also refer to a non-repeating trajectory. To a close approximation, planets and satellites follow elliptic orbits, with the center of mass being orbited at a focal point of the ellipse, as described by Kepler's laws of planetary motion.
Precession is a change in the orientation of the rotational axis of a rotating body. In an appropriate reference frame it can be defined as a change in the first Euler angle, whereas the third Euler angle defines the rotation itself. In other words, if the axis of rotation of a body is itself rotating about a second axis, that body is said to be precessing about the second axis. A motion in which the second Euler angle changes is called nutation. In physics, there are two types of precession: torque-free and torque-induced.
Orbital elements are the parameters required to uniquely identify a specific orbit. In celestial mechanics these elements are considered in two-body systems using a Kepler orbit. There are many different ways to mathematically describe the same orbit, but certain schemes, each consisting of a set of six parameters, are commonly used in astronomy and orbital mechanics.
Orbital mechanics or astrodynamics is the application of ballistics and celestial mechanics to the practical problems concerning the motion of rockets and other spacecraft. The motion of these objects is usually calculated from Newton's laws of motion and law of universal gravitation. Orbital mechanics is a core discipline within space-mission design and control.
Anomaly may refer to:
A geocentric orbit or Earth orbit involves any object orbiting the Earth, such as the Moon or artificial satellites. In 1997 NASA estimated there were approximately 2,465 artificial satellite payloads orbiting the Earth and 6,216 pieces of space debris as tracked by the Goddard Space Flight Center. Over 16,291 previously launched objects have decayed into the Earth's atmosphere.
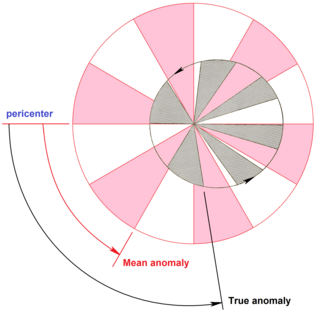
In celestial mechanics, the mean anomaly is the fraction of an elliptical orbit's period that has elapsed since the orbiting body passed periapsis, expressed as an angle which can be used in calculating the position of that body in the classical two-body problem. It is the angular distance from the pericenter which a fictitious body would have if it moved in a circular orbit, with constant speed, in the same orbital period as the actual body in its elliptical orbit.
In orbital mechanics, the eccentric anomaly is an angular parameter that defines the position of a body that is moving along an elliptic Kepler orbit. The eccentric anomaly is one of three angular parameters ("anomalies") that define a position along an orbit, the other two being the true anomaly and the mean anomaly.
In celestial mechanics, true anomaly is an angular parameter that defines the position of a body moving along a Keplerian orbit. It is the angle between the direction of periapsis and the current position of the body, as seen from the main focus of the ellipse.
In celestial mechanics, the eccentricity vector of a Kepler orbit is the dimensionless vector with direction pointing from apoapsis to periapsis and with magnitude equal to the orbit's scalar eccentricity. For Kepler orbits the eccentricity vector is a constant of motion. Its main use is in the analysis of almost circular orbits, as perturbing (non-Keplerian) forces on an actual orbit will cause the osculating eccentricity vector to change continuously. For the eccentricity and argument of periapsis parameters, eccentricity zero corresponds to a singularity. The magnitude of the eccentricity vector represents the eccentricity of the orbit. Note that the velocity and position vectors need to be relative to the inertial frame of the central body.
The argument of periapsis, symbolized as ω, is one of the orbital elements of an orbiting body. Parametrically, ω is the angle from the body's ascending node to its periapsis, measured in the direction of motion.
In celestial mechanics, the longitude of the periapsis, also called longitude of the pericenter, of an orbiting body is the longitude at which the periapsis would occur if the body's orbit inclination were zero. It is usually denoted ϖ.
In astrodynamics or celestial mechanics, a hyperbolic trajectory is the trajectory of any object around a central body with more than enough speed to escape the central object's gravitational pull. The name derives from the fact that according to Newtonian theory such an orbit has the shape of a hyperbola. In more technical terms this can be expressed by the condition that the orbital eccentricity is greater than one.
The orbital eccentricity of an astronomical object is a dimensionless parameter that determines the amount by which its orbit around another body deviates from a perfect circle. A value of 0 is a circular orbit, values between 0 and 1 form an elliptic orbit, 1 is a parabolic escape orbit, and greater than 1 is a hyperbola. The term derives its name from the parameters of conic sections, as every Kepler orbit is a conic section. It is normally used for the isolated two-body problem, but extensions exist for objects following a Klemperer rosette orbit through the galaxy.
Spacecraft flight dynamics is the application of mechanical dynamics to model how the external forces acting on a space vehicle or spacecraft determine its flight path. These forces are primarily of three types: propulsive force provided by the vehicle's engines; gravitational force exerted by the Earth and other celestial bodies; and aerodynamic lift and drag.
In classical geometry, a radius of a circle or sphere is any of the line segments from its center to its perimeter, and in more modern usage, it is also their length. The name comes from the Latin radius, meaning ray but also the spoke of a chariot wheel. The plural of radius can be either radii or the conventional English plural radiuses. The typical abbreviation and mathematical variable name for radius is r. By extension, the diameter d is defined as twice the radius:
In celestial mechanics, a Kepler orbit is the motion of one body relative to another, as an ellipse, parabola, or hyperbola, which forms a two-dimensional orbital plane in three-dimensional space. A Kepler orbit can also form a straight line. It considers only the point-like gravitational attraction of two bodies, neglecting perturbations due to gravitational interactions with other objects, atmospheric drag, solar radiation pressure, a non-spherical central body, and so on. It is thus said to be a solution of a special case of the two-body problem, known as the Kepler problem. As a theory in classical mechanics, it also does not take into account the effects of general relativity. Keplerian orbits can be parametrized into six orbital elements in various ways.
In geometry, the major axis of an ellipse is its longest diameter: a line segment that runs through the center and both foci, with ends at the widest points of the perimeter.
The position of the Sun in the sky is a function of both the time and the geographic location of observation on Earth's surface. As Earth orbits the Sun over the course of a year, the Sun appears to move with respect to the fixed stars on the celestial sphere, along a circular path called the ecliptic.
Most of the terms listed in Wikipedia glossaries are already defined and explained within Wikipedia itself. However, glossaries like this one are useful for looking up, comparing and reviewing large numbers of terms together. You can help enhance this page by adding new terms or writing definitions for existing ones.