
In 3D computer graphics, a voxel represents a value on a regular grid in three-dimensional space. As with pixels in a 2D bitmap, voxels themselves do not typically have their position explicitly encoded with their values. Instead, rendering systems infer the position of a voxel based upon its position relative to other voxels.
Bézier surfaces are a species of mathematical spline used in computer graphics, computer-aided design, and finite element modeling. As with Bézier curves, a Bézier surface is defined by a set of control points. Similar to interpolation in many respects, a key difference is that the surface does not, in general, pass through the central control points; rather, it is "stretched" toward them as though each were an attractive force. They are visually intuitive, and for many applications, mathematically convenient.

Solid modeling is a consistent set of principles for mathematical and computer modeling of three-dimensional shapes (solids). Solid modeling is distinguished from related areas of geometric modeling and computer graphics, such as 3D modeling, by its emphasis on physical fidelity. Together, the principles of geometric and solid modeling form the foundation of 3D-computer-aided design and in general support the creation, exchange, visualization, animation, interrogation, and annotation of digital models of physical objects.
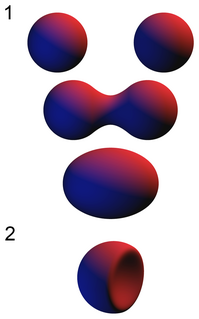
In computer graphics, metaballs are organic-looking n-dimensional isosurfaces, characterised by their ability to meld together when in close proximity to create single, contiguous objects.

Skeletal animation or rigging is a technique in computer animation in which a character is represented in two parts: a surface representation used to draw the character and a hierarchical set of interconnected parts, a virtual armature used to animate the mesh. While this technique is often used to animate humans and other organic figures, it only serves to make the animation process more intuitive, and the same technique can be used to control the deformation of any object—such as a door, a spoon, a building, or a galaxy. When the animated object is more general than, for example, a humanoid character, the set of "bones" may not be hierarchical or interconnected, but simply represent a higher-level description of the motion of the part of mesh it is influencing.

In 3D computer graphics and solid modeling, a polygon mesh is a collection of vertices, edges and faces that defines the shape of a polyhedral object. The faces usually consist of triangles, quadrilaterals (quads), or other simple convex polygons (n-gons), since this simplifies rendering, but may also be more generally composed of concave polygons, or even polygons with holes.

The Catmull–Clark algorithm is a technique used in 3D computer graphics to create curved surfaces by using subdivision surface modeling. It was devised by Edwin Catmull and Jim Clark in 1978 as a generalization of bi-cubic uniform B-spline surfaces to arbitrary topology.

The Facial Action Coding System (FACS) is a system to taxonomize human facial movements by their appearance on the face, based on a system originally developed by a Swedish anatomist named Carl-Herman Hjortsjö. It was later adopted by Paul Ekman and Wallace V. Friesen, and published in 1978. Ekman, Friesen, and Joseph C. Hager published a significant update to FACS in 2002. Movements of individual facial muscles are encoded by the FACS from slight different instant changes in facial appearance. It is a common standard to systematically categorize the physical expression of emotions, and it has proven useful to psychologists and to animators. Due to subjectivity and time consumption issues, the FACS has been established as a computed automated system that detects faces in videos, extracts the geometrical features of the faces, and then produces temporal profiles of each facial movement.

Geometry processing, or mesh processing, is an area of research that uses concepts from applied mathematics, computer science and engineering to design efficient algorithms for the acquisition, reconstruction, analysis, manipulation, simulation and transmission of complex 3D models. As the name implies, many of the concepts, data structures, and algorithms are directly analogous to signal processing and image processing. For example, where image smoothing might convolve an intensity signal with a blur kernel formed using the Laplace operator, geometric smoothing might be achieved by convolving a surface geometry with a blur kernel formed using the Laplace-Beltrami operator.

The orbicularis oculi is a muscle in the face that closes the eyelids. It arises from the nasal part of the frontal bone, from the frontal process of the maxilla in front of the lacrimal groove, and from the anterior surface and borders of a short fibrous band, the medial palpebral ligament.

In computer graphics, a triangulated irregular network (TIN) is a representation of a continuous surface consisting entirely of triangular facets, used mainly as Discrete Global Grid in primary elevation modeling.
Computer facial animation is primarily an area of computer graphics that encapsulates methods and techniques for generating and animating images or models of a character face. The character can be a human, a humanoid, an animal, a legendary creature or character, etc. Due to its subject and output type, it is also related to many other scientific and artistic fields from psychology to traditional animation. The importance of human faces in verbal and non-verbal communication and advances in computer graphics hardware and software have caused considerable scientific, technological, and artistic interests in computer facial animation.

Mesh generation is the practice of creating a mesh, a subdivision of a continuous geometric space into discrete geometric and topological cells. Often these cells form a simplicial complex. Usually the cells partition the geometric input domain. Mesh cells are used as discrete local approximations of the larger domain. Meshes are created by computer algorithms, often with human guidance through a GUI, depending on the complexity of the domain and the type of mesh desired. A typical goal is to create a mesh that accurately captures the input domain geometry, with high-quality (well-shaped) cells, and without so many cells as to make subsequent calculations intractable. The mesh should also be fine in areas that are important for the subsequent calculations.

Pixologic ZBrush is a digital sculpting tool that combines 3D/2.5D modeling, texturing and painting. It uses a proprietary "pixol" technology which stores lighting, color, material, orientation and depth information for the points making up all objects on the screen. The main difference between ZBrush and more traditional modeling packages is that it is more akin to traditional sculpting.

Digital sculpting, also known as sculpt modeling or 3D sculpting, is the use of software that offers tools to push, pull, smooth, grab, pinch or otherwise manipulate a digital object as if it were made of a real-life substance such as clay.
In mesh generation, Delaunay refinement are algorithms for mesh generation based on the principle of adding Steiner points to the geometry of an input to be meshed, in a way that causes the Delaunay triangulation or constrained Delaunay triangulation of the augmented input to meet the quality requirements of the meshing application. Delaunay refinement methods include methods by Chew and by Ruppert.
Image-based meshing is the automated process of creating computer models for computational fluid dynamics (CFD) and finite element analysis (FEA) from 3D image data. Although a wide range of mesh generation techniques are currently available, these were usually developed to generate models from computer-aided design (CAD), and therefore have difficulties meshing from 3D imaging data.

In 3D computer graphics, 3D modeling is the process of developing a mathematical coordinate-based representation of any surface of an object in three dimensions via specialized software by manipulating edges, vertices, and polygons in a simulated 3D space.
3D-Coat is a commercial digital sculpting program from Pilgway designed to create free-form organic and hard surfaced 3D models from scratch, with tools which enable users to sculpt, add polygonal topology, create UV maps, texture the resulting models with natural painting tools, and render static images or animated "turntable" movies.

3D reconstruction from multiple images is the creation of three-dimensional models from a set of images. It is the reverse process of obtaining 2D images from 3D scenes.















