
Maxwell's equations, or Maxwell–Heaviside equations, are a set of coupled partial differential equations that, together with the Lorentz force law, form the foundation of classical electromagnetism, classical optics, and electric circuits. The equations provide a mathematical model for electric, optical, and radio technologies, such as power generation, electric motors, wireless communication, lenses, radar etc. They describe how electric and magnetic fields are generated by charges, currents, and changes of the fields. The equations are named after the physicist and mathematician James Clerk Maxwell, who, in 1861 and 1862, published an early form of the equations that included the Lorentz force law. Maxwell first used the equations to propose that light is an electromagnetic phenomenon. The modern form of the equations in their most common formulation is credited to Oliver Heaviside.
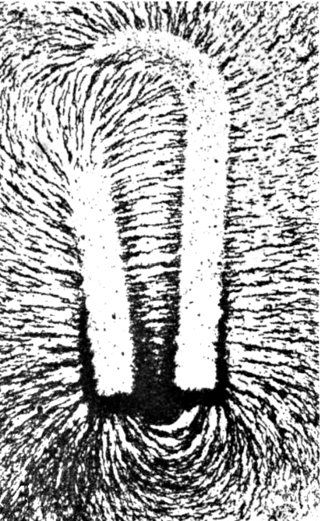
A magnetic field is a vector field that describes the magnetic influence on moving electric charges, electric currents, and magnetic materials. A moving charge in a magnetic field experiences a force perpendicular to its own velocity and to the magnetic field. A permanent magnet's magnetic field pulls on ferromagnetic materials such as iron, and attracts or repels other magnets. In addition, a nonuniform magnetic field exerts minuscule forces on "nonmagnetic" materials by three other magnetic effects: paramagnetism, diamagnetism, and antiferromagnetism, although these forces are usually so small they can only be detected by laboratory equipment. Magnetic fields surround magnetized materials, and are created by electric currents such as those used in electromagnets, and by electric fields varying in time. Since both strength and direction of a magnetic field may vary with location, it is described mathematically by a function assigning a vector to each point of space, called a vector field.

In mathematics and physics, Laplace's equation is a second-order partial differential equation named after Pierre-Simon Laplace, who first studied its properties. This is often written as

An electric field is the physical field that surrounds electrically charged particles and exerts force on all other charged particles in the field, either attracting or repelling them. It also refers to the physical field for a system of charged particles. Electric fields originate from electric charges and time-varying electric currents. Electric fields and magnetic fields are both manifestations of the electromagnetic field, one of the four fundamental interactions of nature.

In physics and electromagnetism, Gauss's law, also known as Gauss's flux theorem, is a law relating the distribution of electric charge to the resulting electric field. In its integral form, it states that the flux of the electric field out of an arbitrary closed surface is proportional to the electric charge enclosed by the surface, irrespective of how that charge is distributed. Even though the law alone is insufficient to determine the electric field across a surface enclosing any charge distribution, this may be possible in cases where symmetry mandates uniformity of the field. Where no such symmetry exists, Gauss's law can be used in its differential form, which states that the divergence of the electric field is proportional to the local density of charge.

In mathematics and physics, the heat equation is a certain partial differential equation. Solutions of the heat equation are sometimes known as caloric functions. The theory of the heat equation was first developed by Joseph Fourier in 1822 for the purpose of modeling how a quantity such as heat diffuses through a given region.

In classical electromagnetism, Ampère's circuital law relates the integrated magnetic field around a closed loop to the electric current passing through the loop. James Clerk Maxwell derived it using hydrodynamics in his 1861 published paper "On Physical Lines of Force" In 1865 he generalized the equation to apply to time-varying currents by adding the displacement current term, resulting in the modern form of the law, sometimes called the Ampère–Maxwell law, which is one of Maxwell's equations which form the basis of classical electromagnetism.
In electromagnetics, an evanescent field, or evanescent wave, is an oscillating electric and/or magnetic field that does not propagate as an electromagnetic wave but whose energy is spatially concentrated in the vicinity of the source. Even when there is a propagating electromagnetic wave produced, one can still identify as an evanescent field the component of the electric or magnetic field that cannot be attributed to the propagating wave observed at a distance of many wavelengths.

A Halbach array is a special arrangement of permanent magnets that augments the magnetic field on one side of the array while cancelling the field to near zero on the other side. This is achieved by having a spatially rotating pattern of magnetisation.

An electromagnetic four-potential is a relativistic vector function from which the electromagnetic field can be derived. It combines both an electric scalar potential and a magnetic vector potential into a single four-vector.
In classical electromagnetism, magnetic vector potential is the vector quantity defined so that its curl is equal to the magnetic field: . Together with the electric potential φ, the magnetic vector potential can be used to specify the electric field E as well. Therefore, many equations of electromagnetism can be written either in terms of the fields E and B, or equivalently in terms of the potentials φ and A. In more advanced theories such as quantum mechanics, most equations use potentials rather than fields.
The electric-field integral equation is a relationship that allows the calculation of an electric field (E) generated by an electric current distribution (J).
In classical electromagnetism, reciprocity refers to a variety of related theorems involving the interchange of time-harmonic electric current densities (sources) and the resulting electromagnetic fields in Maxwell's equations for time-invariant linear media under certain constraints. Reciprocity is closely related to the concept of symmetric operators from linear algebra, applied to electromagnetism.
The electromagnetic wave equation is a second-order partial differential equation that describes the propagation of electromagnetic waves through a medium or in a vacuum. It is a three-dimensional form of the wave equation. The homogeneous form of the equation, written in terms of either the electric field E or the magnetic field B, takes the form:
The method of image charges is a basic problem-solving tool in electrostatics. The name originates from the replacement of certain elements in the original layout with imaginary charges, which replicates the boundary conditions of the problem.
The uniqueness theorem for Poisson's equation states that, for a large class of boundary conditions, the equation may have many solutions, but the gradient of every solution is the same. In the case of electrostatics, this means that there is a unique electric field derived from a potential function satisfying Poisson's equation under the boundary conditions.

The London equations, developed by brothers Fritz and Heinz London in 1935, are constitutive relations for a superconductor relating its superconducting current to electromagnetic fields in and around it. Whereas Ohm's law is the simplest constitutive relation for an ordinary conductor, the London equations are the simplest meaningful description of superconducting phenomena, and form the genesis of almost any modern introductory text on the subject. A major triumph of the equations is their ability to explain the Meissner effect, wherein a material exponentially expels all internal magnetic fields as it crosses the superconducting threshold.
The Transition Matrix Method is a computational technique of light scattering by nonspherical particles originally formulated by Peter C. Waterman (1928–2012) in 1965. The technique is also known as null field method and extended boundary condition method (EBCM). In the method, matrix elements are obtained by matching boundary conditions for solutions of Maxwell equations. It has been greatly extended to incorporate diverse types of linear media occupying the region enclosing the scatterer.
Lagrangian field theory is a formalism in classical field theory. It is the field-theoretic analogue of Lagrangian mechanics. Lagrangian mechanics is used to analyze the motion of a system of discrete particles each with a finite number of degrees of freedom. Lagrangian field theory applies to continua and fields, which have an infinite number of degrees of freedom.
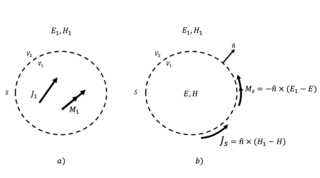
In electromagnetism, surface equivalence principle or surface equivalence theorem relates an arbitrary current distribution within an imaginary closed surface with an equivalent source on the surface. It is also known as field equivalence principle, Huygens' equivalence principle or simply as the equivalence principle. Being a more rigorous reformulation of the Huygens–Fresnel principle, it is often used to simplify the analysis of radiating structures such as antennas.












